どうも、木村(@kimu3_slime)です。
小学校の算数で、筆算や計算ミスに悩み、苦手意識を覚えた人は少なくないのではないでしょうか。
僕は大学以降でも数学を学び続けましたが、手計算をするときに、筆算を使っていないことに気づきました。
じゃあどうやって計算するかといえば、途中式を使って工夫して計算するのです。中学の数学の知識が必要になりますが、こちらの方が工夫が生まれて面白いし、致命的なミスが減ります。そのやり方を、一部紹介します。
繰り下がりを含む引き算の計算
\(606-259\)という、繰り下がりを含む引き算の値を求めたいとしましょう。
筆算では、次の画像のように上の位から10を借りてきて計算するようです。
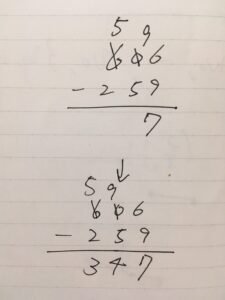
正直、上の位を書き換えるというやり方は、Google検索して知りました。昔僕が筆算していたときは、脳内で右から\(9+7=16\)だから\(7\)、\(10-5\)で\(1\)使ってたから\(4\)、\(6-2\)で\(1\)使ってたから\(3\)、と計算していました。
こうして書いていても、繰り下がりを含む多くの暗算を行っているので、間違いやすそうです。
では、途中式を使った計算法を紹介しましょう。
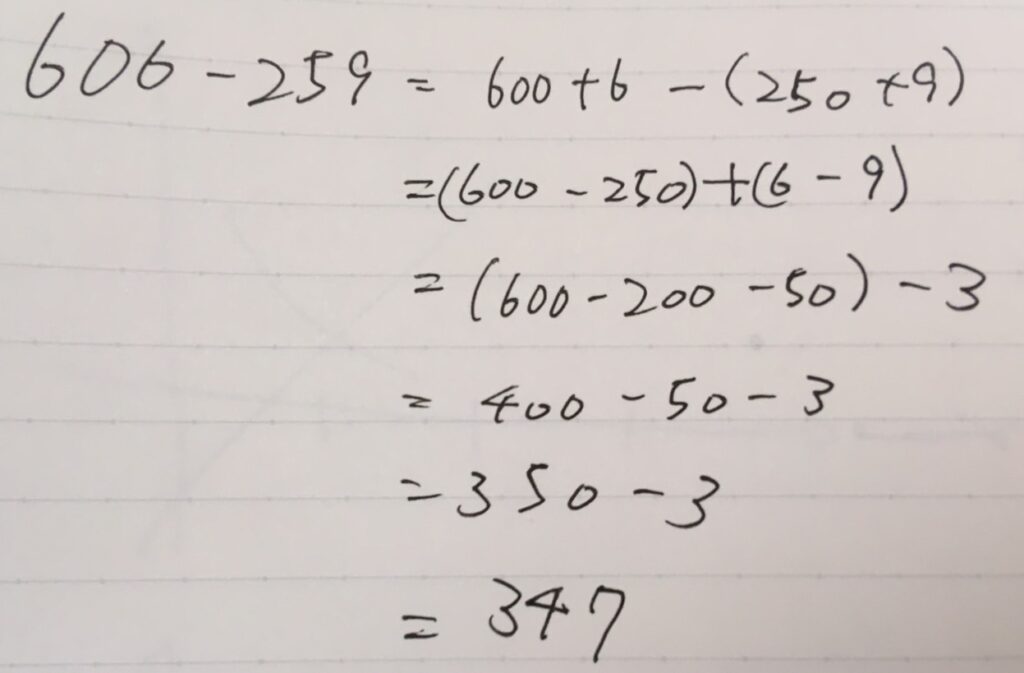
基本的な方針は、桁ごとの分解です。\(606\)は\(600\)くらい、\(259\)は\(250\)くらい、およそくらいの数だなと見積もっていきます。(どんな見積もり方でもOKです。見返したら、\(259=260-1\)の方が計算しやすいですね。)
\(606=600+6\)、\(259=250+9\)と分解します。\(259\)というまとまりを引くのですから、\(-259=-(250+9)\)と変形され、\(-259=-250+9\)でないことに注意しましょう。
足し算と引き算には交換法則があるので、順番を入れ替えて計算できます。\(600-250\)、\(6-9\)は比較的簡単ですね。マイナスの計算の知識は必要になりますが、一桁なので安心です。
\(60-25=35\)と暗算できるなら\(600-250=350\)とそのまま計算して良いです。不安ならば、画像に示したように、\(600-200-50\)とさらに分解すれば、これも1桁の計算になります。
途中式を使った計算は、結局その中身は筆算と同じです。というか、筆算は途中式を使って計算を、システマティックにしたものと言えます。
一見すると、途中式を使った計算は、行数が多く、それによって計算ミスを多発するように見えます。これは丁寧に書いたからにすぎません。
僕が暗算でするときは、\(606-259=340+6+1=347\)くらいでやってます。逆に言えば、筆算は、本質的に複数の式の暗算を同時に行っているのです。そりゃ間違えます。
そして間違えたとしてどこで間違えたのかわかりにくいのが、筆算のデメリットだと思っています。途中式による計算では、1行ずつ簡単な等式変形しかしていないので、1ステップごとにミスがないか確認できます。仮にミスがあったとしても、おおざっぱな値を見積もっているので、(筆算では起こりうる桁ズレのような)大きなズレが起こりにくいです。
小数のかけ算
ミスが起こりがちなのが、小数の計算です。\(0.43 \times 2.5\)を計算してみましょう。
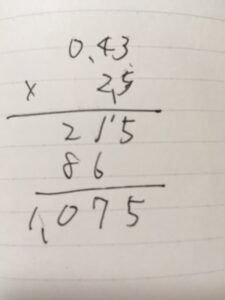
小数点がない数と同じようにかけ算を筆算で計算して、最後に小数点\(.\)がずれている分だけずらせば、答えが得られますよ、という手順です。
正直、計算手順は知っていますが、なぜそれで答えになっているか、説明できる人はどれくらいいるのでしょうか。僕は当時は理解していないまま、計算していた気がします。
途中式を書いて計算しましょう。
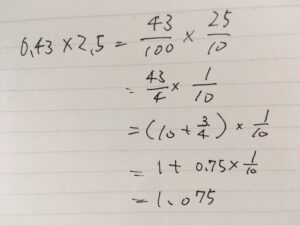
最初に行うのは、数の大きさの見積もりです。\(10,100,1000\)などを基準にして、\(0.1=1/10,0.01=1/100\)と分数で言い換えます。
一度分数で言い換えたら、分数の計算ができて、ここでは\(25,100\)が約分できました。この問題は\(2.5\)のおかげで、機械的な筆算に比べ、計算が楽になっているのです。
\(43/4\)を、\(10+3/4\)と捉えました。小学校ではこれは帯分数\(10\frac{3}{4}\)として表記するよう習うかもしれませんが、かけ算\(10\times \frac{3}{4}\)と紛らわしいのでやめたほうが良いと思います。およその数、整数部分を捉えたいなら、ちゃんと\(10+3/4\)と書けば良いのです。
最後の計算で、分数を小数に戻しています。分数・小数の相互の変換は、慣れないと大変かもしれません。この点では、筆算の方が単純です。
しかし、中学校以降の数学・科学においては、(小数でなく)分数を使った立式、数式処理が基本となります。それは誤差を伴わないためです。例えば円周率を\(3.14\)でなく\(\pi \)で扱って、最後の段階で小数で求めたければ近似値を使うのです。
途中式を使った計算で、小数・分数の相互関係に慣れておけば、小数・分数が表す「およその数」がイメージでき、桁ズレのようなありえない結果を導くケースを減らせるでしょう。
割り算の計算
最後に割り算の例として、\(99\div 24\)を計算してみましょう。
筆算だと、次のようにいくつかの計算を試す必要があるかと思います。
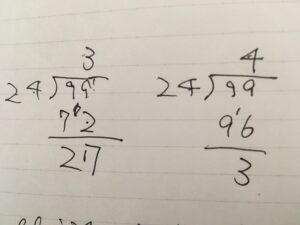
一発で商を立てられるのは、暗算に十分馴染んだ人ではないでしょうか。
途中式を使って計算してみましょう。
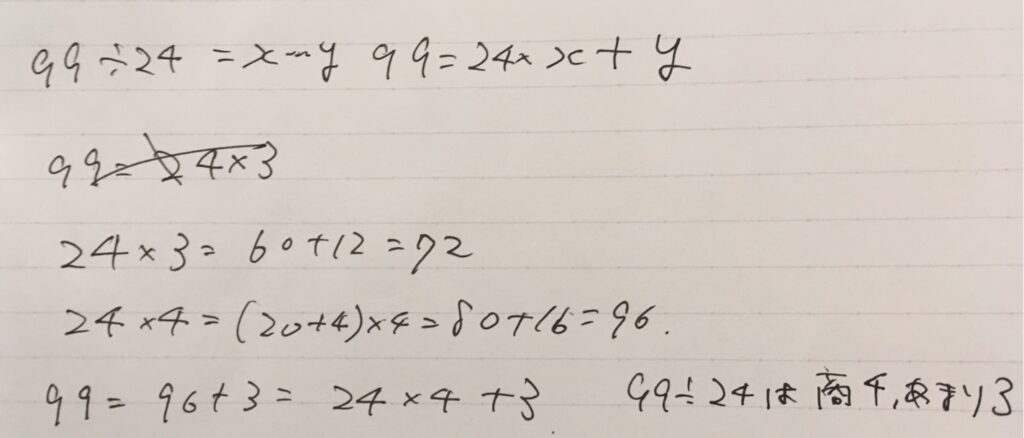
まず(整数の)割り算をするということは、\(99=24\times x +y\)となる整数\(x,y\)を求めることでることを確認しておきましょう。あまり\(y\)は、割る数\(24\)より小さい整数です。
まずは、\(24\)の倍数をチェックしていく必要があります。検討をつけて、\(3,4\)倍を計算して\(99\)に近いかどうか考えましょう。
\(24 \times 4=96\)は\(99\)に近いので、\(99\)を\(24\)の倍数と残った部分に分ければ、割り算の答えが求められました。
整数の割り算の定義、\(a\div b\)の商が\(q\)、あまりが\(r\)とは、\(a=qb+r\)が成り立つことです。これは、除法の原理と呼ばれるものです。
参考:整数の除法、割り切れる・約数b|a、最大公約数gcdとは?
算数の時間にこれを習った記憶はありませんが、割り算とはそういう意味だったのです。割ることの意味をきちんと捉えることは、中学校以降で整数の性質、多項式の割り算を学ぶときにつながります。
また、整数の範囲でなく実数の範囲で割り算を考えれば、\(99\div 24 =\frac{33}{8}\)です。割り算であまりを考えたり、分数で計算したりよくわからなくなってしまう理由は、「割り算とは何か」がわかっていないことに一因があるでしょう。
以上、小学校で扱う計算を例に、筆算ではなく途中式を書いて計算する方法を紹介してきました。
確かに、筆算は慣れれば計算が速く、どんな問題も(正しく遂行できれば)機械的に答えが求められるというメリットがあります。
しかし、それだけが数の計算方法ではありません。おおざっぱに数を見積もり、途中式を書いてゆっくり地道に答えを求める方法もあるのです。
僕は小学校では筆算が苦手ではなかったので、算数には苦しみませんでした。でも、筆算が苦手で、たくさんやらされて算数自体が面白くないと思った人は少なくないでしょう。過剰な計算を強いられて、算数や数学を嫌いになってしまうのはもったいないことだと思います。
この記事を通して、単なる計算でもいろいろな解き方があること、筆算が苦手に感じても大丈夫ということが伝えられたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
すばる舎 (2016-04-21T00:00:00.000Z)
¥1,030
すばる舎 (2015-01-25T00:00:00.000Z)
¥1,091