グラフ理論における木とは、判定法、オイラーの公式

どうも、木村（@kimu3_slime）です。

今回は、グラフ理論における木とは何か、その判定法、オイラーの公式を紹介します。

木とはなにか
木の判定法
こちらもおすすめ

木とはなにか

木とは、グラフ（点と辺の集まり）の一種で、木のような形をしたものです。とはいえ、木のような形、というのはきちんとした定義にはなりません。

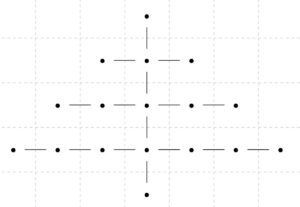
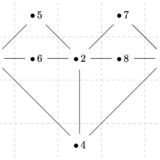
グラフが木（tree）であるとは、連結であり、サイクル（単純な閉経路）を持たないことです。

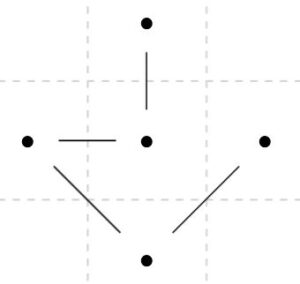
確かに、上のグラフや次のグラフは、連結であり、サイクルを持たないので、木となっています。

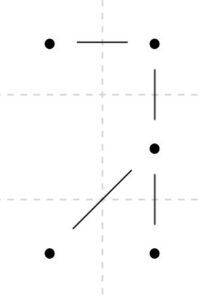
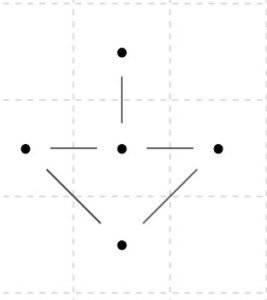
次のグラフは木ではありません。三角形部分がサイクルとなっています。

木は、パソコンのフォルダ（ディレクトリツリー）のような情報の階層構造（ツリー構造）を表したり、文法や記号の規則を調べるために使われます（構文解析）。

また、一般にはグラフはサイクルを含みますが、その頂点を残したまま辺を部分的に選んで得られる木（全域木）を見つける問題が考えられます。これは使っている辺を減らしながらすべての頂点に情報や電気を伝播させられるので、ネットワークの効率化になりますね。これは別記事にて紹介予定。

木の判定法

木はサイクルを含まないグラフと定義しましたが、サイクルを全く含まないことを見分けるのは、一般には簡単ではないでしょう。「存在しない」ことを示すには、原理的には「すべての」チェックが必要で、手間がかかります。

そこで、次のようないくつかの判定条件、特徴づけが知られています。

グラフ\(G=(V,E)\)について、次の条件は同値である。

\(G\)は木である。
経路の一意性：任意の\(v,w\in V\)に対し、端点が\(v,w\)である単純経路が一意に存在する。
最小の連結グラフ：\(G\)は連結であり、どの辺を削っても非連結なグラフになる。
サイクルを持たない最大のグラフ：\(G\)はサイクルを含まず、\(G\)にどんな新たな1つの辺を加えてもそれはサイクルを持つ。
オイラーの公式（Euler’s formula）：\(G\)は連結であり、\(\mathrm{card}(V)=\mathrm{card}(E) +1\)。\(\mathrm{card}(A)\)は集合の要素数。

まずは、これが正しいのかどうか、具体例を観察してみましょう。

2.経路の一意性について。同一の2頂点に対し、2つの異なる経路が作れたとすると、サイクルを持ってしまいますね。

3.最小の連結グラフ。確かに、どの辺を削っても、非連結なグラフになってしまいます。

4.サイクルを持たない最大のグラフ。確かに、このグラフでは持っていない辺を新たに加えると、その部分にサイクルができてしまいます。

5.オイラーの公式。頂点数と辺の数を数えます。\(\mathrm{card}(V)=5\)で、\(\mathrm{card}(E)=4\)で、\(\mathrm{card}(V)=\mathrm{card}(E) +1\)は確かに成り立っていますね。

木の判定条件の証明には、端点と呼ばれる頂点に注目します。

グラフの頂点\(v\)が端点（end-vertex）、または葉である（leaf）とは、その次数が1である\(\mathrm{deg}(v)=1\)ことです。木の端っこの点を葉に見立てているわけですね。

端点の補題（end-vertex lemma）

2つ以上の頂点を持つ木は、2つ以上の端点を持つ。

木成長の補題（tree-growing lemma）

グラフ\(G\)、その端点\(v\)について、次の2条件は同値。

\(G\)は木である。\(G\)から\(v\)と\(v\)を含む辺を除いたグラフは、木である。

どちらも、今まで見てきた例では、確かに成り立っていそうです。端点が\(0,1\)個のグラフを考えると、必ずサイクルを持つようなグラフになってしまいます。

木成長の補題は、端点を含む辺は、縮めていっても本質的に木であることは変わらないということです。

証明は「離散数学への招待〈上〉」を参照してください。

これらを使って、木の判定条件の証明を簡単に紹介しましょう。

基本的な方針は、頂点の数に関する数学的帰納法です。頂点数が\(1\)のときは、確かにすべてが成り立っています。以降では\(2\)頂点以上のケースを考えるので、補題が使えます。

まず、1.を仮定して2,3,4,5を導きます。端点の補題より2つ以上の端点がありますが、そのひとつを\(v\)とします。\(v\)には唯一の隣接する頂点があるので、それを\(w\)とします。木成長の補題より、\(G\)から\(v\)と\(v\)を含む辺を除いたグラフ\(G^{\prime }\)は、木です。帰納法の仮定より、\(G^{\prime}\)については2,3,4,5が満たされています。

2. について。\(G^{\prime}\)において経路は一意で、\(v,w\)の経路も一意なので、\(G\)の経路は一意となります。3.について。」 \(G^{\prime}\)は最小の連結グラフで、\(G\)では辺\(\{v,w\}\)を除けば\(v\)は孤立するので、\(G\)は最小の連結グラフです。4.について。\(G^{\prime}\)がサイクルを持たない最大のグラフで、\(v\)をつなげることでサイクルは増えないので（\(v\)は端点）、\(G\)はサイクルを持たない最大のグラフとなります。5.について。\(\mathrm{card}(V(G^{\prime}))=\mathrm{card}(G^{\prime})) +1\)が成り立ちますが、\(G\)はそれに頂点と辺を1つずつ加えたものなので、等式は保たれます。

2.から1.を示します。サイクルが存在したとしましょう。サイクルの始点を\(v_0\)、内部頂点を\(v_1\)とすると、サイクルを\(v_0\)から\(v_1\)、\(v_1\)から\(v_0\)と2つの異なる単純経路に分割できます。2頂点に異なる経路が存在することになり、矛盾です。

3.から1.を示します。サイクルが存在したとしましょう。サイクルの始点に隣り合う辺をひとつ減らしたグラフを考えても、頂点をつなぐ経路自体は保たれ、そのグラフは連結になります。これは仮定に反するので矛盾です。

4.から1.を示します。\(G\)はサイクルを持たないので、残りは連結であることについて。頂点\(v,w \in V(G)\)を任意に選びます。\(\{v,w\} \in E(G)\)のときは、それがそのまま経路になります。\(\{v,w\} \not \in E(G)\)のとき、その辺を加えたグラフはサイクルを持ちます。そのサイクルから\(\{v,w\}\)を除けば、\(G\)における\(v,w\)をつなぐ経路が存在することになり、連結であることが示せました。

5.から1.を示します。頂点数が\(2\)以上のとき、\(\mathrm{card}(V_k)=\mathrm{card}(E_k) +1\)が成り立つ連結なグラフ\(G_k=(V_k,E_k)\)を考えましょう。握手の補題\(\sum_{v\in V}\mathrm{deg}(v) = 2 \mathrm{card}(E)\)より、\(\sum_{v\in V_k}\mathrm{deg}(v)= 2\mathrm{card}(V_k)-2\)です。\(G_k\)は連結なので、頂点の次数は\(1\)以上であり、すべての頂点の次数は\(2\)以上であるわけではありません（仮にそうだとすると、一個前の等式に矛盾）。したがって、次数\(1\)の頂点、すなわち端点\(v\)が存在します。\(G_k\)から頂点\(v\)と隣接する辺を除いたグラフ\(G_{k}^{\prime}\)を考えると、\(G_{k}^{\prime}\)は連結であり、頂点と辺が1つ減ったので\(\mathrm{card}(G_{k}^{\prime})=\mathrm{card}(G_{k}^{\prime}) +1\)が成り立ちます。よって、帰納法の仮定より\(G_{k}^{\prime}\)は木で、木成長の補題より\(G_k\)は木であるとわかりました。

以上、グラフ理論における木とは何か、その判定法、オイラーの公式を紹介しました。

特に、頂点と辺の数に関するオイラーの公式で判別できるのは便利ですね。これは平面グラフにおけるオイラーの公式として一般化されます。別記事で紹介予定。

木、すなわちサイクルを持たない連結グラフは、経路と同様にグラフの基本的なパーツとして見ることができます。端点を使った議論も強力で、扱いやすそうですね。

木村すらいむ（@kimu3_slime）でした。ではでは。