どうも、木村(@kimu3_slime)です。
今回は、グラフ理論における一筆書きができる条件、オイラーグラフについて紹介します。
オイラーグラフとは
一筆書きができる条件は、グラフ理論の起源ともなった問題です。
ヨーロッパのケーニヒスベルクという土地に、次の図のような橋がかかっていました。
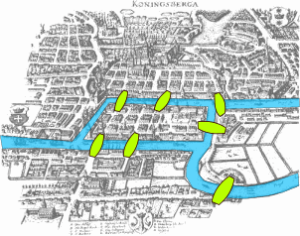
画像引用:The problem of the Seven Bridges of Königsberg. – Bogdan Giuşcă
同じ橋を二度通らずに、すべての橋を渡り切ってもとの場所に戻ってくることはできるでしょうか? これはケーニヒスベルクの橋の問題と呼ばれています。
一筆書きの可能性は、グラフ理論では経路を使って次のように定式化されます。
グラフのすべての頂点と辺を含み、辺の重複がない閉経路を、閉オイラー経路(closed Eulerian tour)と呼びます。そして、閉オイラー経路が存在するようなグラフを、オイラーグラフ(Eulerian graph)と呼びます。
より一般に、始点と終点が一致しなくても良いケース、グラフのすべての頂点と辺を含み辺の重複がない閉経路を、半オイラー経路(semi-Eulerian tour)と呼びます。半オイラー経路を持ち、オイラー経路を持たないグラフを半オイラーグラフ(semi-Eulerian graph)と呼びます。
具体的に考えていきましょう。

上のグラフにおいて、経路\((1,\{1,2\},2,\{2,3\},3,\{3,4\},4,\{4,1\},1)\)は、すべての辺を含んでいるので、オイラー経路です。つまり、このグラフはオイラーグラフです。
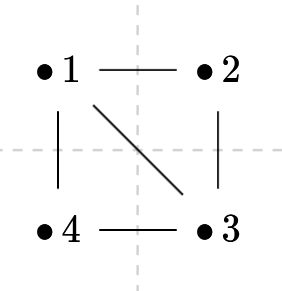
辺をひとつ加えたグラフはどうでしょうか。辺を省略して書くと、\((1,2,3,1,4,3)\)という経路は半オイラー経路です。
しかし、オイラーグラフではありません。奇数次数の頂点\(1,3\)に注目します。例えば\((1,3,2)\)のように\(3\)を通り抜ける経路を考えると、必ず隣接する辺2つを利用します。奇数次数の頂点を出発点としても、考える経路は終点と一致しなければならないので、行きと帰りで次数が2生まれます。したがって、奇数頂点に隣接する辺を使い切る経路は存在せず、オイラー経路は存在しません。
すなわち、このグラフは半オイラーグラフです。(半)オイラー経路の定義においては、辺の重複は許されませんが、同じ頂点を2回通ってもOKです。

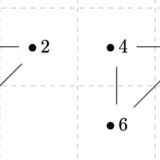
もうひとつ辺を足したグラフを考えます。奇数次数の頂点が存在するので、さきほどの議論と同様にして、オイラーグラフではありません。
さらに、半オイラーグラフでもありません。仮に、奇数次数の頂点\(v_1,v_2\)を始点と終点とする半オイラー経路が存在したとしましょう(背理法)。このグラフでは、\(v_1,v_2\)以外の奇数次数の頂点が存在します。オイラー経路の定義により、その頂点を通り抜けるので次数は偶数となるはずですが、実際には奇数次数であり矛盾します。
一筆書きができる条件
ここまでの状況を見ると、奇数次数の頂点が一筆書きには悪い性質を持っていそうです。実際には、次のことが示せます。
\(G\)を任意のグラフとする。
\(G\)がオイラーグラフであることは、連結であり、奇数次数の頂点が存在しないこと(すべての頂点が偶数次数であること)と同値。
\(G\)が半オイラーグラフであることは、連結であり、奇数次数の頂点が2つであることと同値。
この主張が正しそうか考えるために、オイラーグラフに頂点・辺を加えて変化させてみましょう。


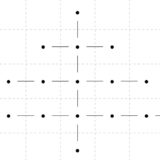
偶数次数の頂点を加えても、オイラーグラフであることには変わりません。
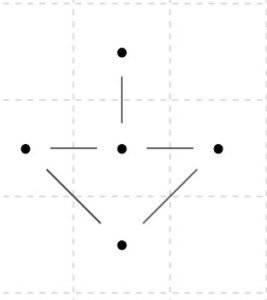
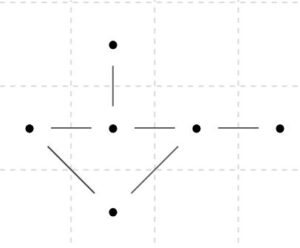
奇数次数であるように頂点、辺を加えると、オイラーグラフではなく、半オイラーグラフになりました。さらに奇数次数の頂点を増やせば、半オイラーグラフですらなくなりましたね。
では、証明しましょう。
\(G\)がオイラーグラフであると仮定します。オイラー経路\(P=(v_0,e_1,v_1,\dots,e_T,v_0)\)は、すべての頂点を通る経路なので、\(G\)は連結です。内部頂点\(v_{i}\)を通る部分経路\((v_{i-1},e_i,v_{i},e_{i+1},v_{i+1})\)に注目すると、\(v_{i}\)の次数は2ずつ増えます。\(P\)はすべての辺を通る経路なので、\(v_{i}\)は2を足していったもの、偶数となります。端点\(v_0\)については、内部頂点として現れるケースでは次数が2ずつ増えます。また、出発と到着において2つ辺が増えるので、結果として\(v_0\)の次数も偶数です。よって、すべての頂点の次数が偶数次数とわかました。
逆に、\(G\)を連結で、すべての頂点の次数が偶数と仮定しましょう。辺の重複がない最長の経路を、\(P=(v_0,e_1,v_1,\dots,e_T,v_T)\)と表しましょう(グラフの辺は有限個であり、辺を重複なく通るので、経路の長さは有限となります)。この経路は、すべての辺を含みます(仮に含まない辺があったとすると、連結性に反する)。したがって、\(P\)はすべての頂点を含んでいます。ここで、\(v_0 =v_T\)となります。\(v_0 \neq v_T\)と仮定すると、さきほどまでの議論から内部頂点としては次数が偶数ずつしか増えず、始点と終点で\(v_0,v_T\)が奇数次数の頂点となり、すべての頂点が偶数次数という仮定に矛盾するので。
さらに、\(P\)はオイラー経路であることが示せます。仮にオイラー経路でなかったとしましょう。すると、\(P\)に含まれない辺\(e\)、頂点\(w\)で、\(e= \{w,v_i\}\)であるようなものが存在します(\(G\)は連結なので)。\(P\)を使って、\(Q=(w,e,v_i,\dots,v_T,e_1,v_0,\dots,v_i)\)という経路を考えると、\(Q\)の長さは\(P\)より長くなり、\(P\)が最長経路であることに矛盾します。よって、\(P\)がオイラー閉経路であること、\(G\)がオイラーグラフであることが示せました。
\(G\)を半オイラーグラフと仮定します。半オイラー経路\(P=(v_0,e_1,v_1,\dots,e_T,v_T)\)は、すべての頂点を通る経路なので、\(G\)は連結です。\(v_0,v_T\)をつなぐような、\((v_0,e,w,e^{\prime},v_T)\)が経路となるような頂点\(w\)、辺\(e,e^{\prime}\)を加えたグラフ\(G_1\)を考えましょう。\(G_1\)はさきほどの\(P\)に\((v_0,e,w,e,v_T)\)をつなげた経路を考えれば、オイラーグラフです。したがって、示したことにより\(G_1\)のすべての頂点は偶数次数となります。そして、そこから頂点\(w\)、辺\(e,e^{\prime}\)を除くと、\(v_0,v_T\)の次数が1ずつ引かれ、奇数次数の頂点が2つであることが示せました。
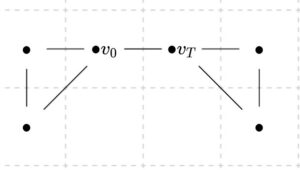
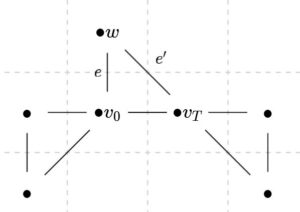
逆に、\(G\)を連結で、奇数次数の頂点を2つだけ持つグラフとしましょう。それらを\(v_0,v_T\)と表します。さきほど同様に、\((v_0,e,w,e^{\prime},v_T)\)が経路となるような頂点\(w\)、辺\(e\)を加えたグラフ\(G_1\)を考えましょう。\(G_1\)においては、2頂点には次数が1加わり、\(v_0,v_T\)の次数が偶数となるので、さきほど示したことにより\(G_1\)はオイラーグラフです。
オイラー経路を\(P=(w_0,f_1,\dots,f_U,w_0)\)と表しましょう。これは\((v_0,\{v_0,v_T\},v_T)\)、\((v_T,e,w,e^{\prime} ,v_0)\)という経路(順番は問わない)を含みます。したがって、経路の順序を並べ替えることで、2つの部分経路を含むオイラー経路\(Q=(v_0,\dots,v_0)\)が作れます。ここで、\(Q\)から\((v_T,e,w,e^{\prime} ,v_0)\)を除いて、順序を入れ替えれば、\(G\)における半オイラー経路が構成できました。
今回示した性質を用いれば、ケーニヒスベルクの橋の問題は解決できます。
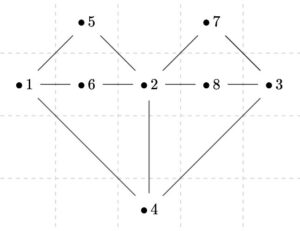
このグラフにおいて、奇数次数の頂点が\(1,2,3,4\)の\(4\)つなので、オイラーグラフでも半オイラーグラフでもありません。すなわち、一筆書きできないことがわかりました。
以上、一筆書きができる条件、オイラーグラフについて紹介してきました。
見分け方のポイントは、奇数次数の頂点の個数です。
- 奇数次数の頂点がなければ、始点と終点が一致する一筆書きができます。
- 奇数次数の頂点が2つならば、始点と終点が異なるような一筆書きができます。
- 奇数次数の頂点が4つ以上ならば、一筆書きはできません。
今回の条件は、あくまで一筆書きの可能性に関するもので、可能なときどのように経路を見つければ良いか(アルゴリズム)については不十分です。おおざっぱには、適当な点から出発して、元に戻る経路を残したまま経路を延長していけば良いです。
そもそもグラフの次数という考え方がなければ、一筆書きができる・できないを見分けるのは難しいでしょう。ぜひいろいろなグラフを考えて、次数を利用して一筆書きできるかどうか考えてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガー・フェアラーク東京 (2002-12T)
¥1,773 (中古品)
丸善出版 (2012-07-17T00:00:01Z)
¥11,800 (中古品)
Graph Theory (Graduate Texts in Mathematics)
Springer (2018-06-05T00:00:01Z)
¥6,933