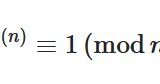オイラーのファイ関数の性質、計算方法

どうも、木村（@kimu3_slime）です。

今回は、オイラーのファイ\(\phi\)関数の性質、計算方法を、具体例を通じて紹介します。

オイラーのファイ関数とは
こちらもおすすめ

オイラーのファイ関数とは

オイラーのファイ関数\(\phi\)は、正の整数\(n\)に対し、\(n\)と互いに素な\(n\)以下の正の整数の個数を返す関数です。

これは数論におけるオイラーの定理「\(a,n\)が互いに素ならば、\(a^{\phi(n)} \equiv 1 \,(\mathrm{mod}\, n)\)」に登場します。\(\phi\)関数のように、正の整数を変数とする関数は、一般に数論的関数と呼ばれています。

今回は、このオイラーの\(\phi\)関数の性質を調べてみましょう。

まずは具体値を求めてみます。互いに素な整数をカウントしていけば良いです。\(1\)は常にカウントされ、\(n\)は常にカウントされません。

\[ \begin{aligned}\phi(1)=1,\phi(2)=1,\phi(3)=2,\phi(4)=2,\phi(5)=4\end{aligned} \]

\[ \begin{aligned}\phi(6)=2,\phi(7)=6,\phi(8)=4,\phi(9)=6,\phi(10)=4\end{aligned} \]

全体的には増加傾向にあるものの、単調に増加しているわけではありませんね。

素数のときの計算

簡単に計算できるのは、\(n\)が素数のときです。素数\(p\)と互いに素なのは、\(1,2,\dots,p-1\)の\(p-1\)なので、\(\phi(p)=p-1\)となります。（逆に、\(\phi(n)=n-1\)ならば\(n\)は素数です。）

さて、約数関数\(\sigma ,\tau\)では、\(n\)が素数のケースを最初に考え、その後\(n\)を素因数分解して計算する方法を導きました。オイラー関数も、同様の計算方法が取れないのでしょうか？　結論から言えば、できます。やってみましょう。

素数べきの計算

まず、\(n\)が素数のべきであるケースを考えてみます。

\(p^2\)と互いに素である数を数えてみましょう。互いに素でない数は、\(p\)で割り切れる数＝\(p\)の倍数のみです。\(p=2\)ならば\(2,4\)で、\(p=3\)ならば\(3,6,9\)が互いに素でない数です。一般には、\(p,2p,3p,\dots,pp\)の\(p\)個が互いに素ではありません。したがって、\(\phi(p^2)=p^2-p\)です。

一般のべき\(p^k\)でも同様に議論できます。互いに素でない数は、\(p,2p,\dots,p^{k-1}p\)の\(p^{k-1}\)個です。したがって、\(\phi(p^k)=p^k-p^{k-1}=p^k(1-\frac{1}{p})\)となります。

素数の積の計算

続いて、\(n\)が異なる素数の積であるケースを考えましょう。

\(n=p_1 p_2\)と互いに素である数を数えるため、\(p_1 p_2\)と互いに素でない数を数えます。\(p_1=2,p_2=3\)のとき、\(2,3,2\cdot2,3\cdot2 \)が互いに素ではありません。互いに素なのは、\(6-3-2+1=2\)個ですね。\(p_1=3,p_2=5\)のとき、\(3,2\cdot3,3\cdot 3,4\cdot3,5\cdot3,5,2\cdot5\)が互いに素ではありません。互いに素なのは、\(15-5-3+1=8\)個です。

一般には、互いに素でないのは\(p_1,2p_2,\dots,p_2p_1,p_2,2p_2,\dots,p_1p_2\)の\(p_2+p_1-1\)個です（\(p_1p_2=p_2p_1\)が重複しているので引く）。よって、\(\phi(p_1p_2)=p_1p_2-(p_2+p_1-1)=(p_1-1)(p_2-1)=\phi(p_1)\phi(p_2)\)が導けました。

一般の場合の計算

さらには、\(\phi\)が乗法的関数であること（\(m,n\)が互いに素ならば、\(\phi(mn)=\phi(m)\phi(n)\)）が示せて、そこから一般の計算式が示せます。

\(n=p_1^{k_1}p_2^{k_2}\cdots p_r^{k_r}\)と素因数分解されたとする。このとき、次の等式が成り立つ。

\[ \begin{aligned} \phi(n)&=(p_1^{k_1}-p_1^{k_1-1})\cdots (p_r^{k_r}-p_r^{k_r-1}) \\ &= n(1-\frac{1}{p_1})\cdots(1-\frac{1}{p_r})\end{aligned} \]

\(\phi\)が乗法的関数であることを認めて、これを確かめてみましょう。\(r\)に関する数学的帰納法で示します。

\(r=1\)のとき、\(\phi(p^k)=p^k-p^{k-1}=p^k(1-\frac{1}{p})\)は既に示しました。

\(r=\ell\)のとき正しいと仮定します。\(p_1^{k_1}p_2^{k_2}\cdots p_\ell^{k_\ell},p_{\ell+1}^{k_{\ell+1}}\)は互いに素なので、乗法的関数の性質が使えます。

\[ \begin{aligned} \phi(p_1^{k_1}p_2^{k_2}\cdots p_\ell^{k_\ell}\cdot p_{\ell+1}^{k_{\ell+1}}) &= \phi(p_1^{k_1}p_2^{k_2}\cdots p_\ell^{k_\ell}) \cdot\phi( p_{\ell+1}^{k_{\ell+1}})\\&= (p_1^{k_1}-p_1^{k_1-1})\cdots (p_r^{k_\ell}-p_r^{k_\ell-1})\cdot(p_r^{k_{\ell+1}}-p_r^{k_{\ell+1}-1}) \end{aligned} \]

となり、確かに成り立つことが示せました。

これらの性質・公式を用いれば、いろいろな\(n\)に対するファイ関数の値が計算しやすいです。

例えば、\(\phi(27)=\phi(3^3)=3^3(1-\frac{1}{3})=18\)と計算できます。

約数との関係

最後に、\(\phi\)関数と約数の関係を紹介しましょう。

\[ \begin{aligned}n=\sum_{d \mid n} \phi(d)\end{aligned} \]

ここで\(\sum_{d \mid n}\)は、\(n\)の正の約数\(d\)すべてに関する和です。

\(n=6\)のとき、正の約数は\(1,2,3,6\)です。そして\(\phi(1)+\phi(2)+\phi(3)+\phi(6)=1+1+2+2=6\)で確かに成り立っています。

\(n\)が素数のとき、約数は\(1,n\)です。したがって、\(\phi(1)+\phi(n)=1+(n-1)=n\)は確かに成り立ちます。

\(n=p^k\)のとき、約数は\(1,p,p^2,\dots,p^k\)です。このとき、\[ \begin{aligned} &\phi(1)+\phi(p)+\cdots+\phi(p^k)\\ &=1+(p-1)+(p^2-p)+\cdots+(p^k-p^{k-1})\\&= p^k \ \end{aligned} \]

とキャンセルして成り立つことがわかります。

\(n=p_1p_2\)のとき、約数は\(1,p_1,p_2,p_1p_2\)です。

\[ \begin{aligned} &\phi(1)+\phi(p_1)+\phi(p_2)+\phi(p_1p_2)\\ &=1+(p_1-1)+(p_2-1)+(p_1-1)(p_2-1)\\&= p_1p_2 \ \end{aligned} \]

と成り立ちます。

一般の場合\(n=p_1^{k_1}p_2^{k_2}\cdots p_r^{k_r}\)は、\(F(n)=\sum_{d \mid n} \phi(d)\)と置くと、\(F\)が乗法的であることが示せます。それを用いれば、

\[ \begin{aligned} F(p_1^{k_1}p_2^{k_2}\cdots p_r^{k_r})&=F(p_1^{k_1})F(p_2^{k_2})\cdots F(p_r^{k_r})\\&= p_1^{k_1}p_2^{k_2}\cdots p_r^{k_r}\end{aligned} \]

と示せるわけです。

以上、オイラーのファイ関数の性質、計算方法を紹介してきました。

整数に関するオイラーの定理は整数論でよく使われるもので、それに合わせて\(\phi\)関数の性質や計算方法を知っておくと役立ちます。例えば、整数の位数や原始根と呼ばれる概念に登場します。（別記事で紹介予定）

定義としては互いに素な数の個数を数えるというものですが、素因数分解できれば簡単に計算できる、というのは便利ですね。

木村すらいむ（@kimu3_slime）でした。ではでは。