どうも、木村(@kimu3_slime)です。
今回は、階乗関数のスターリングの近似を紹介し、その簡単な形を高校レベルの知識で証明しようと思います。
スターリングの近似とは
確率や組み合わせなどの分野で登場する階乗関数\(n!:=1\cdot 2\cdot\cdots \cdot (n-1)\cdot n\)は、\(n\)が大きくなるにつれ爆発的な勢いで増加します。多項式関数や指数関数\(n^k,e^n\)よりも増加が早いです。
\(n!\)は一体どのくらいの量になるのか、既知の関数で近似できないでしょうか。そのひとつが、スターリングの近似(Stirling’s approximation)と呼ばれる近似です。スターリングの公式(Stirling’s formula)とも。
\[ \begin{aligned}n^n e^{-n+1} \leq n! \leq (n+1)^{n+1}e^{-n}\end{aligned} \]
\[ \begin{aligned}n \log n -n +1 \leq \log n! \leq (n+1) \log (n+1)-n\end{aligned} \]
もう少し精度の良い形がありますが、今回はこれを証明しましょう。
スターリングの近似の証明
\(n!\)は積で表された大きな量ですが、対数\(\log\)を取ることである種の和として捉え直すことができます。(\(\log\)は自然対数、底をオイラー数\(e\)とする対数とします)
\[ \begin{aligned}\log n! = \log 1 +\log 2 + \cdots + \log n\end{aligned} \]
となります。この和を、幅\(1\)で高さが\(\log k\) の長方形の面積を足し直したものと見れば、\(\log x\)のグラフがなす面積(積分)\(\int_1 ^n \log x dx\)と比較できます。
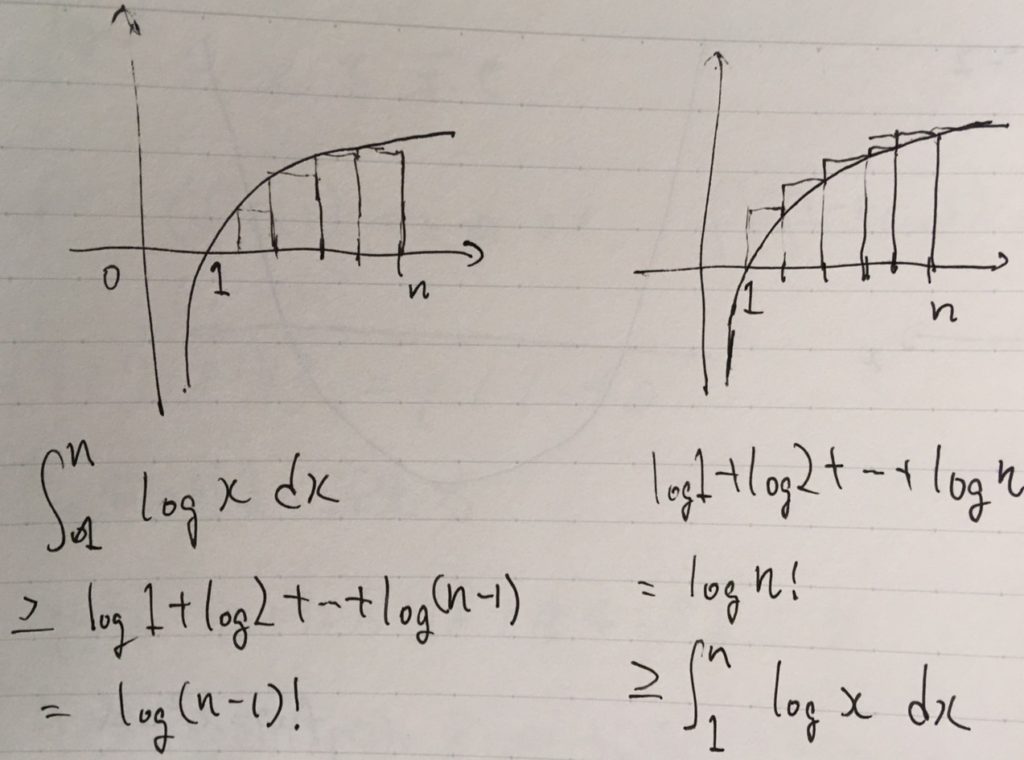
区間\([1,n]\)を、幅1で分割した小区間を考えましょう。
上限和は積分より常に大きく、下限和は積分より常に小さいので、
\[ \begin{aligned}\int_1 ^n \log x dx \leq \log 1 +\log 2 + \cdots + \log n = \log n! \end{aligned} \]
\[ \begin{aligned}\log (n-1)!=\log 1+ \log 2+ \cdots + \log(n-1) \leq \int_1 ^n \log x dx\end{aligned} \]
が成立します。これは積分の定義による性質です。
そして、その積分は部分積分によって計算できます。\((\log x)^{\prime}=\frac{1}{x}\)に注意して、
\[ \begin{aligned} \int_1 ^n \log x dx &= [x\log x]_1 ^n – \int_1 ^n x\frac{1}{x} dx \\ &= n\log n – n+1 \end{aligned} \]
が成立します。よってさきほどの不等式は、
\[ \begin{aligned}\log (n-1)! \leq n\log n – n+1 \leq \log n!\end{aligned} \]
となります。\(n\)は任意だったので、左側の不等式において\(n\)を\(n+1\)に置き換えることで
\[ \begin{aligned}n \log n -n +1 \leq \log n! \leq (n+1) \log (n+1)-n\end{aligned} \]
という形に直せます。指数関数\(e^x\)の単調増加性より、
\[ \begin{aligned}e^{n \log n -n +1} \leq e^{\log n!} \leq e^{(n+1) \log (n+1)-n}\end{aligned} \]
となりますが、対数関数は指数関数の逆関数\(e^{\log x}=x\)であることによって、
\[ \begin{aligned}n^n e^{-n+1} \leq n! \leq (n+1)^{n+1}e^{-n}\end{aligned} \]
と簡易版のスターリングの公式が得られました。
精度の良いスターリングの近似
証明が少し大変になりますが、次の精度が良いスターリングの近似が一般的には利用されます。
\(n! \simeq \sqrt{2\pi} n^{n+\frac{1}{2}} e^{-n}\quad(n\to \infty)\)
この近似\(\simeq \)は、\(\lim _{n\to \infty }\frac{\sqrt{2\pi} n^{n+\frac{1}{2}} e^{-n}}{n!}=1\)を意味する。
詳しくは杉浦「解析入門 Ⅰ」pp.339-340を参照してください。
最初に示した簡易版の近似では、
\[ \begin{aligned}1 \leq \frac{n!}{n^n e^{-n+1}} \leq \frac{(n+1)^{n+1}}{e n^{n}}\end{aligned} \]
であり、上側の評価が\(n\to \infty\)で離れていってしまいます。\(n!\)は\(n^n e^{-n}\)では漸近的に近似することはできないわけです。漸近公式を得るには\(n^{n+\frac{1}{2}} e^{-n}\) が適切で、\(n^{\frac{1}{2}}\)分の差があることに注意しましょう。
プログラミング言語Juliaで計算して、\(n!\)とスターリングの近似の簡易版、良精度版を比較してみました(ウェブ上で見れる実行結果)。
縦軸を\(\log_{10}\)スケール、すなわち桁数とすると、どちらもかなり良い近似ができているのがわかります。
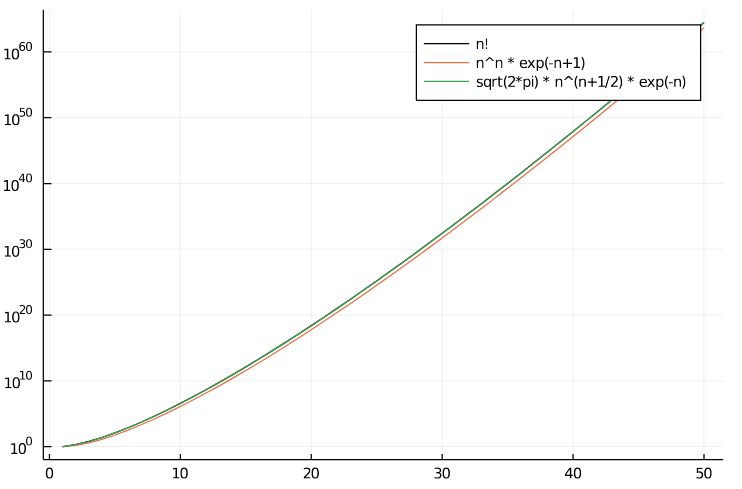
\(n!\)と近似式の比を取ると、簡易版と良精度では差があることがわかります。
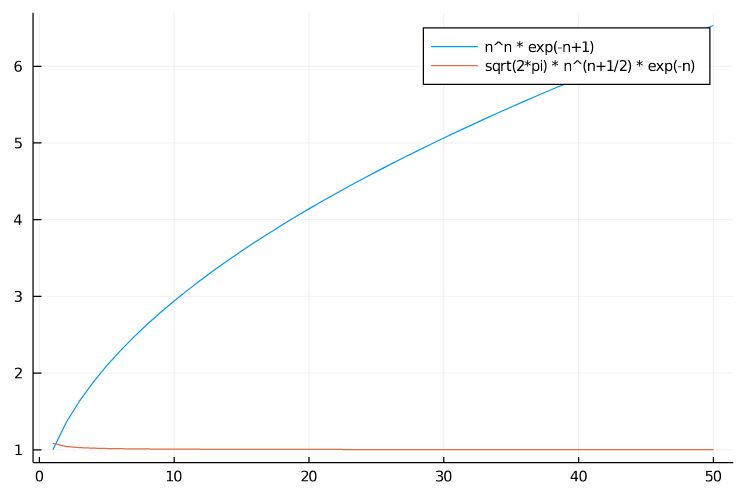
簡易版では\(6\)倍以上の差がついて広がっていきますが、良精度版は比を1に保っていますね。
今回は、スターリングの近似式の簡易版とその証明を紹介し、近似の精度をJuliaで可視化しました。
スターリングの近似は、統計学・確率論の基礎的な定理である中心極限定理の証明にも応用されます(近似によらない別証明もありますが)。
また、階乗関数\(n!\)はガンマ関数\(\Gamma(z)=\int_0^\infty t^{z-1}e^{-t}dt\)と呼ばれる積分で定義された関数に一般化されます。変数が自然数のときには階乗に一致しますが、それ以外の実数や複素数でも値を持っています。ガンマ関数は、初等関数の加減乗除や合成で表せないが有名な関数で、実解析、複素解析の題材として興味深いものです。
\(n!\)は一見すると飛び飛びの値を取る関数ですが、連続な値を持ったグラフの面積\(\int \log x dx\)と比較することができます。何かしら連続的な値を取る関数と関係があるのではないか(ガンマ関数)、そんなことを感じ取ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080