線形方程式の解き方：ガウスの消去法と基本変形・ランク、LU分解

どうも、木村（@kimu3_slime）です。

今回は、線形方程式を解くための方法：ガウスの消去法、その手順を行列によって示す基本変形・ランク、LU分解を紹介します。

ガウスの消去法
行列の基本変形
行列の階段形とランク
LU分解
こちらもおすすめ

ガウスの消去法

連立一次方程式

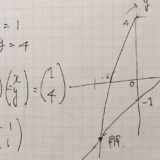
\( \left\{ \begin{array} {l} x-y=1\\ -2x+y=4 \end{array} \right.\ \)

は、\(Ax=b\)という形の線形方程式として表せるのでした。

\( \begin{pmatrix} 1& -1\\ -2 & 1 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ 4 \end{pmatrix}\)

この式を変形していくために、拡大係数行列というものを考えましょう。それは、係数行列\(A\)の最後の列に右辺の\(b\)を付け加えた行列\( \begin{pmatrix} A & b\end{pmatrix} \)です。

\( \begin{pmatrix} 1& -1 & 1\\ -2 & 1 & 4\end{pmatrix} \)

元の方程式で第1式の2倍を第2式に加える操作は、次のような行列の変形として表せます。

\( \begin{pmatrix} 1& -1 & 1\\ -2 & 1 & 4\end{pmatrix} \to \begin{pmatrix} 1& -1 & 1\\ 0 & -1 & 6\end{pmatrix}\)

これはつまり、\(-y=6\)、\(x-y=1\)という式です。求まった\(y=-6\)を代入すれば、\(x=-5\)が求まりますね。

まず、行列の対角成分より左下の成分がすべてゼロになるように、前側の変数を消去していく（前進消去 forward elimination）。その後、後ろ側の変数の値から順に解を求めていく（後退代入 back substitution）。この解き方を、ガウスの消去法（Gaussian elimination）、掃き出し法と呼びます。

3変数の問題でやってみましょう。

\( \begin{pmatrix} 1& 2& 1\\ 2 & 1 &3 \\ 1& 3& 2\end{pmatrix} \begin{pmatrix} x_1\\x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 3\\ 1 \\ 2 \end{pmatrix}\)

この拡大係数行列

\( \begin{pmatrix} 1& 2& 1 & 3\\ 2 & 1 &3 & 1\\ 1& 3& 2 &2\end{pmatrix} \)

を変形していきます。第1行の-2倍を第2行に、-1倍を第3行に加えることで、

\( \begin{pmatrix} 1& 2& 1 & 3\\ 2 & 1 &3 & 1\\ 1& 3& 2 &2\end{pmatrix} \to \begin{pmatrix} 1& 2& 1 & 3\\ 0 & -3 &1 & -5\\ 0& 1& 1 & -1 \end{pmatrix}\)

と\(x_1\)成分が消去できます。第2行を\(-\frac{1}{3}\)倍して、

\(\begin{pmatrix} 1& 2& 1 & 3\\ 0 & -3 &1 & -5\\ 0& 1& 1 & -1 \end{pmatrix} \to \begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 1& 1 & -1 \end{pmatrix}\)

で、さらに第2行の-1倍を第3行に加えれば

\(\begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 1& 1 & -1 \end{pmatrix} \to \begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 0& \frac{4}{3} & -\frac{8}{3} \end{pmatrix}\)

と、単純な形に変形できました（前進消去）。

残るは、\(\frac{4}{3}x_3 =-\frac{8}{3}\)、\(x_2-\frac{1}{3} x_3 =\frac{5}{3}\)、\(x_1+ 2x_2+x_3 =3\)を順に代入して解が得られます（後退代入）。すなわち、\((x_1,x_2,x_3)=(3,1,-2)\)です。（元の方程式に代入して、正しいことをチェックしてみてください）

行列の基本変形

線形方程式を解くための変形、ガウスの消去法で許される変形は、次の4種類です。

ある行を定数倍する（0倍を除く）
ある行の定数倍を別の行に加える
ある行と別の行を入れ替える
ある列と別の列を入れ替える

4.は、変数の取替えで、\(b\)を表す最後列を除いたものです。

実は、これらの操作はすべて行列（の積・作用）として表せます。

行列の積について：行列の積の定義はなぜあの形？変換の合成として見る

さきほどの変形を、行列を使って表現してみましょう。

第1行の-2倍を第2行に、-1倍を第3行に加える操作は、

\( \begin{pmatrix} 1& 0&0 \\ -2 & 1 &0 \\ -1& 0& 1\end{pmatrix} \begin{pmatrix} 1& 2& 1 & 3\\ 2 & 1 &3 & 1\\ 1& 3& 2 &2\end{pmatrix} \ =\begin{pmatrix} 1& 2& 1 & 3\\ 0 & -3 &1 & -5\\ 0& 1& 1 & -1 \end{pmatrix}\)

と表せます。第\(i\)行を第\(j\)行に\(c\)倍して加える操作を表す行列は、単位行列の成分を、\((j,i)\)成分だけ\(c\)に変えた行列です。

第2行を\(-\frac{1}{3}\)倍する操作は、

\(\begin{pmatrix} 1& 0& 0\\ 0 & -\frac{1}{3} &0\\ 0& 0& 1 \end{pmatrix}\begin{pmatrix} 1& 2& 1 & 3\\ 0 & -3 &1 & -5\\ 0& 1& 1 & -1 \end{pmatrix} = \begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 1& 1 & -1 \end{pmatrix}\)

です。第\(i\)行を\(c\)倍する操作は、単位行列のうち\((i,i)\)成分だけ\(c\)に変えたものです。

第2行の-1倍を第3行に加える操作は、さきほど同様、

\(\begin{pmatrix} 1& 0&0 \\ 0 & 1 &0 \\ 0& -1& 1\end{pmatrix} \begin{pmatrix} 1& 2& 1 & 3\\ 0 & -3 &1 & -5\\ 0& 1& 1 & -1 \end{pmatrix} = \begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 0& \frac{4}{3} & -\frac{8}{3} \end{pmatrix}\)

です。今回は必要ありませんでしたが、第1行と第3行を入れ替える操作は

\(\begin{pmatrix} 0& 0&1 \\ 0 & 1 &0 \\ 1& 0& 0\end{pmatrix} \begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 0& \frac{4}{3} & -\frac{8}{3} \end{pmatrix} = \begin{pmatrix} 0& 0& \frac{4}{3} & -\frac{8}{3} \\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 1& 2& 1 & 3 \end{pmatrix}\)

と表せます。\(i,j\)行を入れ替えたいなら、単位行列を\(i,j\)行だけ入れ替えた行列を使えば良いです（置換行列）。例えば拡大係数行列の\(1,1\)成分が0の問題を考えるときは、第1列が0でない行と第1行を入れ替える必要がありますね。

行列の階段形とランク

ある行を定数倍する（0倍を除く）
ある行の定数倍を別の行に加える
ある行と別の行を入れ替える
ある列を定数倍する（0倍を除く）
ある列の定数倍を別の列に加える
ある列と別の列を入れ替える

こうした行列の変形を、基本変形（elementary operation）と呼びます。特に前半3つは、左基本変形、行基本変形。後半は3つは右基本変形、列基本変形とも。

基本変形を表す行列は、基本行列（elementary matrix）と呼ばれます。単位行列をちょっといじれば、基本行列は求められます。

拡大係数行列に限らず、一般の行列\(A\)は、基本変形によって次の階段形（echelon form）、標準形に変形できます。

\(A \to \begin{pmatrix} I_r & O\\ O &O\end{pmatrix} \)

\(I_r\)はサイズ\(r\)の単位行列、\(O\)は適当なサイズのゼロ行列です。

このとき、階段形に含まれている単位行列のサイズは行列\(A\)のみによって決まり、基本変形の仕方によりません。このサイズ\(r\)を行列のランク・階数（rank）と呼び、\(\mathrm{rank} A =r\)と書きます。

証明について詳しくは、「線型代数入門」のp.50 定理[4.2]を参照してください。

今回の拡大係数行列のランクは

\( \mathrm{rank} \begin{pmatrix} 1& 2& 1 & 3\\ 2 & 1 &3 & 1\\ 1& 3& 2 &2\end{pmatrix} = \mathrm{rank}\begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 0& 1 & -2 \end{pmatrix} =3\)

です。一方で、もともとの係数行列のランクも

\( \mathrm{rank} \begin{pmatrix} 1& 2& 1 \\ 2 & 1 &3 \\ 1& 3& 2 \end{pmatrix} = \mathrm{rank}\begin{pmatrix} 1& 2& 1 \\ 0 & 1 &-\frac{1}{3}\\ 0& 0& 1 \end{pmatrix} =3\)

です。これらのランクは等しいですね。

係数行列と拡大係数行列のランクが等しいことは、線形方程式\(Ax=b\)が解を持つための必要十分条件であることが知られています。

参考：「線型代数入門」のp.59 系[5.3]

もし拡大係数行列が

\(\begin{pmatrix} 1& 2& 1 & 3\\ 0 & 1 &-\frac{1}{3}& \frac{5}{3}\\ 0& 0& 0 & -2 \end{pmatrix} \)

となるような問題を考えれば、確かに第3行から\(0=-2\)と矛盾が導かれるので解は存在せず、ランクが落ちていることがわかりますね。行列のランクは、線形方程式のうち有効に機能している式の本数と言えるでしょう。

LU分解

今回行ったガウスの消去法は、行列を2つの三角形の形の正方行列に分解したものと見ることもできます。

\( A = \begin{pmatrix} 1& 2& 1 \\ 2 & 1 &3 \\ 1& 3& 2 \end{pmatrix}\)

\(U = \begin{pmatrix} 1& 2& 1 \\ 0 & 1 &-\frac{1}{3}\\ 0& 0& \frac{4}{3} \end{pmatrix}\)

\(L ^{-1}= \begin{pmatrix} 1& 0&0 \\ 0 & 1 &0 \\ 0& -1& 1\end{pmatrix} \begin{pmatrix} 1& 0& 0\\ 0 & -\frac{1}{3} &0\\ 0& 0& 1 \end{pmatrix} \begin{pmatrix} 1& 0&0 \\ -2 & 1 &0 \\ -1& 0& 1\end{pmatrix} \)

と置きます。\(U\)は基本変形を施していった後の階段形で、\(L^{-1}\)は行った3回の基本変形をあわせたものです。

\(L L^{-1}=I\)となる行列（逆行列）を求めると、

\(L = \begin{pmatrix} 1& 0&0 \\ 2 & 1 &0 \\ 1& 0& 1\end{pmatrix} \begin{pmatrix} 1& 0& 0\\ 0 & -3 &0\\ 0& 0& 1 \end{pmatrix} \begin{pmatrix} 1& 0&0 \\ 0 & 1 &0 \\ 0& 1& 1\end{pmatrix} \\ = \begin{pmatrix} 1& 0&0 \\ 2 & -3 &0 \\ 1& 1& 1\end{pmatrix} \)

つまり、\(L^{-1} A =U\)、すなわち\(A=LU\)という形になります。

ここで\(U\)は対角成分より下側が0の行列（上三角行列 upper triangular matrix）で、\(L\)は対角成分より上側が0の行列（下三角行列 lower triangular matrix）となっています。このような三角行列への分解\(A=LU\)は、LU分解（LU decomposition）と呼ばれるものです。

\(L\)は前進消去に、\(U\)は後退代入に対応していて、ガウスの消去法が行っていたことは、このような行列の要素分解・単純化と言えます。

コンピュータで線形方程式\(Ax=b\)を解くときは、ガウスの消去法を行うより、LU分解してから計算する方が、行列のサイズ\(n\)が大きくなるときの計算量が少ないことが知られています。\(Ly=b, Ux=y\)と2つに分解すると、それぞれが三角行列なので計算が簡単になっています（前進代入と後退代入になっている）。

LU分解は、すべての正方行列で可能なわけではありません。逆行列を持つ行列では、その行列の左上\(k\times k\)の部分行列\(A_k\)がすべて逆行列を持つことが、LU分解できるための必要十分条件です。逆行列を持たない一般のケースでも、LUに似た分解ができることが知られているようです。

参考：Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6. See Section 3.5. N − 1、 Okunev, Pavel; Johnson, Charles R. (1997), Necessary And Sufficient Conditions For Existence of the LU Factorization of an Arbitrary Matrix

以上、ガウスの消去法、行列の基本変形とランク、LU分解について紹介してきました。

線形代数を初めて学ぶ人は、まずガウスの消去法だけでも身につけてもらえたらなと思います。消去法が身についていないと、行列のランクや逆行列の計算に戸惑うかもしれません。行列をシンプルに変形するアイデアは、とても便利です。

木村すらいむ（@kimu3_slime）でした。ではでは。