1次方程式を行列で解くメリット・方法・条件について、幾何学的に見る

どうも、木村（@kimu3_slime）です。

今回は、連立1次方程式（線形方程式）を行列によって解く意味・方法、その幾何学的意味、解ける条件を、2次元のケースで紹介したいと思います。

1次方程式が解けるメリット
線形方程式を行列で表し、幾何学的に見る
線形方程式が解ける条件
こちらもおすすめ

1次方程式が解けるメリット

線形代数学では、まず行列の計算について学びます。その応用例としては、連立一次方程式を解くことが挙げられるでしょう。行列は1次方程式を解くのに役立つわけです。

1次方程式が解けて、何が嬉しいのでしょうか。例えば二元連立1次方程式なんて、つるかめ算として小中学生で学ぶものです。行列で表して難しく見せるだけなら、意味がないような気がします。

線形代数学の理論では、大きなサイズの1次方程式を解くことをも想定しています。二元連立、三元連立どころか、100や1000個連立させるのです。そのために、行列のサイズを一般の\(n\)にして考えた理論を作ります。

1次方程式というとなんだか単純そうかもしれませんが、それは線形方程式（linear equation）とも呼ばれます。ここからは、1次方程式ではなく、線形方程式という呼び方を使っていきましょう。

数学や科学全般において、捉えたい問題を数式によって表すわけですが（モデル化）、大雑把にそのモデルは、線形のモデルと非線形のモデルに分かれます。

線形のモデルは、線形代数学によって効率的に解く方法が知られているものが多く、解きやすいです。非線形の問題では、そのような方法が少なく、個別の工夫が必要になります。そのため、非線形モデルを線形モデルに近似して解くことがあります。つまり、非線形モデルを扱う上でも、最初に線形モデルの解き方を知っておく必要があるわけです。

参考：数学・科学における「線形・非線形」の違いを詳しく解説

例えば物理的なモデルは微分方程式によって表されることが多いですが、それは長さや時間など連続的な値を持つものです。数学的・理論的に解けるケースでは連続値は都合が良いのですが、きれいに解けないケースでは数値解を求めるために、離散的な値で近似をします。コンピュータにおける数値シミュレーションでは、微分方程式という連続的な方程式を、線形方程式という離散的な方程式によって近似するのです。例えば1つの区間を\(n\)個に割るわけですが、より良い近似にしようと思えば\(n\)を大きくする必要があり、大きな\(n\)での行列計算が必要とされるわけです。

参考：線形方程式の解法：直接法

線形方程式を行列で表し、幾何学的に見る

とはいえ、いきなり一般の\(n\)で考えると難しいので、まずは\(n=2\)のときで話をしていきます。

連立一次方程式は、行列とベクトルによって表すことができます。例えば、

\( \left\{ \begin{array} {l} x-y=1\\ -2x+y=4 \end{array} \right.\ \)

は

\( \begin{pmatrix} 1& -1\\ -2 & 1 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ 4 \end{pmatrix}\)

と表せます。2つの式を2次元のベクトルとしてまとめ、その上で、左辺の係数を行列として取り出したわけです。

\(n\)個連立させた1次方程式は、

\( \left\{ \begin{array} {l} a_{11} x_1 +\cdots+ a_{1n}x_n=b_1\\ \vdots \\ a_{k1}x_1 +\cdots+a_{kn} x_n = b_k\\\vdots \\ a_{n1}+\cdots +a_{nn} x_n=b_n \end{array} \right.\ \)

行列を\(n\times n\)のサイズ、\(x=(x_1,\dots,x_n),b=(b_1,\dots,b_n)\)とすれば、線形方程式は\(Ax=b\)と簡単に表せます。\(A\)の\(i\)行\(j\)列の成分は、\(a_{ij}\)です。

さて、上の方程式を幾何学的に見てみましょう。

1つ1つの式（行ベクトル）に注目して、それを\(x,y\)平面に図示します。

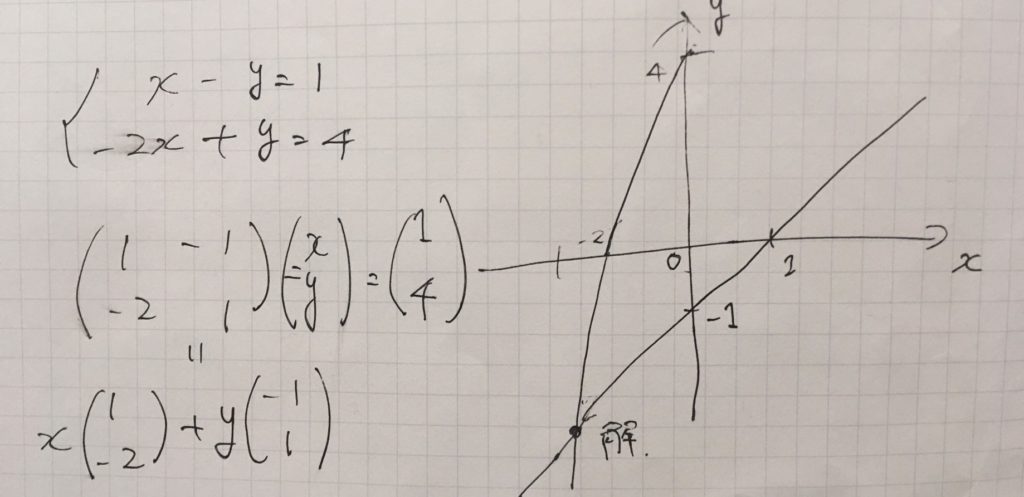
この線形方程式は2つの直線を表し、そしてその交点\((x,y)\)が解というわけです。もし3本の方程式になったとしても、3つの平面が交わる点が解となります。

参考：2変数関数と偏微分：グラフ、接平面を描いてみよう

傾きのある2本の直線の交点を求めるのは、少し面倒です。（この程度の問題なら簡単ですが、変数が増えると大変でしょう）

そこで、元の方程式を代数的に変形して解いてみます。1番目の式を2倍して、2番目の式に加えることで、\(x\)が消去できて、\(y\)のみの式になります。再びこれを図示してみましょう。

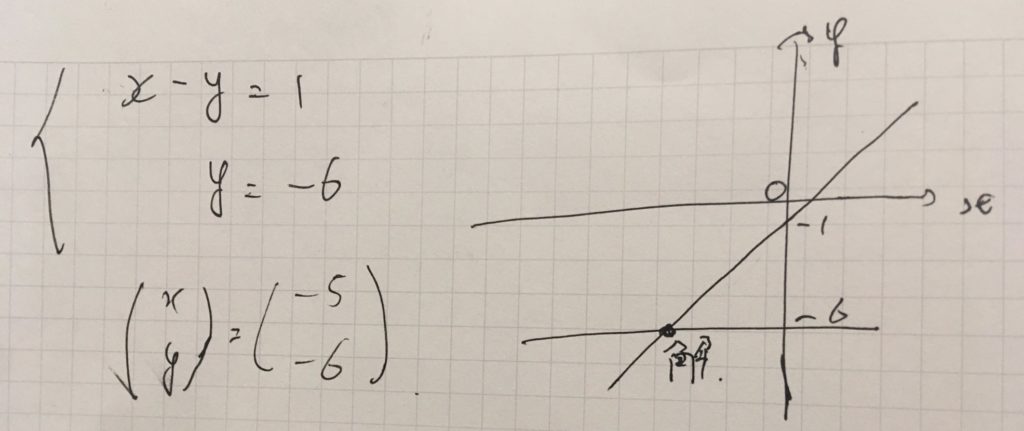
2本の直線の交点が解であるわけですが、一方の直線を条件を満たしたまま変形することで、\(y=-6\)という傾きのない直線にできました。\(y\)が求まれば、\(x\)を求めるのは簡単です。最終形は\(x=-5,y=-6\)という2つの直行する直線の交点として求められました。

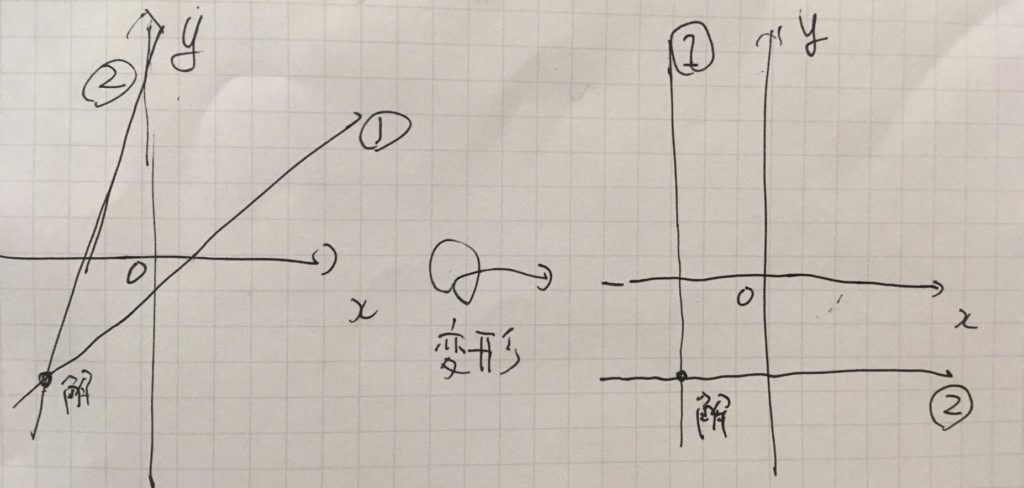
連立方程式を解くことは、幾何学的には、直線や平面（そして超平面）の交点を求めることです。そして方程式を変形して変数を減らす操作は、斜めになった直線や平面（超平面）を、軸に並行で傾きのないものに直すことに対応しています。

このように、方程式をシンプルに変形する方法、変数を先に消去して後から代入する方法は、一般にガウスの消去法、掃き出し法として知られています。別記事で紹介予定。

線形方程式が解ける条件

中学校で学ぶ連立一次方程式は、解がただ一つに定まり解けるケースを考えることが多いかと思います。しかし、一般にはそれは正しくありません。

例えば、次の方程式を考えましょう。

\( \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ -4 \end{pmatrix}\)

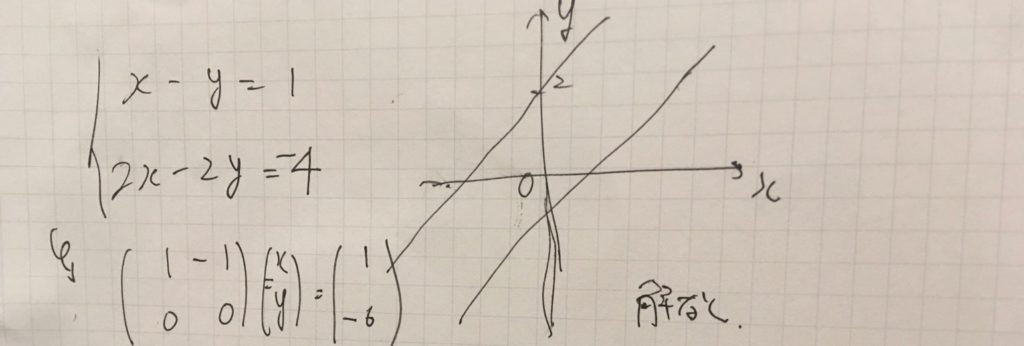
代数的に解こうとすると、\(0=-6\)という式が出て矛盾するので、これを満たす解\(x,y\)は存在しません。

幾何学的に見れば、方程式は2つの平行な直線を表しています。平行な直線同士に交点はないので、解も存在しない、というわけです。

別の例を考えてみます。

\( \begin{pmatrix} 1& -1\\ 0 & 0 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ 0 \end{pmatrix}\)

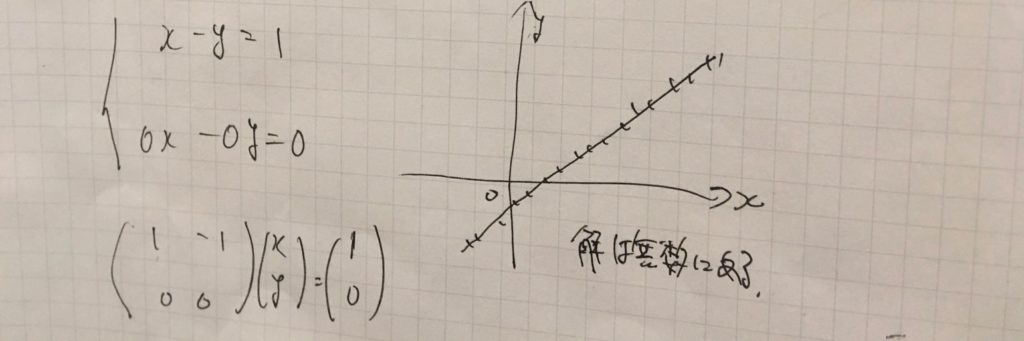
2つ目の式が実質的に何の条件も課していない（退化している）ケースです。

\(x-y=1\)を満たす\(x,y\)、例えば\((2,1),(3,2)\)などはすべて解です。つまり、\(c\)を任意の実数として、\((x,y)=(c,c-1)\)が解となります。

幾何学的に見れば、一方の直線は指定されず、\(x-y=1\)という直線上のすべての点が解です。

3つの方程式は、何が違ったのでしょうか。

\( \begin{pmatrix} 1& -1\\ -2 & 1 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ 4 \end{pmatrix}\)

\( \begin{pmatrix} 1& -1\\ 2 & -2 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ -4 \end{pmatrix}\)

\( \begin{pmatrix} 1& -1\\ 0 & 0 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} 1\\ 0 \end{pmatrix}\)

行列を2つの行ベクトルを並べたものと見ましょう。

2番目の式では、\(-2(1,-1)+(2,-2)=(0,0)\)で、係数が完全に消えてしまいます。一方で、1番目では、2つの行ベクトルをどんな風に定数倍して加えても、消えることはありません。幾何学的に言えば、2番目の式ではベクトルが平行で、1番目では平行ではありません。この違いは、線形従属、線形独立という言葉で説明できます。

参考：実数空間、線形結合、線形部分空間、次元とは何か：2次元を例に

一般に、「ある行列の行ベクトル・列ベクトルのうち、線形独立なものの最大個数」をその行列のランクと呼びます。

線形方程式に解が存在するかどうかを調べるためには、係数行列と、定数項を含む行列（拡大係数行列）のランクを比較します。ランクが等しければ存在し、そうでないなら存在しません。

線形方程式が解ける条件、ランクと線形独立性については別記事で紹介予定です。

以上、線形方程式が解けるメリット、代数的な解き方とその幾何学的な意味、解ける条件について例を交えて紹介しました。

単なる行列操作だけでなく、幾何学的な視点をセットで考えると、線形代数学の視点が身につけやすいと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。