どうも、木村(@kimu3_slime)です。
数学が嫌いだ、または苦手だなと思うことはありますか?
僕自身は大学で数学を学んだのでそうでもないのですが、学校教育を通して嫌いになってもおかしくありません。好き嫌いは強制できることではありませんし、嫌いで良いと思うんです。でも、本人に関係ない環境的なきっかけで、数学から離れてしまう人がいるのは惜しい。
今回は、数学嫌いな人へのアンケート調査をもとにした本「人はなぜ数学が嫌いになるのか」を参考に、数学嫌いのありがちな要因を取り上げ、その原因や対策について考えてみます。
公式を暗記する科目だと思ってしまう
数学につまづく、嫌いになるきっかけのひとつが、公式を暗記させられることです。
2次方程式の解の公式、サイン・コサインの公式とか。あれもこれも覚えさせられ、覚えきれなくなっていく。
\[ \begin{aligned}x= \dfrac{-b \pm \sqrt{b^2 -4ac}}{2a}\end{aligned} \]
この公式で言えば、\(b\)が偶数の時のパターンが書いてあったりします。そんなの個別に覚える必要はないです。約分すればいいだけ。でも、苦手な人は、「教科書にはたくさん書いてあるから、枠で囲ってある公式こと、全部覚えないとダメなの……?」と絶望していくでしょう。
数学は、決して公式に数を当てはめて計算するだけの科目ではありません。論理的に物事を考え、記号を使った式を使って着実に説明する科目です。その論証のいち部分に、計算という手段があるのです。
「人はなぜ数学が嫌いになるのか」において、中学高校の数学教育は、計算偏重であるという指摘がされています。
算数の伝統的なやり方を、中学や高校の数学に当てはめてしまっている面があるでしょう。小学校の計算問題ならば、ドリルで鍛えられる部分はあります。しかし、数学はパズル的に「答え」だけを当てるゲームではありません。
こうした教育になる原因のひとつに、マークシート式の試験(の採点配分の高い大学が多い)ことがあります。
マークシート式の試験では、途中式の計算は求められず、答えの数字(それも桁のわかっている整数)を求められることが多いです。\(\sqrt{}\)□□で2桁だから11、13かな、といった当てずっぽもできてしまいます。
公式を使った計算問題は、できれば面白いかもしれませんが、覚えきれないと苦行です。こんな計算、試験以外の何に使うのだ、いや使わないだろうとなってしまいます。
2020年現在、コンピューターは発展してきており、ミスなく数値計算できることの価値は下がってきています。単純計算は、電卓やコンピューターに任せれば良いのです。ビジネスや研究でもそうしていることが多いでしょう(学校現場でもそうしてほしいです)。
ではなぜ数学を学ぶかといえば、そのコンピュータに適切に計算式や計算手順(アルゴリズム)を与えるためです。最終的な値を求めるだけでなく、問題を設定し、それを解決するための手順(式変形や証明)を得るのが大事です。この能力はマークシート式試験では測りにくいです(改善しようとする試みはあるようですが)。
もし公式の暗記で数学が嫌になったら。まずそれは数学そのもののせいでなく、マークシート式試験が要因です。もしそれがつまらないなと思ったら、その公式の導き方を調べたり、公式同士の関連性を見つけて、できるだけ覚える量を減らしてみましょう。
一度遅れると、取り返すのが難しい
特に数学が嫌いになるのがこれ! 一回内容についていけなくなって、遅れが挽回できずに脱落してしまうやつです。
数学は積み重ねの学問です。例えば文字式の因数分解が苦手な人は、数の素因数分解が苦手だったり、さらにその原因は掛け算割り算の苦手意識だったりします。他の科目ならば、一度ついていけなくなったとしても、この分野ならば最初から理解できるという挽回が起こります。数学の場合、わからなくなった時点まで戻っていかなければ、その先についていくのはほぼ不可能になります。
自分の学年以前の内容がわかっていないのは、恥ずかしいことでは全くありません。むしろ当然です。誰だって気がのらないこと、相性の悪いことはあります。一回言われて全部理解できるなら、学校や教師は必要ありません。
しかしながら、日本の学校教育は一度遅れた生徒・学生へのサポートが薄いです。学年・学期ごとに割り当てられたカリキュラム・教科書を淡々と消化していきます。できる人が飛び級する制度も少ないですし、その逆、ついていけない人への再授業(リメディアル教育)も少ないです。
数学の授業で、わからないことがあったときに、授業中や授業後に質問にいけるでしょうか? 難しいと感じる人は多いのではないでしょうか。日本のクラスは中学校で平均約34人と、欧米の20-25人と比べ多いです。
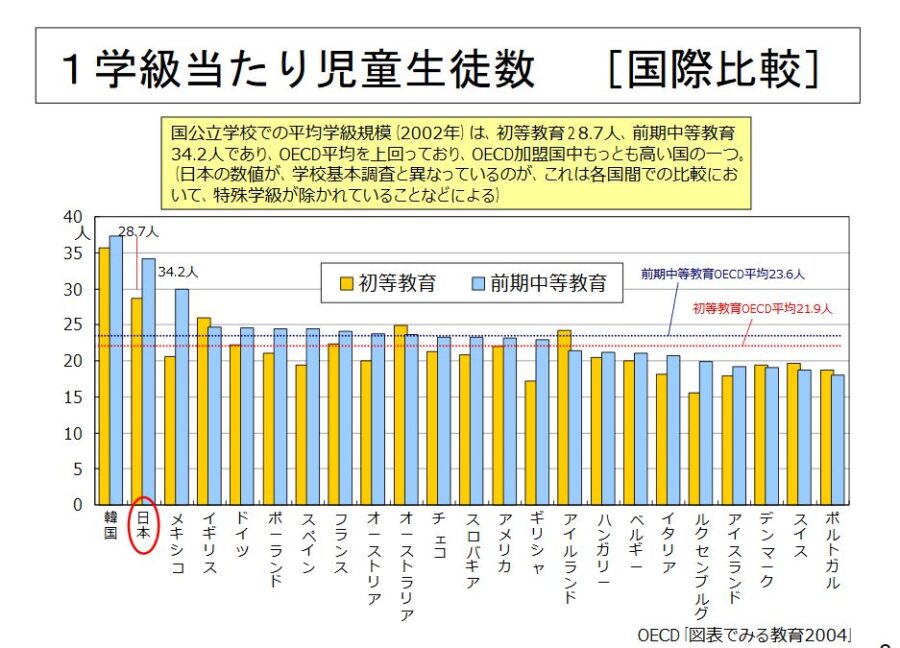
引用:1学級当たり児童生徒数 [国際比較] – 調査研究協力者会議等(初等中等教育)/文部科学省
クラスの人数が30人以上の大人数教育だと、ついていけない生徒に個別のサポートをするのは難しいです。少人数教育、個別授業ならばこれを補うことができます。
現状日本の学校教育で、すぐに大人数教育をなくすようなことにはならないでしょう。結果として、サポートの手厚い私立の学校、または塾に通える人だけが、数学の遅れを取り戻すことができる。そうでない人は、数学は自分のものではないとリタイアしていく。
これに関しては、制度的な限界であり、学校の先生が悪いとは思いません。ついていけない人への復習・独学を支援できるような情報・教材を増やす必要があるでしょう。このサイトでも提供していきたいと思います。
数学は役に立たない・数学はセンス?
数学についていけなくなるとどうなるか。あきらめる、またはできなくていいやと正当化していきます。だって人間だもの。
周囲の人や環境が、それを後押しすることもあるでしょう。
学生のコメント文にも、本節の題(「数学ができない血筋だ、と親に言われた」)のほかに「自分は血筋からしてダメだという先入観を植え付けられた」、「両親が文系だから理数系は向いていない、と諭された」というように、数学の得意・不得意に関して、まるで犬の血統書のようなものをつけてみる見方が定着しているようにさえ感じます。そして、そのような見方から数学に苦手意識を植え付けられた生徒は、数学が不得意になって、数学嫌いになるパターンにはまってしまうのでしょう。
引用:人はなぜ数学が嫌いになるのか pp.48-49
ここで指摘されていますが、日本の教育制度における文理分けの問題は根深いと思っています。文系だから数学は苦手で良い、数学が苦手だから文系に進む、という枠組みにハマって数学への気力が削がれるのはもったいないです。
およそ大学で学問を学びたいならば、いわゆる文理にかかわらず、数学を使います。論理的に考える力はどの学問でも使いますし、現象をモデル化する理論的な分析、アンケート調査による実証的・統計的な分析は、いわゆる文系の学問にも必要です。
文系で数学が苦手な人が多いけど、自分は数学が嫌いじゃないから、定量的なアプローチの調査や研究ができる。それは将来の自分の強み、アドバンテージとなります。
数学は、確実に段階を踏んでいけば、誰でもできるようになります。それが人より遅いか早いかなんて気にしなくても良いです。センスやひらめきが必要、なんてことはありません。スポーツやゲームも、学び始めには難しさがあります。でも、ちょっとずつできることが増えていくときっと楽しくなるでしょう。
数学をやらなくても良いやと思う理由には、数学は(実際的なことの)役に立たないじゃないかという指摘もあるでしょう。自分は数学を使う仕事に就かないから、という視点です。そもそも、勉強は受験や仕事のためだけにするものではないのですが……。
これは中学高校の数学のカリキュラム、教科書にも原因があります。物理や化学、他の教科と連携するエピソードは少ないです。人物や歴史に関する記述や、ビジネス・実社会への応用も語られにくいです。
例えば素因数分解について習うときに、安全な通信をするための暗号に役立っている話とか聞きたかった。イギリスの数学者チューリングの暗号解読を扱った映画「イミテーション・ゲーム」は、数学の専門家が社会に役立つことや、彼自身の個性と葛藤が描かれていておすすめです。
科目としての数学には、「今は何に使うかわからなくても、将来使うから学べ」という教える側の都合に沿った押し付けがましさがあります。学ぶ側の視点が軽視されているのです。
当たりの先生に出会えれば、今の学びと将来や他の分野を交えた話をしてくれるでしょう。しかしそれは稀だと思います。数学の教え方は、現状理不尽な部分がありますが、考えることをあきらめないでください。何の役に立つのかという疑問はまっとうです。それを適切な人に聞いたり、調べたり考えたりすることは、きっと人生を深みのあるものにしてくれると思います。
人と違う意見を述べるのが怖い
最後に紹介するのは、自分の体感としてはありますが、ちょっと根拠のふわっとした話です。
数学を学ぶときには、試行錯誤や間違えることは大事です。にもかかわらず、教育の中で間違えたり、言う通りのやり方でないと恥ずかしいと思わされることがあります。
それゆえ数学好きな人は、事細かに型にはめた解法の矯正や、問題を好き勝手に試行錯誤しながら考えている途中で思考を停止させられることを本質的に嫌います。実は、私が学生のコメント文で一番注目した点はこのことに関することで、せっかく数学好きになる芽が出かかっているときに、その芽を刈るような発言によって数学を嫌う気持ちが決定的になったことを訴えるものが数多くありました。
その代表的なものを挙げると、「小学校で『先生の言う通りでない回答はダメ』と言われた」、「理解して乗り越えようとしているのに経過時間を馬鹿にされた」、「生徒の理解より、教科書そのままを優先された」、「短時間で形式に沿って解くセンター入試のような問題が大嫌い」等々。
引用:人はなぜ数学が嫌いになるのか pp.63-64
例えば小学校の算数教育では、掛け算の順序強制問題や、筆算における定規の使用を強制する問題が話題となっています。数学の魅力のひとつに、正しい論証であれば手順は自由であることが挙げられます。しかし、教師・もといカリキュラムや教育学部の問題があり、生徒を型にはめようとする、平均から外れた人を減らそうとすることがあるようです。
本では、日本人は英語圏でもディベートが苦手である、また論理的思考に基づいて議論する習慣がないと指摘されています。誰がなんと言おうが、人と違った意見でも自由に述べて良い。客観的・論理的なアウトプットをする習慣は、日本の学校教育では現状育まれにくいです(国語の学習指導要領に「論理国語」が追加されることで、少し改善されるかもしれませんが)。
数学を学ぶことは、自分の意見を持ち、人にそれを説明するトレーニングであると思います。論理のトレーニング、論理学の勉強が必要です。これが数学教育、学校教育には欠けています。
例えばこれは文章題の読解力にも影響してきます。すべての\(x\)が満たす式=恒等式と、ある\(x\)が満たす式=方程式の違いを、きちんと意識的に授業で説明されたことはあるでしょうか。論理がわかっていなければ、数学を理解し、それを人に説明する(証明を書く)のは至難の業になります。
数学が学校教育でこれほどの重点が置かれているのは、それを通じて論理的な思考が身につくからだと僕は考えています。論理的な思考は、知的な仕事や民主主義の基礎です。せっかく学校で何か学ぶならば、自らの意見を持ち、それを色々な人にわかるように説明できる力を身につけたいものですね。
参考:論理学の入門ロードマップ:大学数学に必要な論理学とは、論理学の考え方、命題、主張、仮定、結論とは何か?
たとえ数学が嫌いになりそうでも、それには理由があります。苦手であっても良いですが、できれば嫌いにならないで、楽しむ気持ちを見出してもらえればと願います。考えることをあきらめなければ、ちょっとしたことで好きになったり得意になったりすることがあるでしょう。
今回参考にした「人はなぜ数学が嫌いになるのか」は、人文系の大学生に対するアンケートをもとにしていて、他にも多くの理由が分析されています。Kindleの読み放題サービスKindle Unlimitedの対象になっているので、ぜひチェックしてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
人はなぜ数学が嫌いになるのか (PHPサイエンス・ワールド新書)
PHP研究所 (2010-09-17T00:00:00.000Z)
¥750
こちらもおすすめ
「数学は何の役に立つのか」「じゃあ学問は役に立つためにあるのか?」



