どうも、木村(@kimu3_slime)です。
教養数学における微積分学や線形代数学のひとつの目標は、多変数関数の扱い方を理解することだと思います。
今回は、簡単な2変数関数を例に、偏微分を使ってそのグラフを描く方法を考えてみましょう。
前提知識:集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える、実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に
平面(線形関数)のグラフ
例えば、\(f_1(x,y):=2x-3y\)という関数を考えてみましょう。\(f(1,0)=0,f(0,2)=-6\)です。2つの数\((x,y)\)が決まれば、\(2x-3y\)という値が実数として決まります。
このような関数\(f:\mathbb{R}^2\to \mathbb {R}\)は、2変数関数(functions of two variables)と呼ばれます。変数が\(N\)個ならば、\(N\)変数関数です。これらの総称が、多変数関数(functions of several varibales)です。
最も簡単な2変数関数は何でしょうか? 高校までの数学では、二次関数や指数関数を扱う前に、まず一次関数\(f(x)=ax\)を扱います。
多変数の1次関数と呼べるのが、線形関数\(f(x,y)=ax+by\)です。\(f_1(x,y)=2x-3y\)を例に、そのグラフを描いてみましょう。
2変数関数の変数\((x,y)\)を表すためには平面\(\mathbb{R}^2\)が必要で、かつそのグラフを描くためには値を表すための軸\(\mathbb{R}\)が必要です。結果として、2変数で実数の値を持つ関数のグラフを描くには、3次元空間\((x,y,f(x,y))\in \mathbb{R}^3\)を考える必要があります。
\(f_1(x,y)=2x-3y\)のグラフは、どうやって描いたら良いでしょうか? \((x,y)=(0,0),(0,1),(1,0),(0,2),\dots\)とやっていたら、確実ですが、キリがありません。
有効なのが、まず\(x\)または\(y\)、いずれかの値を決めてしまうことです。例えば、\(y=0\)のときを考えれば、\(f_1(x,0)=2x\)で、これは簡単ですね。また、\(x=0\)ならば\(f_1= -3y\)です。
これを図に落とし込むと、次のようになります。
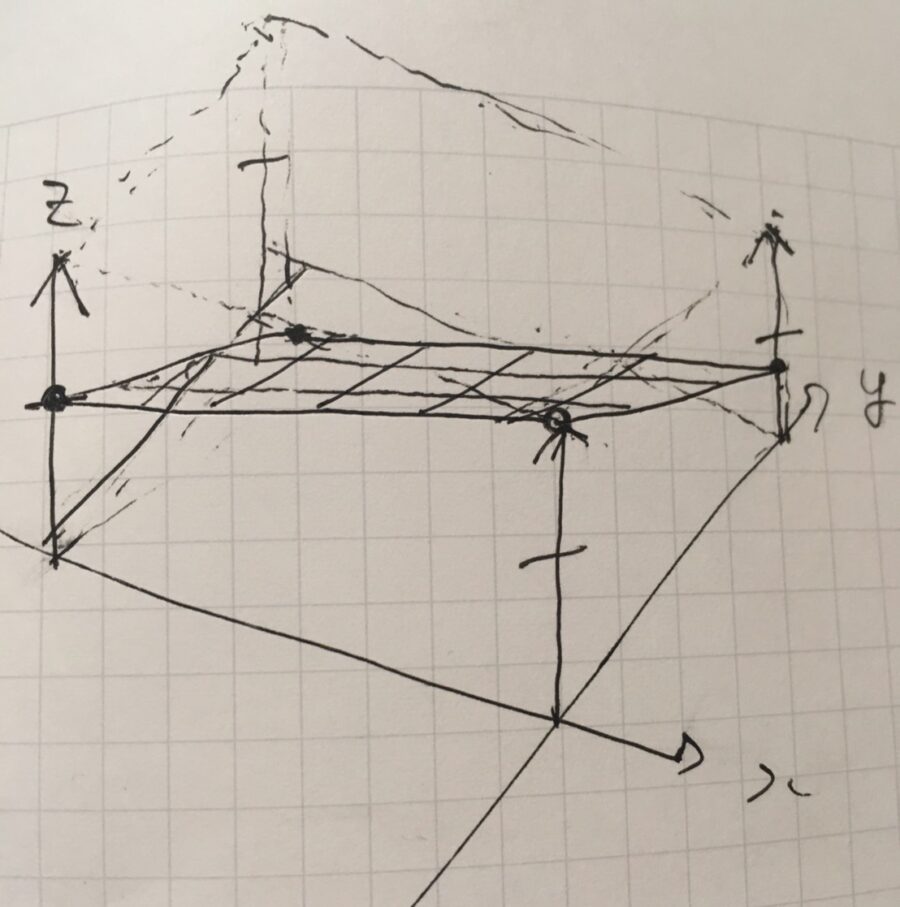
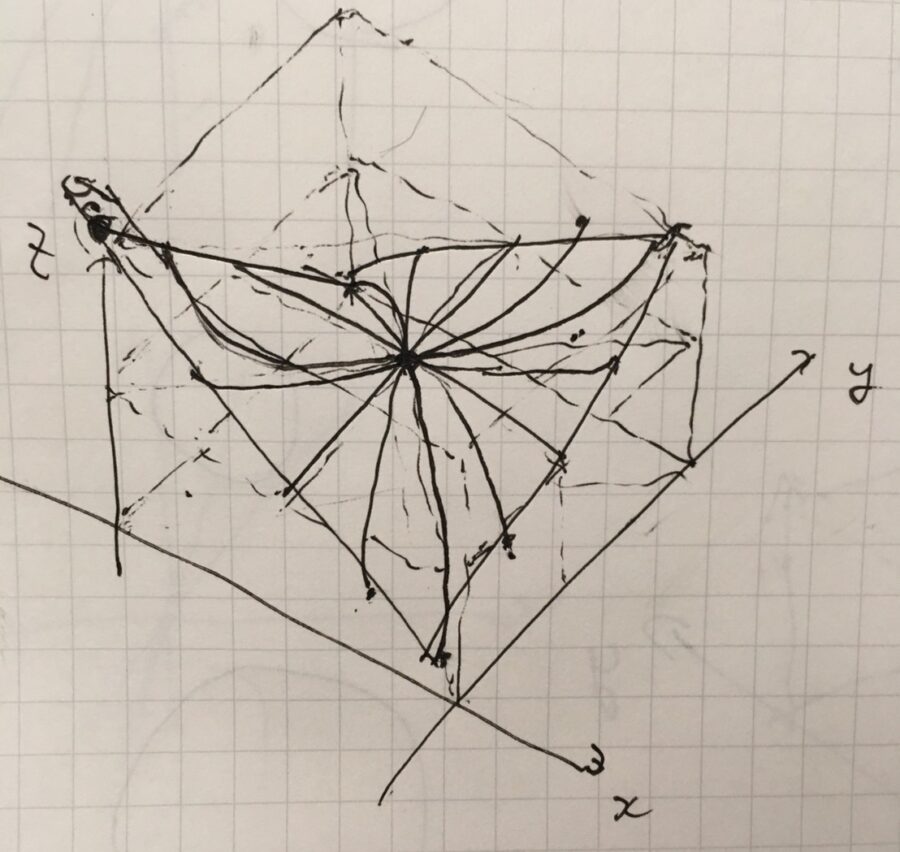
このグラフは、次の要領で作成しました。まず、\((x,y)\)軸を描き、そして\(z\)軸を一箇所に描きます。そしてその\(z\)軸の矢印を、\(x,y\)軸それぞれの軸に並行に移動させ、同じ長さのまま描きます。\(z\)が同じ高さの点をつないでいくことで、外側の枠組みとなる直方体(点線)が描けますね。
その後、一番左の\(z\)軸の真ん中のあたりから出発し、関数のグラフを描き始めます。\(x\)軸方向には直線で増加、\(y\)軸方向には直線で減少、傾きは\(y\)の方が\(-3\)とやや急に描きます。すると、4つの\(z\)軸上の点、それを結ぶ線によって、空間内にひとつの平面が描けました。
一般に、\(f(x,y)=ax+by\)のグラフは平面になります。
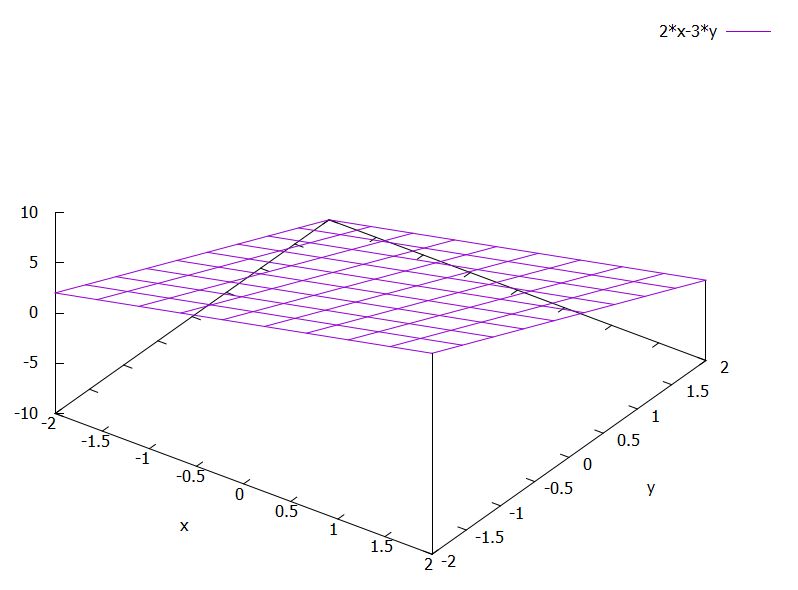
コンピュータ(gnuplot)を使うと、簡単にグラフが描けます。
さて、関数のグラフを描くために使った重要な情報は、何でしょうか。それは関数の傾きでした。今回の場合、\(x\)軸方向、\(y\)軸方向、2つの傾きがありました。
こうした\(x\)軸方向、\(y\)軸方向への接線の傾きを取り出すのが、偏微分(partial differentiation)です。特定の1つの変数に注目した微分で、偏微分して得られる関数を偏導関数(partial derivative)と呼びます。
\[ \begin{aligned}\frac{\partial f}{\partial x}(x,y):=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{h}\end{aligned} \]
\[ \begin{aligned}\frac{\partial f}{\partial y}(x,y):=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}{h}\end{aligned} \]
前者を\(x\)に関する偏微分、第1変数に関する偏微分、後者を\(y\)に関する偏微分、第2変数に関する偏微分と呼びます。
\(f_1(x,y)=2x-3y\)ならば、\(\frac{\partial f}{\partial x}(x,y)=2\)、\(\frac{\partial f}{\partial y}(x,y)=-3\)とそれぞれの傾きが取り出されます。
\(x\)について偏微分するときは、\(y\)は固定された定数として考えるのと同じで、定数項の\(-3y\)は微分すると0で消えます。\(y\)についての偏微分なら、\(x\)を固定された定数として考えるわけです。
(偏微分は\(f_x,f_y\)と略記されることもあります。また、文脈によっては、\(f_x\)が第一変数に関する偏微分を表すとは限らないことにも注意しましょう。\(f(t,x)\)という変数を考えるならば、\(f_x\)は第2変数に関する偏微分です。)
二次曲面のグラフ
1次関数に次いで単純な関数としては、2次関数\(f(x)=x^2\)がありました。
今回は、2変数の2次関数によって表される二次曲面(quadric surface)のグラフをいくつか描いてみましょう。
\(f_2(x,y):=x^2+y^2\)とします。\(f_2(x,0)=x^2\)、\(f_2(0,y)=y^2\)であり、点\((0,0)\)を中心とした、放物線のグラフを組み合わせたようなグラフになることが読み取れます。
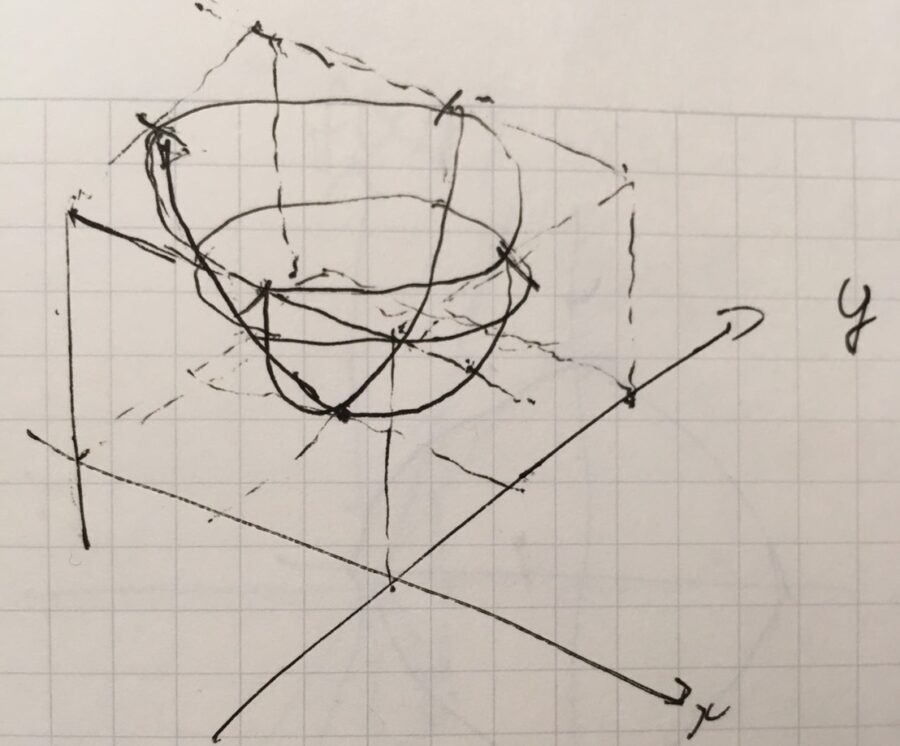
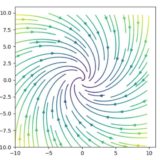
関数のグラフを読み取るときには、\((x,y)\)平面上に\(f\)の値が同じ場所をつないだ曲線を描くのも有効です。これを等高線(level curve, contour)と呼びます。標高が同じ場所を地図上でつないだ等高線、同じ気圧の地点をつないだ等圧線のイメージです。
例えば、\(f_2(0,1)=f_2(-1,0)=f_2(\sqrt{2}/2,\sqrt{2}/2)=1\)です。\(f_2(x,y)=x^2+y^2=c\)を満たす\(x,y\)を考えれば、それが円周になることがわかりますね。これを図示したのが次の画像です。
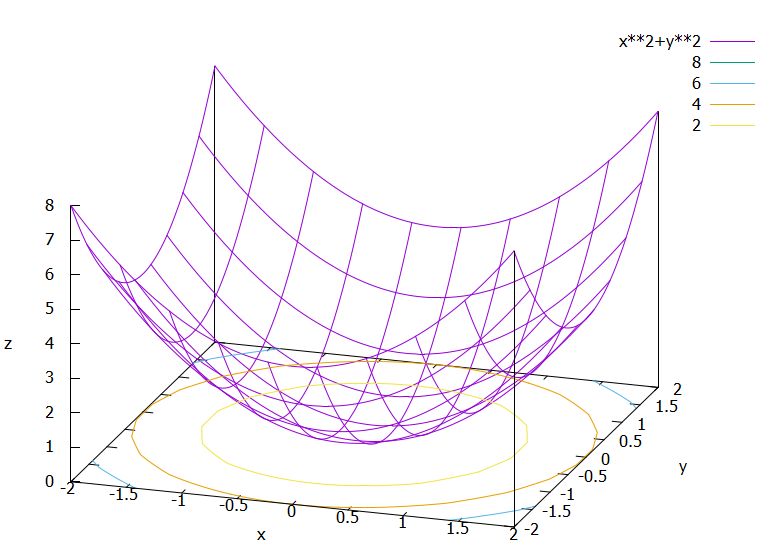
この曲面は、回転放物面と呼ばれます。\(x^2,y^2\)に正の係数がかけたものが、一般に楕円放物面(elliptic paraboloid)と呼ばれるものです。放物面は、外から音や光が入り込むとき、その焦点へ集中するという性質があり、パラボラアンテナや望遠鏡で利用されています。
また、偏微分を使えば、ある点で曲面に接する平面、接平面(tangent plane)が描けます。
\[ \begin{aligned}\nabla f:=\mathrm{grad} f:=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\end{aligned} \]
というベクトルを定めると、これは点\(x,y\)で\(f\)のグラフに接するベクトルです。これを\(f\)の勾配(gradient)ベクトルと呼びます。
\(f_2\)の点\(1,1\)における接平面を求めてみましょう。一般に\(\nabla f_2(x,y)=(2x,2y)\)なので、\(\nabla f_2(1,1)=(2,2)\)です。したがって、接平面を表す関数は\(g_2(x,y)=2(x-1)+2(y-1)+2\)です。実際、次の画像のように接しています。
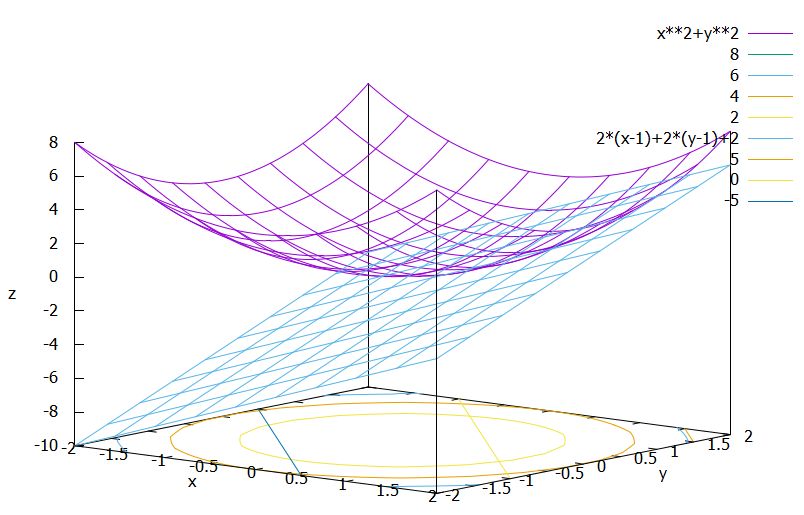
一般には、\(f\)の点\((a,b)\)における接平面の方程式は、\(g(x,y)=f_x(a,b)(x-a)+f_y(a,b)(y-b)+f(a,b)\)となりますね。1変数の場合の接線の方程式を思い出すと、\(f'(a)(x-a)+f(a)\)で、よく似ていますね。
(\(f(x,y)\)の\((a,b)\)における接平面は、勾配ベクトル\(\nabla f(a,b)\)により張られる線形空間を並行移動させたものとも言えます。)
参考:実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に
別の二次曲面の例を考えましょう。\(f_3(x,y)=x^2-y^2\)です。
これは\(y=0\)では\(x^2\)ですが、\(x=0\)では\(-y^2\)と、放物線の向きが軸によって入れ替わっています。また、\(x=y,x=-y\)上では常に値が0です。原点を通る2つの放物線と、縁(ふち)の放物線を意識すると、グラフにしやすいです。
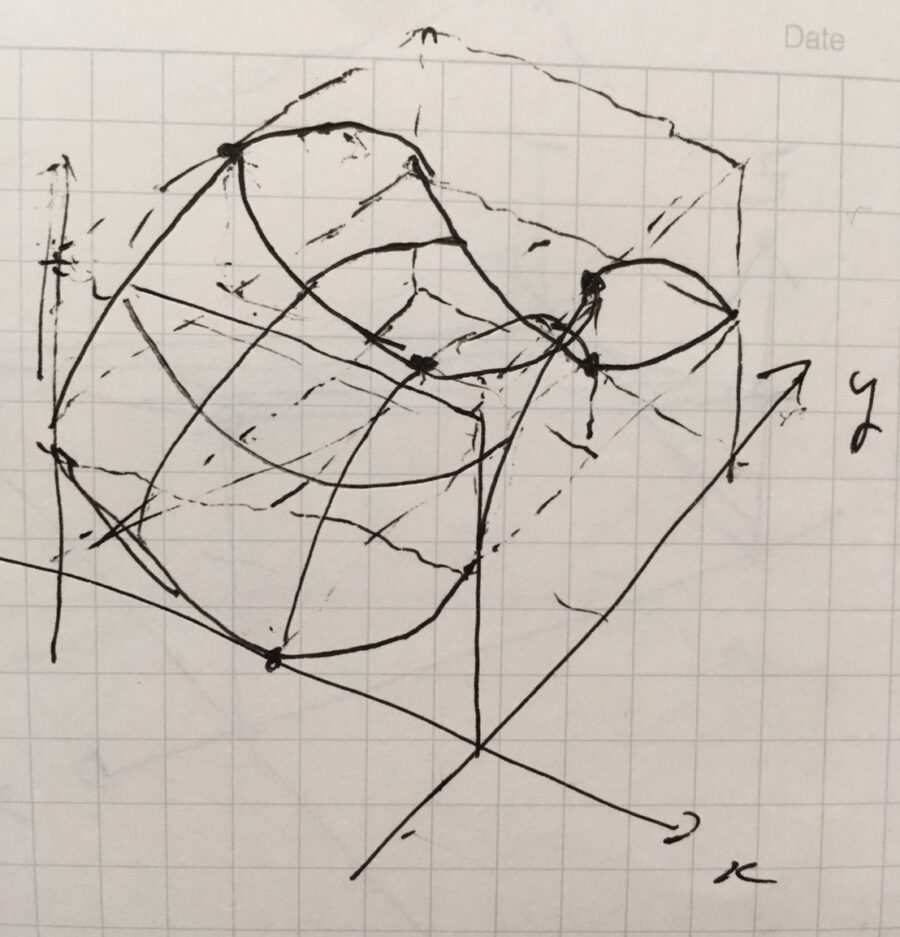
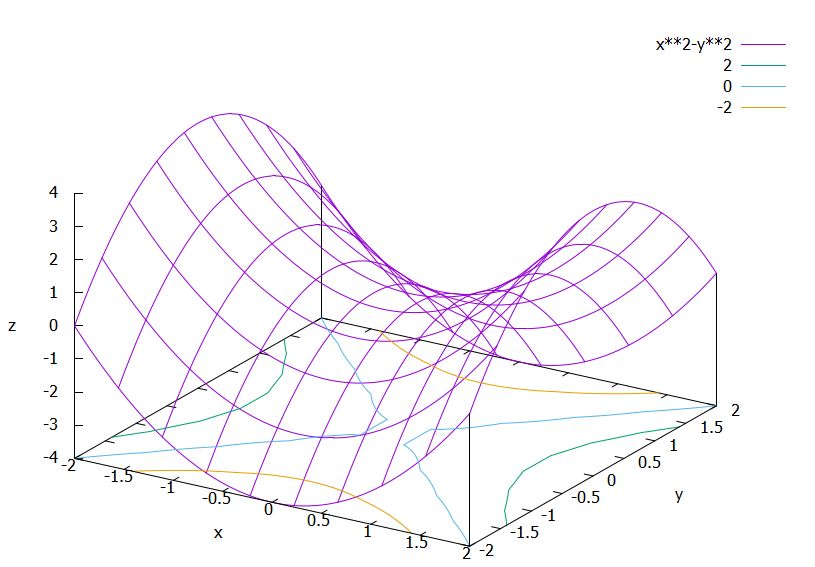
この曲面は、双曲放物面(hyperbolic paraboloid)、またはサドル面(saddle surface)と呼ばれます。馬に座るための椅子である鞍(サドル)によく似た形ですね。
点\((0,-1)\)における接平面を求めてみましょう。\(\nabla f_3(x,y)=(2x,-2y)\)で、\(\nabla f_3(0,-1)=(0,2)\)なので、求める平面は\(g_3(x,y)=2(y+1)-1\)です。

最後に、\(f_4(x,y)=xy\)なる二次曲面を考えてみましょう。
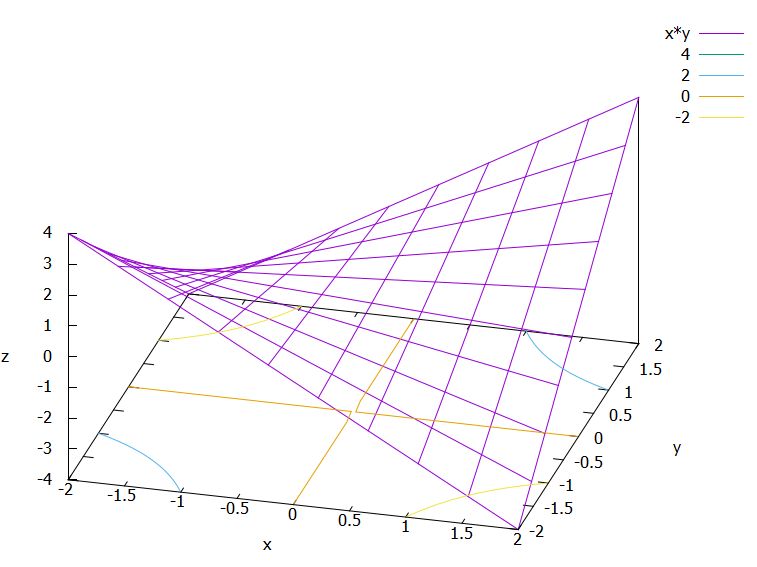
これは\(y=x\)上では\(x^2\)で、\(y=-x\)上では\(-x^2\)になっています。また、\(x\)軸に並行な面、\(y\)軸に並行な面では、例えば\(f_4(x,2)=2x\)と直線になっています。
これは先ほどの双曲放物面に似ていますね。ただし、原点を通り\(x\)軸、\(y\)軸方向に進むグラフ上の点は直線です。また、\(x\)軸、\(y\)軸に並行な切断面では、切断の位置に応じた傾きの直線となっています。
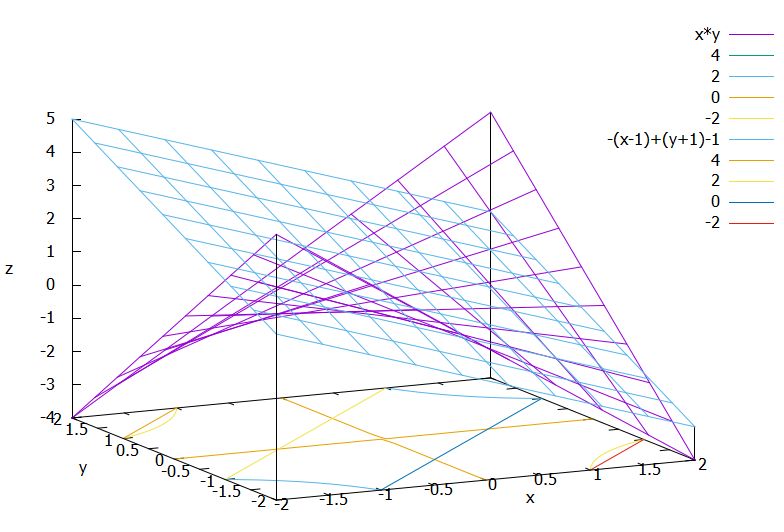
\((1,-1)\)における接平面を計算してみましょう。\(\nabla f_4(x,y)=(y,x)\)で、\(\nabla f_4(1,-1)=(-1,1)\)なので、\(g_4(x,y)=-(x-1)+(y+1)-1\)です。
ここまで、具体的な2変数関数の偏導関数を求めて接平面を描きましたが、この方法は一般の多変数関数に通用するわけではありません。実は、\(x,y\)について偏微分可能ですが、接平面が存在しない例があります。より一般に、接平面が存在する条件は、全微分可能性と呼ばれます。

偏微分可能性は、特定の方向の接線の存在しか見ていないわけです。ただし、偏導関数が存在し、かつ偏導関数も連続ならば、全微分可能となり、先ほどまでの議論と同様接平面が求まります。こういう関数を\(C^1\)級といいます。このあたりの話は、別の記事で紹介するかもしれません。
偏微分の応用先
今回は、簡単な2変数関数(平面、二次曲面)を例に、グラフの描き方、偏微分と接平面、等高線について紹介しました。
偏微分は、多くの現象を説明するために用いられる偏微分方程式に応用されます。時間\(t\)と場所\(x\)で、熱や波の変位など1次元的な量\(u(x,t)\)を考えれば、2変数関数や多変数関数が登場します。偏微分を使って表される等式を満たす多変数関数を求めるのが、偏微分方程式です。
参考:なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に、波の重ね合わせの原理はなぜ成り立つ? 波動方程式入門
また、輸送コストなど何か目標となる数値を多変数関数と表し、その最大値・最小値などの極値を求める問題は、極値問題、または最適化問題と呼ばれます。1変数のときに微分=0となる点を調べたように、多変数でも偏微分を用いてその極地を調べることができます。ラグランジュの未定乗数法と呼ばれる方法は、別の記事で紹介するかもしれません。
今回の例を通して、2変数関数の視覚的イメージや、その偏微分の扱い方を身近に感じられたでしょうか。関数の切断面を考えたり偏微分してみたりすることで、グラフとそれをよく近似する接平面が思い浮かべられると良いと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
実数空間、線形結合、線形部分空間、次元とは何か:2次元を例に