どうも、木村（@kimu3_slime）です。
微積分学や線形代数学において、多次元の関数は重要です。高校数学では、ベクトルと関数を結びつけることをあまりしなかったのではないでしょうか。
今回はその導入例として、曲線を1変数ベクトル値関数として表し、その微分を計算してみます。
2次元空間内の曲線
平面\(\mathbb{R}^2\)上の円を考えてみましょう。
半径1の円は、\(x^2+y^2=1\)という方程式を満たす点\((x,y)\)の集まりです。
この円上のある点\((a,b)\)における接線を求めたいときには、どうすれば良いでしょうか？ 高校数学では、点と直線の距離の関係を使い、\(ax+by=1\)を求めたかと思います。
曲線のパラメータ表示、1変数ベクトル値関数
微分の考え方を使えば、より一般的に考えやすくなります。
円を次のように、動きがあるように捉え直しましょう。\(t\)を時間のようなパラメータと考えます。\(t=0\)のとき\((0,1)\)から出発して反時計回りに出発し、\(t=\pi\)で\((0,-1)\)へ、\(t=2\pi\)で\((0,1)\)と一周してくる対応関係を考えてみます。
それは、\(c_1 (t):=(\cos t, \sin t)\)という関数です。\(t\)に適当な値を代入して、\(c_1(t)\)が円のどの位置に対応しているか描いてみてください。
\(c_1\)は、実数\(t\in \mathbb{R}\)に対して、ベクトル\((\cos t, \sin t) \in \mathbb{R}^2\)を対応させています。一般に、関数\(c:\mathbb{R} \to \mathbb{R}^N\)を、1変数のベクトル値関数（vector valued function）と呼びます。
また、特定の変数\(t\)によって表された曲線は、パラメータ付けされた曲線（parametrized curve）と呼びます。平面上の点の集まりと考えると2次元的ですが、今回のようにパラメータで表せていれば変数は1次元で済みますね。パラメータが2次元になれば、曲面を表すことができます。
円を動く点の軌跡として捉える考え方は、物理学、バネの運動方程式にあらわれてきます。
参考：サイン、コサインは何の役に立つ？ バネの振動と三角関数、「運動」をイメージすればわかる、微分と積分入門、方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
曲線の微分、接ベクトル
曲線\(c(t)\)は1変数の関数なので、\(t\)についての微分を考えることができます。円の曲線ならば、
\[ \begin{aligned}\frac{dc_1}{dt} (t):=(\frac{d}{dt}\cos t, \frac{d}{dt}\sin t)=(-\sin t, \cos t)\end{aligned} \]
です。これを曲線の接ベクトル(tangent vector)、または速度ベクトル(velocity vector)と言います。矢印の向きは真逆、かつ複数の円が描かれてしまっていますが、次のようなイメージです。
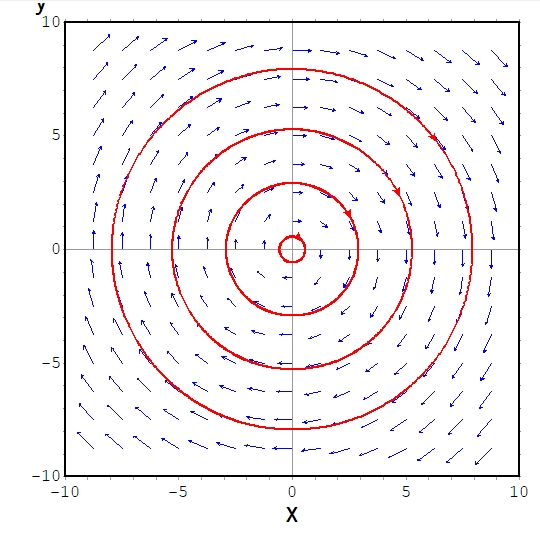
接ベクトルは、（並行移動すれば）常に曲線に接しています。つまり、円上の点\((\cos t, \sin t)\)を通る接線の傾きは、\((-\sin t, \cos t)\)と求められるわけです。シンプルですね。
楕円
円のパラメータ表示の式を少し変化させれば、楕円の方程式になります。
\[ \begin{aligned}c_2(t):=(2\cos t, \sin t)\end{aligned} \]
は、次のようなグラフです。
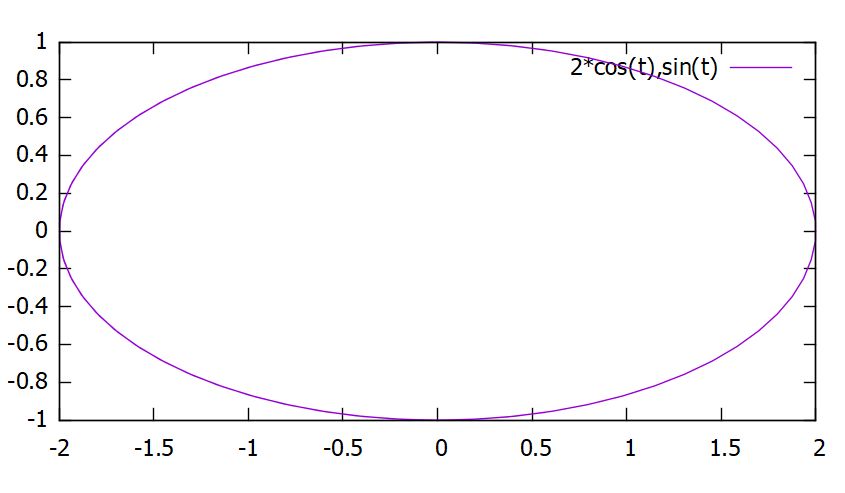その接ベクトルは、\(c_2(t)=(-2\sin t, \cos t)\)で、\(x\)軸方向に2倍に伸びていることがわかりますね。
アルキメデスの螺旋
別のケースを考えてみましょう。
\[ \begin{aligned}c_3(t) = (t \cos t, t\sin t)\end{aligned} \]
で表される曲線を、アルキメデスの螺旋と呼びます。円や楕円では\(t=0,2\pi\)で戻ってきましたが、こちらは同じ値にならずに進んでゆきます。
時刻\(t\)における原点からの距離は\(t\)であり、時間が経つにつれ原点から離れていきます。そして三角関数によって回転運動をしていますね。
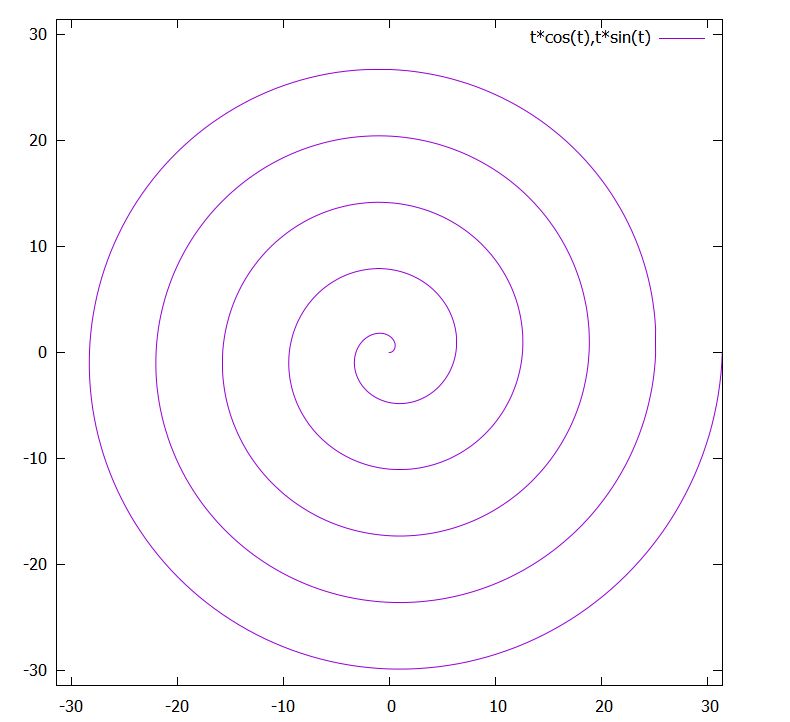
蚊取り線香のような形をしていますね。接ベクトルは、\(\frac{dc_3}{dt} = ( \cos t- t\sin t, \sin t+ t \cos t)\)です。
アルキメデスの螺旋は、時刻\(t\)における原点からの距離は\(t\)という式、つまり極座標による表示\(r = \theta\)の方がシンプルかもしれません。
3次元空間内の曲線
曲線のパラメータ表示において、取りうる値を3次元のベクトルにすれば、\(\mathbb{R}^3\)における曲線、空間曲線が描けます。
\[ \begin{aligned}c_4 := (\cos t, \sin t, t)\end{aligned} \]
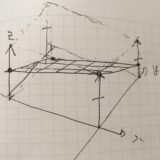
とすれば、\(x,y\)平面では円的に動きながら、\(z\)軸の正の方向へ進んでゆきます。この曲線は、つるまき線と呼ばれるものです。
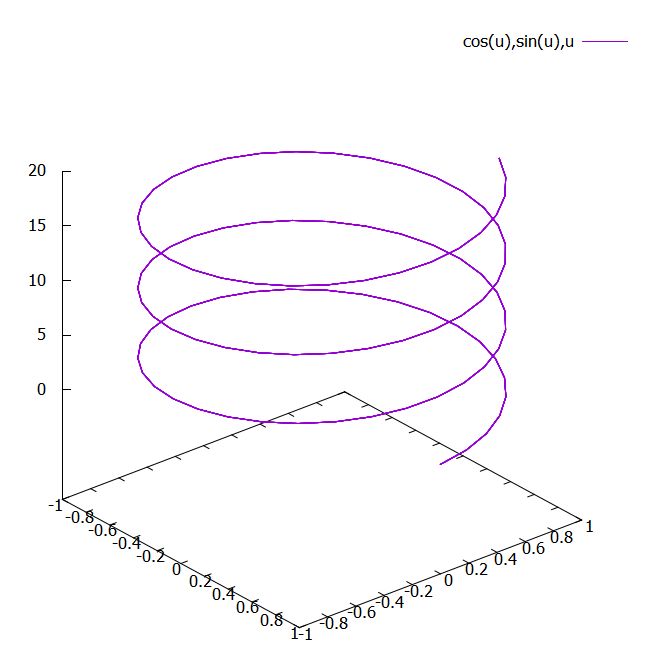
その接ベクトルは、\(\frac{dc_4}{dt}=(-\sin t, \cos t, 1)\)ですね。
まっすぐ進んでいた荷電粒子が一様な磁場に入ると、ローレンツ力によって、このような円運動、螺旋運動（サイクロトロン運動）をすることが知られています。
今回は、ベクトルと関数を組み合わせる考え方の例として、曲線のパラメータ表示、その微分（接ベクトル、速度ベクトル）について紹介しました。
曲線の積分をすることで、曲線の長さ、弧長を求めることができます。楕円の弧長は、定義はできますが、初等関数で表すことができず、楕円積分として知られています。
また、今回は1回微分のみ考えましたが、2回微分を考えることで、曲線の曲がり具合、曲率というものを考えることができます。曲線や曲面の幾何学的な性質を微分を使って調べる分野は、微分幾何学と呼ばれています。
ベクトルと関数を組み合わせる考え方は、いきなりだと難しいと思うので、今回紹介した曲線のような、2、3次元の簡単なケースから勉強してみてはいかがでしょうか。
木村すらいむ（@kimu3_slime）でした。ではでは。
裳華房
売り上げランキング: 94,864
こちらもおすすめ
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
