どうも、木村(@kimu3_slime)です。
今回は、古典論理の目的、妥当な推論とは何か、カテゴリー的命題とクラスについて解説します。
古典論理と妥当な推論

アリストテレス
古典論理(classical logic)は、古代ギリシャの哲学者アリストテレスによって築かれた論理学の体系、もといそれを引き継いだものを指します。それはアリストテレス的論理学(Aristotelian logic)、伝統的論理学(traditional logic)とも呼ばれます。
論理学を形容する言葉で、「アリストテレス的」とつけられるくらい、彼の論理学の完成度は高かったのでしょう(もちろん彼の後、特に近代で発展があったわけですが)。彼はそれを『オルガノン』と呼ばれる本にまとめ、その内容は
『範疇論』、『命題論』、『分析論前書』『分析論後書』、『トピカ』、『詭弁論駁論』
でした。オルガノンは道具を意味するラテン語で、論理、すなわち思考のツールを意味したものでしょう。
古典論理の目的は、「適切な」推論(argument)とそうでない推論を区別することです。
そもそも推論とは、いくつかの前提となる命題から結論を導くことでした。
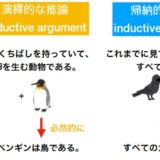
推論には前提と結論の結びつきの強さによって、帰納的推論と演繹的推論の2種類ありました。論理学では主に前提から結論が必ず導かれる(または導かれない)推論、すなわち演繹的な推論を対象にします。
参考:論理学の考え方、命題、主張、仮定、結論とは何か?、「演繹的・帰納的」な推論の定義、違いを、具体例を交えて解説
そして正しい前提から正しい結論が導かれるような演繹的推論のことを、妥当な推論(valid argument)と言います。正しい前提から間違った結論が得られるものが、妥当でない推論(invalid argument)です。
すなわち、論理学の主な目的は、妥当な推論と妥当でない推論を見分けることです。そして特に古典論理では、カテゴリー的命題と呼ばれる概念を対象に、典型的な推論である三段論法の妥当性を調べます。
(『オルガノン』の『範疇論』『命題論』はカテゴリー的命題、『分析論前書』『分析論後書』は三段論法の分析に対応すると言えるのではないでしょうか。カテゴリーは日本語では範疇 はんちゅう とも言います。)
あえて「古典」論理学と呼んでいるのは、近代論理学(modern logic)と呼ばれる記号論理学(symbolic logic)と対比させているからです。記号論理学はアリストテレスの論理学と全くの別物というわけではなく、それを記号化させ洗練させたものと言えます。
(数理論理学の立場でも「古典論理」という用語があります。それは二値論理学、ブール論理などの近代論理学を指して古典論理と呼ぶもので、今回紹介した「古典論理」とは少し意味が異なります。)

カテゴリー的命題とクラス
古典論理学では、カテゴリー的命題と呼ばれる命題を基本単位とし、それを使った三段論法の妥当性を考えます。例を見てみましょう。
すべての哺乳類は恒温動物である。
恒温動物であるトカゲはいない。
したがって、すべてのトカゲは哺乳類ではない。
これは三段論法で、どうやら妥当な推論に見えます。3つの文、ひとつひとつがカテゴリー的命題です。
その定義のために、まずクラス(類 class)という概念を考えます。クラスとは、ある特定の特徴を持つもの(object)の集まりのことです。数学で言う集合(set)によく似ていますね。クラスは、カテゴリーという概念とほぼ同義です。
そしてカテゴリー的命題(categorical proposition)とは、S、Pをクラスとして、「すべてのSはPである」「あるSはPでない」といったように、2つのクラスの間の関係を述べる命題です。
上に挙げた例では、哺乳類、恒温動物、トカゲがクラスです。これらのクラス間の包含関係、あるいは排他関係を述べているので、これらはカテゴリー的命題です。さらに、カテゴリー的命題を使った三段論法の例でもあります。
カテゴリー的命題は、主に4種類に分類されます。「すべてのSはPである」「すべてのSはPでない」「あるSはPである」「あるSはPでない」、これらをカテゴリー的命題の標準形と呼びます。この話は、長くなるので別の記事で紹介。
今回は、アリストテレス的論理学、古典論理を紹介しました。それには妥当な演繹的推論を見出すという目的があります。そのために、共通の性質を持ったものの集まり、すなわちクラスを考え、そこからカテゴリー的命題、それを使った三段論法を分析していくのです。まずはカテゴリー的命題の理解から出発していきましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Introduction to Logic (English Edition)
参考文献
Copi, Cohen, MacMahon “Introduction to Logic”