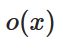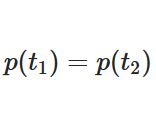どうも、木村(@kimu3_slime)です。
高校の物理学では、力学的エネルギー保存の法則を習うと思います。
物体に保存力のみが働く場合、\(K\)を運動エネルギー、\(U\)を位置エネルギーとして、
\[ \begin{aligned}K+U=E\end{aligned} \]
は一定。つまり、どんな物体の運動を考えても、\(E\)の値は運動の前後で変化しない。
例えば、(摩擦を考えない)落体の運動ならば、\(K=\frac{1}{2}m v^2\)、\(U=mgh\)となるのでした。
この力学的エネルギー保存の法則は、微積分を使って、ニュートンの運動法則(運動方程式)から導くことができます。今回はそれを紹介します。
前提知識:高校レベルの微積分。「運動」をイメージすればわかる、微分と積分入門
力学的エネルギー保存の法則を微積分で証明する
言葉の確認
まず、言葉の確認をしましょう。
物体の質量を\(m\)、時刻\(t\)における物体の位置を\(x(t)\)、すなわち時間の関数として表すことにします。このとき、速度と加速度は
\[ \begin{aligned}v(t)= \frac{dx}{dt}(t),\quad a(t)= \frac{dv}{dt}(t)= \frac{d^2x}{dt^2}(t)\end{aligned} \]
と定義されるのでした。また、物体に加わる力を\(F(x,v,t)\)とします。
運動方程式は
\[ \begin{aligned}m a(t) = F(x,v,t)\end{aligned} \]
です。
一次元の場合
簡単のため、一次元の運動を考え、力学的エネルギー保存の法則を導いてみましょう。
力学的エネルギー保存の法則は、「物体に保存力のみが働く場合」という仮定を考えています。
力\(F(x,v,t)\)が保存力であるとは、\(F=f(x)\)と、力が\(x\)のみの関数として表されることと定義されます。力が、物体の速度\(v\)や運動の時間\(t\)に依存しないとも言い換えられます。
例えば、重力\(F=-mg\)やバネの復元力\(F=-kx\)は保存力です。一方、摩擦力は、常に進行方向と逆に働く、すなわち速度\(v\)に依存するので、保存力ではありません。
では、保存則を導きましょう。運動方程式の両辺に速度\(v\)をかけて、両辺を\(t\)について\(0\)から\(t_1\)まで積分すると、
\[ \begin{aligned}\int _0 ^{t_1} mav dt = \int_0 ^{t_1} f(x)v dt \end{aligned} \]
です。\(\frac{d}{dt}(\frac{1}{2} m v^2)= m \frac{dv}{dt} v= mav\)なので、左辺の積分は
\[\begin{aligned} \int _0 ^{t_1} mav dt &= [\frac{1}{2} m v^2]_{t=0} ^{t=t_1} \\ &= \frac{1}{2} m v^2(t_1) – \frac{1}{2} m v^2(0) \end{aligned} \]
となります。
一方、右辺の積分はどうなるか。\(t=x \)と変数変換すると、\(\frac{dx}{dt}=v\)なので、
\[\int_0 ^{t_1} f(x)v dt = \int_ {x(0)} ^{x(t_1)} f(x)dx \]
です。右辺は位置\(x\)のみによって決まる量で、\(U(x):=- \int _0 ^x f(s)ds\)と置くと、
\[\begin{aligned} \int_ {x(0)} ^{x(t_1)} f(x)dx &= \int _{x(0)} ^{0} f(s)ds + \int _0 ^{x(t_1)} f(s)ds \\ &= – \int _0 ^{x(0)} f(s)ds + \int _0 ^{x(t_1)} f(s)ds \\ &= U(x(0)) -U(x(t_1)) \end{aligned} \]
です。よって、左辺の積分=右辺の積分の式に結果を代入し、整理すれば、
\[ \begin{aligned} \frac{1}{2} m v^2(0) +U(x(0))= \frac{1}{2} m v^2(t_1) +U(x(t_1))\end{aligned} \]
となります。ここで運動エネルギーを\(K(x)=\frac{1}{2} m v^2(x)\)、位置エネルギー(ポテンシャルエネルギー)を\(U(x)=- \int _0 ^x f(s)ds\)と定義します。
運動エネルギーと位置エネルギーの和(力学的エネルギー)は、時間\(t_1\)が経過しても変化しません。そして\(t_1\)は任意に選んだものなので、どんな運動を考えても、力学的エネルギーは保存されます。すなわち、力学的エネルギー保存則が証明されました。
証明全体を簡単にまとめましょう。
運動方程式の両辺に\(v\)をかけて、時間に関する積分を取る。すると、左辺からは運動エネルギーの変化分が登場する(そうなるために\(v\)をかけた)。右辺からは位置エネルギーの変化分が登場する(力\(F\)が保存力なので。)。この議論をまとめたものが、力学的エネルギー保存則ですね。
多次元の場合(簡単に)
今回は1次元の場合を考えましたが、多次元(2,3次元)でも同様に示せます。\(a=(a_1,a_2,a_3)\)、\(F=(F_1,F_2,F_3)\)とベクトルで表すと、運動方程式は、
\[ \begin{aligned}m a_1 = F_1, ma_2 = F_2, ma_3 =F_3\end{aligned} \]
です。それぞれに\(v_1,v_2,v_3\)をかけて積分すれば、左辺を足し合わせて\(mv^2/2\)が出てきます。右辺は
\[ \begin{aligned}\int_0 ^{t_1} F_1 v_1 +F_2 v_2 + F_3 v_3 dt =\int _0 ^{t_1} F(x(t))\cdot v(t) dt\end{aligned} \]
です。右辺を、経路\(x(t)\)上の\(F\)の線積分と言います。この積分の値は、「同値」な曲線ならば変わりません。例えば、\(t\mapsto 2t\)と変数変換した(時間変化の速度を変化させた)としても、値は変わりません。ただし一般には、途中の経路\(x(t)\)が変われば、当然値が変わります。
そこで、2点を結ぶ経路によらずにこの積分の値が一定になるような力を考え、それを保存力と呼びます。このとき、始点と終点\(x(0),x(t_1)\)を結ぶ曲線を\(C\)として、
\[ \begin{aligned} W(x(0),x(t_1)):=\int _C F \end{aligned} \]
と置きましょう。\(W\)を力\(F\)が物体を\(x(0)\)から\(x(t_1)\)に動かすのにした仕事と呼びます。一次元ならば\(W= \int_ {x(0)} ^{x(t_1)} f(x)dx\)で、たしかに始点終点のみで決まっていますね。
適当に基準点を決めることで、\(W(x(0),x(t_1))= U(x(0))-U(x(t_1))\)とポテンシャルエネルギーを表せます。よって、
\[ \begin{aligned} \frac{1}{2} m v^2(0) +U(x(0))= \frac{1}{2} m v^2(t_1) +U(x(t_1))\end{aligned} \]
が言えました。仕事が経路に依存せず、始点と終点のみによって決まる力(保存力)を考えたのがポイントですね。
以上、力学的エネルギー保存の法則を、微積分学によって導出、証明する方法を紹介しました。
運動方程式が正しく(運動方程式にのっとった運動を考え)、保存力のみ働くならば、力学的エネルギー保存則は微積分を使って、数学的に(理論的に)証明されます。
「法則」とは言いますが、運動方程式が正しいときの当然の帰結であることが、今回の話から感じてもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
惑星の運動は数学的に「解けない」? 多体問題から力学系理論へ