どうも、木村(@kimu3_slime)です。
微積分学・解析学で登場する、関数のオーダー評価の記法、ランダウの記号の扱いと、そのテイラー展開への応用について解説します。
ランダウ記号の具体例、定義
関数のオーダー評価とは、ざっくり言えば、極限を取ったときの収束の速さがどれくらいかを表すものです。
三角関数、\(\sin x\)の\(x\to 0\)での収束の速さに注目してみましょう。テイラー展開によれば、次のように多項式の和として展開されます。
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}- \cdots \end{aligned} \]
参考:テイラー展開の展開式の覚え方、導き方、証明、なぜテイラー展開を学ぶ? 単振り子を例にわかりやすく解説
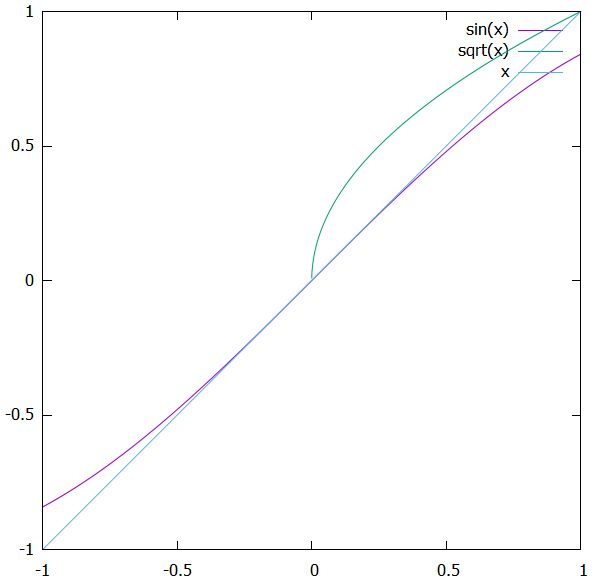
このとき、\(x\to 0\)における\(\sin x\)の\(0\)への収束は、\(g(x)=\sqrt{x}\)より速く、\(h(x)=x\)と同じ速さに見えます。
2つの関数の収束の速さを比べるには、その比の極限の値を調べれば良いです。今回は、
\[ \begin{aligned}\lim _{x\to 0} \frac{\sin x}{ \sqrt{x}} =0\end{aligned} \]
\[ \begin{aligned}\lim _{x\to 0} \frac{\sin x}{ x} =1\end{aligned} \]
です。
上側の事実を、\(0\)において\(\sin x\)は\(\sqrt{x}\)に比べて無視できるほど小さい、または高次の無限小であるといい、\(\sin x = o(\sqrt{x})\quad(x\to 0)\)と表します。左側の関数が、右側の関数に比べてより速く0に近づくわけです。
下側の事実を、\(\sin x\)は\(x\)によって押さえられると言い、\(\sin x = O(x)\quad( x\to 0)\)と表します。左側の関数が、右側の関数と同じくらいの速さで収束しています。
より一般には、\(f(x)=o(g(x))\quad (x\to a)\)、\(f(x)=O(h(x))\quad (x\to a)\)とは、
\[ \begin{aligned}\lim _{x\to a} \frac{f(x)}{ g(x)} =0\end{aligned} \]
\[ \begin{aligned}(\exists C,\varepsilon >0)(\forall x \in \mathbb{R}) x\neq a, |x-a|<\varepsilon \Rightarrow | \frac{f(x)}{ h(x)} | \leq C\end{aligned} \]
が成り立つことと定義します。
このように、関数の収束の速さを\(o,O\)によって表す方法を、ランダウの記法(Landau notation)、または漸近記法(asymptotic notation)と言います。また、\(o\)はスモールオー(Little-o notation リトルオー、またはスモールオーダー)、\(O\)はビッグオー(Big O notation、単にオーダー)などと呼ばれます。
また、ランダウの記号は極限の振る舞いを表したもので、\(o(h(x))\)が特定の関数を表しているわけではないことに注意してください。
例えば、\(\sin x = o(\sqrt{x})\quad (x\to 0),2\sqrt{x}= o(\sqrt{x})\quad (x\to 0)\)で、”右辺が等しい”といって、\(\sin x = 2\sqrt{x}\)などが成り立つわけはありません。
単に\(o(h(x))\)と書かれた項があったら、「\(f(x)=o(h(x))\)と表せる関数\(f\)が存在する」という意味なのだと読み取りましょう。誤解を減らす意味では、等号を使わずに、\(f \ll h\)と非対称な記号を使った方が良いかもしれません。
また、同じランダウ記号を使っていても、考えている極限がどこなのかを意識してください。\(x\to a\)なのか\(x\to \infty\)なのかによって、意味は異なります。\(\sin x = o(\sqrt{x})\quad (x\to 0)\)であり、\(\sin x = o(x)\quad (x\to \infty)\)です。
多項式のスモールオーの扱い
スモールオー、特に多項式のスモールオー\(o(x^k) \quad( x\to 0)\)、\(o((x-a)^k)\quad (x\to a)\)は良く使います。
スモールオーの定義から、定数倍では変化しないですし、高い次数の項は低い次数にまとめられます。\(c\in \mathbb{R},l \leq k\)として、
\[ \begin{aligned}o(c x^ k)=o(x^k),\quad x^l + x^k = o(x^l)\\ \quad o(x^m)o(x^n)=o(x^{m+n}) \quad(x\to 0)\end{aligned} \]
が成立しています。
多項式のスモールオーを使えば、三角関数のテイラー展開は
\[ \begin{aligned}\sin x=x+ o(x) \end{aligned} \]
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ o(x^3) \end{aligned} \]
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}+o(x^5) \end{aligned} \]
と表されます。(ビッグオー記法だと、\(\sin x=x+ O(x^2)\)と1つ次数がずれることに注意しましょう )
テイラー展開における剰余項の扱い
テイラーの定理によると、\(f\)を\(n+1\)回微分可能な関数として
\[\begin{aligned} f(x)&=f(a)+f'(a)(x-a)+ \cdots \\ &+ \frac{f^{(n)}(a)}{n!}(x-a)^n + R_{n+1}(x) \end{aligned} \]
\[ \begin{aligned}R_{n+1}(x)=\frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\end{aligned} \]
を満たす\(c\in (a,x)\)が存在する。\(R\)を剰余項と呼ぶ。
と言えるのでした。剰余項は\((x-a)^n\)より高次の無限小なので、
\[\begin{aligned} f(x)&=f(a)+f'(a)(x-a)+ \cdots \\ &+ \frac{f^{(n)}(a)}{n!}(x-a)^n + o((x-a)^n) \quad(x\to a) \end{aligned} \]
と表されます。これは非常にシンプルですね。
先程の多項式のスモールオーの扱いと、基本的な関数のテイラー展開の式を覚えていれば、多くの関数のテイラー展開が簡単に求められます。
例えば、\(f(x)=e^{x \sin x}\)の原点におけるテイラー展開を\(x^6\)の項まで求めてみましょう。
まず、
\[\begin{aligned} x\sin x &= x(x- \frac{1}{6}x^3+\frac{1}{120}x^5+o(x^6))\\&=x^2 – \frac{1}{6}x^4+\frac{1}{120}x^6 + o(x^6) \end{aligned} \]
で、その2乗、3乗は
\[\begin{aligned} (x\sin x)^2 &= x^4 -\frac{1}{3}x^6 + \frac{1}{36}x^8 + o(x^6)\\ &= x^4 -\frac{1}{3}x^6 + o(x^6) \end{aligned} \]
\[(x\sin x)^3 = x^6 + o(x^6)\]
です。よって、
\[\begin{aligned} e^{x \sin x} &= 1 + x\sin x \\ & +\frac{1}{2} (x\sin x)^2 +\frac{1}{6}(x \sin x)^3+ o(x^6)\\ &=1 + (x^2 – \frac{1}{6}x^4+\frac{1}{120}x^6+o(x^6)) \\ &+\frac{1}{2}(x^4 -\frac{1}{3}x^6 + o(x^6))\\ &+\frac{1}{6}( x^6 + o(x^6))+ o(x^6)\\ &= 1 + x^2 +\frac{1}{3}x^4 +\frac{1}{120}x^6 +o(x^6)\end{aligned} \]
と求まりました。コンピュータでグラフを表すと、非常に良く近似できていることがわかります。
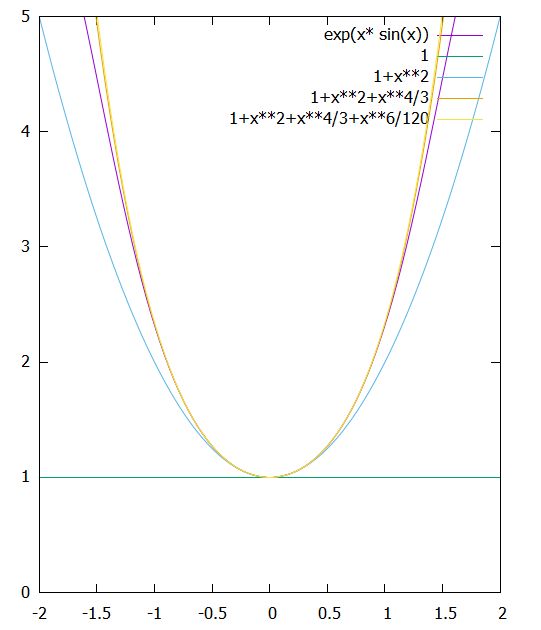
一般に、ある関数\(f\)を、特定の関数(主要項)とスモールオーの関数(剰余項)の和として表すことを、\(f\)の漸近展開(asymptotic expansion)と呼びます。
多項式による漸近展開がテイラー展開です。また、\(f(x)=b+ax+o(1),\quad (x\to \infty)\)としたとき、\(y=ax+b\)は漸近線と呼ばれます。
スモールオーやビッグオーは、多変数関数に対しても定義できます。
例えば、\(f(x,y)=x^2 +y^2 = o(|x|+|y|)\quad ((x,y)\to0)\)です。
そして、これは微分可能性の定義にも役立ちます。一変数関数\(f\)が微分可能であるとき、
\[ \begin{aligned}\lim _{h\to 0} \frac{f(x+h)-f(x)-f^{\prime}(x)h }{h}=0\end{aligned} \]
なので、
\(f(x+h)-f(x)= ch +o(h),\quad (h\to 0)\)を満たす\(c\)が存在する。
と言い換えられます。つまり、微分係数とは、テイラー展開の一次の項の係数です。逆に、多変数関数が微分可能であるとは、
\(f(x+h)-f(x)= ch +o(|h|),\quad (h\to 0)\)を満たす\(c\)が存在する。
と定義されるわけです。
今回は、三角関数を例にして、関数のオーダー評価、ランダウの記号の扱い方を紹介しました。
テイラー展開の剰余項のオーダーを把握し、近似式を作ったり、それによって極限を求めるのは解析学の基本的なテクニックです。ぜひ取得しておきましょう。
木村すらいむ(@kimu3_slime)でした。ではでは。