どうも、木村(@kimu3_slime)です。
Pythonで、平均、中央値、分散、相関係数などの統計量関数を作り、可視化する方法を紹介します。
statisticsモジュール、pandasモジュールにこれらは含まれますが、今回は統計学の勉強、統計量の意味の理解のため、定義式に戻って計算してみました。
平均、中央値、分散、標準偏差
\(x=(x_1,\dots, x_n)\)を調べたいデータとします。
この\(n\)個のデータの特徴を引き出すのが、種々の統計量(statistic)です。
最初に、定義とそのプログラム例を紹介しましょう。最後に、具体的なデータで統計量の値を計算します。
平均(mean)は、データの各成分を足しデータサイズで割ったものです。
\[ \begin{aligned}\mathrm{m}(x) = \frac{\sum_{i=1} ^n x_i}{n}\end{aligned} \]
Pythonの組み込み関数sumはデータの各成分の総和、lenはデータのサイズ\(n\)を求めてくれます。
1 2 3 | def mean(x): m = sum(x)/len(x) return m |
中央値(median)は、データの成分を小さい順に並び替えて、順番的に中央に来る成分の値です。
中央とは約\(n/2\)のこと。\(n\)が奇数のときはピッタリ中央が存在するのでその値を使います。\(n\)が偶数のときは、ピッタリ中央が存在しないので、中央2つの値の平均を使いましょう。
1 2 3 4 5 6 7 8 9 10 | def median(x): n = len(x) if n % 2 == 0: # データのサイズが偶数か奇数かで場合分け。 m1 = int(n/2) - 1 # 割り算の結果はfloatになる。リストに渡すためintにしておく。 m2 = int(n/2) med = (sorted(x)[m1] + sorted(x)[m2])/ 2 else: m = int((n+1)/2) -1 # リストのインデックスに気をつける med = sorted(x)[m] |
平均や中央値は、データで目立って見られる値を示すもので、代表値と呼ばれます。一方、データの散らばり具合を調べるにはどうしたら良いでしょうか。
もっとも簡単な量は範囲(range)で、データの最大値から最小値を引いたものです。
分散(variance)は、データの平均からのずれを測れる量で、データの散らばり具合を表します。
\[ \begin{aligned}\mathrm{v}(x) = \frac{\sum_{i=1} ^n (x_i – \mathrm{m}(x))^2} {n}\end{aligned} \]
偏差\(x_i – \mathrm{m}\)の二乗の平均とも言えますね。(二乗せずに足し合わせる式を考えると、常に0になってしまいます)
分散の平方根を、標準偏差(standard deviation)\(\mathrm{std}(x)\)と呼びます。
1 2 3 4 5 6 7 8 | def variance(x): d=0 for i in range(len(x)): d = d+ (x[i]-mean(x))**2 return d/ len(x) def std_deviation(x): return variance(x)**0.5 |
分子の和を取るために、for文による反復を用いました。
共分散、相関係数
2つのデータ\(x,y\)に規則性、特に線形的な関係があるかどうかを調べましょう。
次の量を、ピアソンの相関係数(Pearson correlation coefficient)と呼びます。
\[ \begin{aligned}\mathrm{cor}(x,y) = \frac{\mathrm{cov}(x,y)}{\mathrm{std}(x)\mathrm{std}(y)}\end{aligned} \]
分母は標準偏差の積ですが、分子は共分散(covariance)と呼ばれるものです。
\[ \begin{aligned}\mathrm{cov}(x,y) = \frac{\sum _{i=1}^n (x_i -\mathrm{m}(x))(y_i – \mathrm{m}(y))}{n}\end{aligned} \]
共分散の分子は、\(x,y\)それぞれの平均と成分の離れ具合を計算してかけたもので、符号付きで足し合わせていることになります。
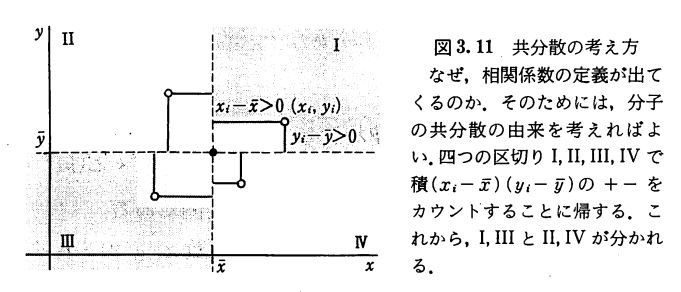
画像引用:東京大学出版会「統計学入門」 p.50
相関係数はその定義により、\( 0\leq |\mathrm{cor}(x,y)| \leq 1\)となります。0に近いときは相関関係がない、1に近いときは正の相関関係がある、-1に近いときは負の相関関係がある、と言うわけです。
(相関関係があることは、因果関係があることを意味しません。これは別の記事でいつか書くかと思います。)
1 2 3 4 5 6 7 8 | def covariance(x,y): c=0 for i in range(len(x)): c = c + (x[i]-mean(x))*(y[i]-mean(y)) return c/len(x) def correlation(x,y): return covariance(x,y)/ (std_deviation(x)*std_deviation(y)) |
平均、分散、標準偏差、共分散……と計算していけば、相関係数の計算で難しいことはありませんね。
具体例とその可視化
今までの関数を、具体的なデータを入れて使ってみましょう。
乱数の生成にrandomモジュール、可視化にmatplotlibを使います。
参考:random — 擬似乱数を生成する – Pythonドキュメント、1.4. Matplotlib: 作図 – Scipy Lecture Notes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | import random import matplotlib.pyplot as plt # 統計量の関数定義は省略 # データの定義。サイズは100。 x = list(range(100)) # [1,2,...,100]と1ずつ増えるだけ。 y = [] # 各成分が乱数で生成される。 for i in range(100): y.append(random.uniform(0,10)) # 乱数の範囲は0以上10以下。 print("mean",mean(x),mean(y)) print("median",median(x),median(y)) print("range",max(x)-min(x),max(y)-min(y)) print("variance",variance(x),variance(y)) print("standard deviation",std_deviation(x),std_deviation(y)) print("covariance,correlation",covariance(x,y),correlation(x,y)) fig = plt.figure() ax1 = fig.add_subplot(1,2,1) # 2つの図を同時に表示させる ax2 = fig.add_subplot(1,2,2) ax1.scatter(x,y) # 散布図を描く ax1.set_ylim(min(x),max(x)) # 図の縦横比を指定しておく ax2.hist(y,bins=20) # ヒストグラムを描く plt.show() |
その実行結果の例は次の通り。(乱数を使っているので、結果は毎回違います)
1 2 3 4 5 6 | mean 49.5 5.079925614730056 median 49.5 5.203983229024781 range 99 9.886029398927858 variance 833.25 8.439241826190585 standard deviation 28.86607004772212 2.9050373192423167 covariance,correlation 1.055292265240551 0.012584425032816747 |
\(x\)については平均と中央値が完全に一致していますが、\(y\)ではそうではありません。範囲、分散、標準偏差は\(x\)の方が明らかに大きいですね。
また、\(x,y\)の相関係数は約0.01で、ほとんど相関がないことがわかります。
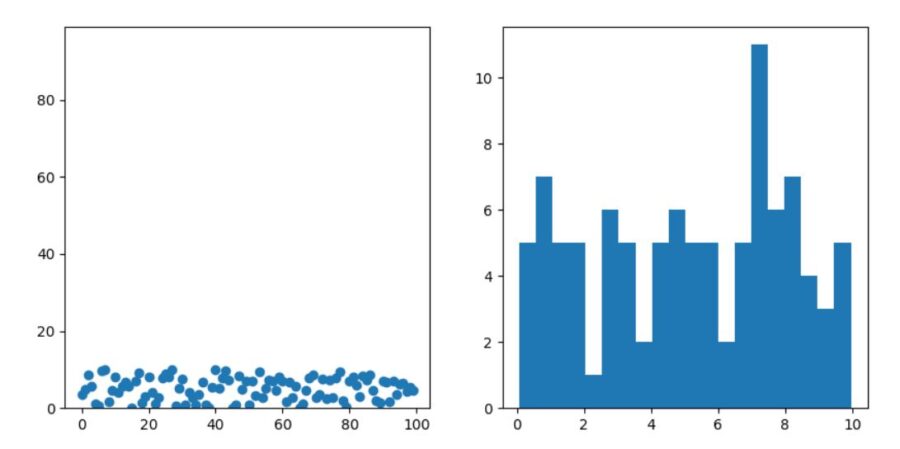
データ\(y\)について右側の図は、ヒストグラム(histgram)または度数分布(frequency distribution)と呼ばれます。横軸はデータの取りうる値を0~1,1~2,…,9~10といったように階級(class)に分けたもの。その階級ごとの\(y\)の成分の個数、すなわち頻度(frequency)が縦軸に棒グラフとして描かれているわけです。階級の個数、区切りの細かさはビン(bin)と呼ばれ、Pythonの描写でも指定できます。
データ\(x,y\)について左側の図は、横軸に\(x\)、縦軸に\(y\)を取り、\((x_i,y_i)\)をプロットしたもので、散布図(scatter plot)と呼ばれるものです。
少しだけデータを変えてみましょう。
y = sorted(y)として、yを小さい順に並び替えたデータでプログラムを実行してみました。
1 2 3 4 5 6 | mean 49.5 4.81187853591708 median 49.5 4.646541617092883 range 99 9.899290588913862 variance 833.25 8.431294905893543 standard deviation 28.86607004772212 2.9036692142689984 covariance,correlation 83.65471884208355 0.9980576841871588 |
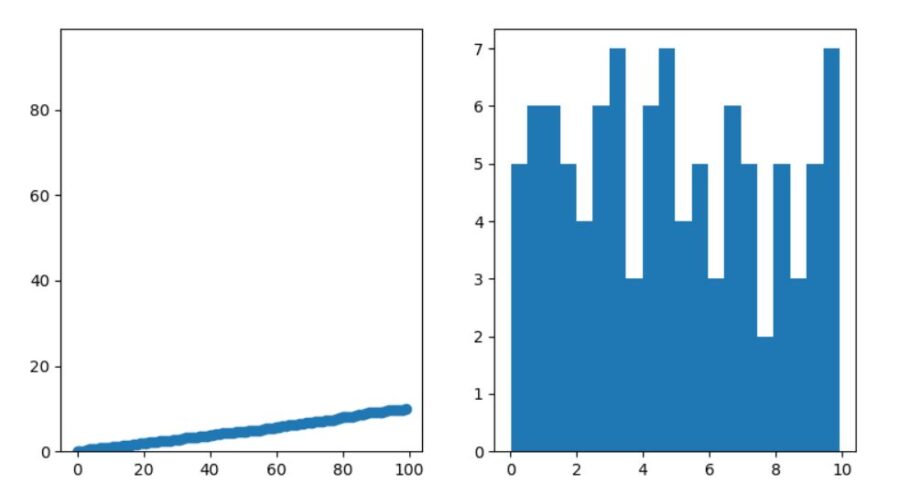
並び替えによって、\(x\)が増えるにつれ\(y\)が単調に増えるようになったことが、散布図からわかります。
相関係数は約1で、強い正の相関があることがきちんと示されていますね。(\(x,y\)に線形関係があるならば相関係数の大きさが約1になりますが、逆は必ずしも成り立たないことに注意)
冒頭で書きましたが、今回紹介した統計量はモジュールを使ってできあがったものをすぐ使うことができます。
しかし、定義式を理解しないまま使っても、数字は出せるでしょうが、その意味の理解は難しくなります。
Pythonとセットで統計を学びたいときは、今回紹介したように定義式に戻ってプログラムを書いてみてはいかがでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
オライリージャパン
売り上げランキング: 62,016
こちらもおすすめ
統計学の手法に違いはあっても対立はない 「9つの確率・統計学物語」レビュー
論理に関するド・モルガンの法則を真偽値の計算(プログラミング)で確かめる
「AならばB」は「Aでない、またはB」を真偽値の計算(プログラミング)で確かめる