論証の精神を2000年前から学ぶ「ユークリッド原論を読み解く」レビュー

どうも、木村（@kimu3_slime）です。

「ユークリッド原論を読み解く ~数学の大ロングセラーになったわけ~」を読みました。数学の歴史を語るときに、今から約2300年前に書かれたと言われるユークリッドの「原論（Elements）」は欠かせません。（そんなに昔の本が、今に引き継がれている……そのこと自体が驚きです）

中学で図形の分野として教えられる内容（平面幾何学）、そのほとんどが、原論を下敷きにしているのですから、驚きます。

今回は、逆に中学で教えられる数学ではわからない、原論を読むことでしか得られない内容について紹介します。

定義、公理にもとづいた論証の精神

中学の図形の分野というものは、相似や合同の概念を使って、ひたすら未知の辺の長さや角度を求めていた印象があります。僕が真面目に勉強していなかったからかもしれませんが。途中に証明問題なるものが入ってきて、「角ABC」と穴埋めする。

原論は確かに図形（幾何学）を扱います。しかし、その方法が極めて特徴的だと思います。

「ユークリッド原論を読み解く」は、命題32「三角形の内角の和は180度である」を詳しく解説しています。

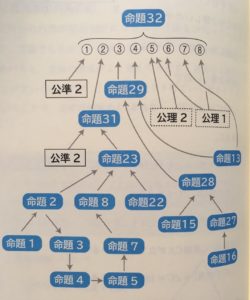
画像引用：ユークリッド原論を読み解く

命題32の証明には、じつは数多くの事実を利用しているのです。

命題31「与えられた直線に並行な直線を引ける」、命題29「平行線に関して、同位角、錯覚は等しい」と。そしてそれらも、より基本的な命題から証明されていく。

こうしてさかのぼっていく先に登場するのが、公理（と公準）です。

公準2は「有限直線を延長して一直線へ延長すること」、公理2は「等しいものに等しいものが加えられれば、全体は等しい」、公理1は「同じものに等しいものはまた互いに等しい」です。

「三角形の内角の和は180度である」……という、一見当たり前に（？）成立しそうに見える内容が、なぜ成立されるのか、その理由を基本単位（公理）まで分解し、1から構築していく。

中学の数学では、1年から3年まで分割して幾何が教えられるので、こうした命題とより基本的な命題との関係が、わかりにくいのではないでしょうか。

公理と定義にもとづいた論証の精神は、特に大学数学で大事になる考え方です。内容としては中学卒業程度の知識があれば読めるので、「ユークリッド原論を読み解く」で論証の精神を感じてみるのが良いでしょう。

参考：大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう

「ユークリッド原論を読み解く」を手にとって知ったのは、原論は幾何学がメインですが、幾何のみを扱った本ではないということです。例えばユークリッドの互除法とか、素数が無限にあることの証明、円柱円錐の体積の求め方を扱っています。

円錐の体積の求め方は、角錐の体積を使って挟み込む方法、（エウドクソス）取り付くし法を使ったもので、見事な求め方でした。なめらかなで囲まれた図形の面積や体積は、後に極限・微積分の概念が発見されてから統一的に計算できるようになりました。しかもこの議論に、（現在では実数の公理のひとつとして知られる）アルキメデスの原理が既に登場しているというのが驚きです。

また、「ユークリッド原論を読み解く」は原論そのものだけでなく、「平行線の公理」を外した幾何学、すなわち非ユークリッド幾何学も紹介しています。楕円幾何、双極幾何において「三角形の内角の和が180度とならない」ことまで解説されていて、非ユークリッド幾何の一般向けの入門としても良いでしょう。

強いて本の不満を挙げるとすれば、もっと多くの原論の内容を紹介してほしかったということでしょうか。文庫本サイズで150ページなので、コンパクトにまとまっています。

より詳しく知りたければ、「ユークリッド原論」か「ユークリッド『原論』とは何か」を読むと良いのでしょう。逆に、重い本を手にとって読まないよりは、軽い本でも読んで生かした方が良いと思うので、気軽に「ユークリッド原論を読み解く」をチェックしてみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。