どうも、木村(@kimu3_slime)です。
ゲーデルの不完全性定理についてきちんと解説できるようになりたいので、その前提となる数理論理学を少しずつ勉強しています。
今回は、数学における証明とはそもそも何なのか、健全性、完全性という性質について紹介します。
数理論理学の知識を前提とせず、やさしめに要約するつもりです。
(嘉田さんの数理論理学の講義ノートを参考にしています)
証明できる=正しい?
数学は、与えられた命題が数学的に正しいかどうか判断するという意味で、推論の学問と言えます。
推論の手段は、論理を使った証明です。数学的事実の正しさは、証明によって保証されています。
通常の数学における証明とは、どのようなものでしょうか。
例えば「AならばC」といった命題を証明したい。
証明する。前提Aが成り立っているので、Bが示せる。(略)……よって、Cが示せた。
仮定から出発して、間違った議論をせずに正しく推論して、結論が導けるとき。これが(素朴な意味で)証明できる、ということですよね。このことを、構文論(syntax)的に証明できる、と言います。
そして証明ができるときには、当然、その結果は正しいと考えますよね。つまり、命題の仮定が満たされているならば、結果は意味論(semantic)的に成り立っている。
構文論的に証明できることと、意味論的に正しいことは、実は別物です。
- 構文論的に証明できる命題は、意味論的に成り立つ
- 意味論的に成り立つ命題は、構文論的に証明できる
前者を論理体系の健全性(soundness)、後者を論理体系の完全性(completeness)と言います。
健全性は、構文論的な証明によって間違った結論が導かれないというもので、当然持っていてほしい性質です。健全性がなければ、もはや形式的な推論が機能しません。
一方で、完全性は明らかな性質ではありません。
正しい命題は常に証明できてほしいものです。しかし、その保証はどこにあるのでしょうか? 「正しい命題ならば証明できる」これは証明できるのでしょうか?
このように、ある命題が「証明できる」ことと「正しい」ことを別々に定義するのが、数理論理学の出発点と言えます。
そうすれば、どんな論理体系が、健全性、完全性といった性質を持つ(またはもたない)のか、定理として示すことができます。
一階述語論理の健全性と完全性
健全性や完全性といった性質は、考えている論理体系によって変わります。
一階述語論理と自然演繹という論理体系を考えるとき、次の健全性定理と完全性定理が成立します。
健全性定理
(記号や用語はわからないと思いますが、後に簡単に解説します)
定理5.2.
言語\(\mathcal{L}\)の閉論理式の集合\(\Gamma\)(有限でも無限でもよい)と、言語\(\mathcal{L}\)の閉論理式\(\varphi\)について、\(\Gamma \vdash \varphi \)ならば、次のことが成り立つ。
言語\(\mathcal{L}\)のストラクチャー\(\mathcal{M}\)について、\(\mathcal{M} \Vdash \Gamma\)ならば\(\mathcal{M}\Vdash \varphi\)である。
引用:数理論理学 講義ノート(2013年度版) p.26
\(\Gamma \vdash \varphi \)とは、\(\Gamma\)から\(\varphi\)が導出できること。つまり、\(\Gamma\)を公理系とする数学理論で命題\(\varphi\)が証明できると解釈できます。
\(\mathcal{M} \Vdash \Gamma\)(\(\mathcal{M}\)が\(\Gamma\)のモデルである)とは、\(\Gamma\)に属するすべての閉論理式\(\varphi\)の真偽値が\(\top\)であること。つまり、\(\Gamma\)は\(\mathcal{M}\)における公理系。
つまり定理は、どのような数学的構造\(\mathcal{M}\)、その公理系\(\Gamma\)を考えても、\(\Gamma\)から\(\varphi\)が証明できるならば、その命題は\(\mathcal{M}\)において正しいと言っています。
これは健全性そのものですね。
完全性定理
健全性は当然持っていてほしい性質でしたが、完全性はそう期待できるものではありません。
数学者のヒルベルトは、ヒルベルト・プログラムと呼ばれる計画を示し、数学体系の完全性と無矛盾性を証明しようとしました。
その一部、一階述語論理における完全性定理は、クルト・ゲーデルによって肯定的に示されたのです。
定理6.1.(自然演繹の完全性定理)
言語\(\mathcal{L}\)の閉論理式の集合\(\Gamma\)と閉論理式\(\varphi\)について、次のことが成り立つとする。
言語\(\mathcal{L}\)のストラクチャー\(\mathcal{M}\)について、\(\mathcal{M} \Vdash \Gamma\)ならば\(\mathcal{M}\Vdash \varphi\)である。
このとき、\(\Gamma \vdash \varphi\)である。(すなわち、解消されていない仮定がすべて\(\Gamma\)に属して結論が\(\varphi\)である導出図が存在する)。
引用:数理論理学 講義ノート(2013年度版) p.29
これはさきほどの逆を言っています。
\(\mathcal{M}\)を任意の数学的構造、\(\Gamma\)をその公理系とし、その論理式\(\varphi\)が\(\mathcal{M}\)において正しいと仮定する。このとき、\(\varphi\)は\(\Gamma\)から証明できる。
正しいならば、証明できる。これが完全性です。
そして、一階述語論理ではこの完全性が保証される、十分な証明能力があることが示されているわけです。これは大事な結果ですね。
ちなみに、論理体系の完全性と、ゲーデルの不完全性定理の不完全性は異なる意味です。
後者は、形式理論が不完全であることを指していて、その理論では証明も反証もできない論理式が存在することを意味します。(こちらは、不完全性というよりは、非決定性といった方が意味的に混同しにくいのではないかと思っています。)
用語、考え方の簡単な解説
健全性定理、完全性定理に関する用語と考え方を簡単に紹介して終わりたいと思います。
論理式、項、言語、一階述語論理
「証明」を数学的に扱うためには、証明するべき命題、すなわち論理式とは何か、定義する必要があります。
論理式(formula)は、「項(term)」という語によって作られた文章です。
例えば、\(x_0 < 3\)は論理式です。この論理式は、\(x_0\),\(3\)という項を、関係\(<\)で結びつけることによって作られています。
項は、例えば次のようなものひとつです。定数記号\(0,1,2,\dots\)、変数記号\(x_0,x_1,\dots\)。これらを関数記号\(+,\times\)で結びつけたものも項。
論理式は、項の組み合わせによって作られます。組み合わせるときに、述語記号\(=,<\)、論理記号\(\lnot, \land,\lor,\to ,\forall, \exists\)が使われます。
これらを書き表すときに使う記号(定数記号、関数記号、述語記号)を、言語(language)と呼びます。
数学の記述を、すべて意味を取り去って記号(言語)として扱い、論理式を定義しているわけです。
今回使っているような論理体系を、一階述語論理と言います。現代数学のほとんどは、一階述語論理(とその上のZFC公理系)によって解釈できることが知られています。
構文論:推論規則、導出図、証明
ある論理式から、別の論理式を導く推論規則も定義します。
これは、導出図(証明図)と呼ばれる図で表されるものです。
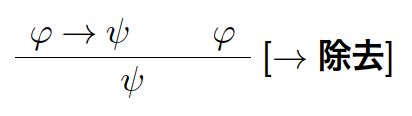
画像引用:数理論理学 講義ノート(2013年度版) p.12
真ん中に横線があり、線の上側が仮定、下側が結論です。
上の図では、\(\varphi \to \psi\)と\(\varphi\)という仮定から、\(\psi\)という結論を導いています。この推論規則を、\(\to\)除去と呼びます。
このように、論理記号を除去、導入する推論規則を定めたものが自然演繹です。
論理式\(\varphi\)が論理式の集合\(\Gamma\)から「証明できる」ことを、\(\Gamma \vdash \varphi\)と書き、次のように定義されます。
解消されていない仮定がすべて\(\Gamma\)に属し、結論が\(\varphi\)である導出図が存在する、と。
意味論:ストラクチャー、真理値
「\(1<x<2\)を満たす\(x\)は存在しない」という文章は、正しいでしょうか、間違っているでしょうか?
それは、議論している舞台となる集合によります。自然数ならば正しいですし、実数なら正しくない。また、\(<\)は単に記号だったので、その定義を変えてしまえば、真偽は変わります。
このように、論理式の真偽を決めるためには、それを解釈するための文脈が必要です。それが数学的構造、ストラクチャーと呼ばれるものです。
言語\(\mathcal{L}\)に対応するストラクチャー\(\mathcal{M}\)は、次の組です。
- 対象領域と呼ばれる集合\(M\)
- \(\mathcal{L}\)の定数記号\(0,1,2,\dots\)に対応して、\(M\)の要素が指定されている
- \(\mathcal{L}\)の演算\(+, \times\)に対応して、\(M\)の二項演算が指定されている
- \(\mathcal{L}\)の述語記号\(<\)に対応して、\(M\)の二項関係が指定されている
適切に言語、ストラクチャーを指定すれば、群などを表現することができます。
ストラクチャーが決まれば、(閉)論理式の真偽値を定義することができます。
例えば、\(\varphi\)を\(t_1=t_2\)という論理式とします(\(t_1,t_2\)は閉項)。
このとき、\(\varphi\)のストラクチャー\(\mathcal{M}\)における真偽値\(\text{eval} _{\mathcal{M}} (\varphi)\)は、次のように定義します。
\(t_1\)に対応する\(\mathcal{M}\)の要素と\(t_2\)に対応する\(\mathcal{M}\)の要素が等しいなら\(\text{T}\)、そうでないなら\(\text{F}\)と。
他の論理式に対する真偽値も、\(\mathcal{M}\)における解釈を考えながら同様に定義していけば良いわけです。
まとめ
以上をまとめると、
- 数学の文章を論理式として形式化し、
- 証明を推論規則によって定義、
- 論理式の意味、すなわち真偽をストラクチャーに応じて定義することで、
- 健全性定理:証明できる命題は正しい
- 完全性定理:正しい命題は証明できる
- これを定理として証明できるようになった
わけです。
集合論を理解した上で、数理論理学、ゲーデルの不完全性定理の理解へ向かうときに、この文章が役立てば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。