どうも、木村(@kimu3_slime)です。
現在社会の至るところで活躍しているコンピュータが生まれるきっかけとなった理論は、チューリングやゲーデルによる研究で、それらはカントールが打ち立てた集合論にもとづいています。(狭く言えば、数理論理学や数学基礎論と呼ばれる分野)
このような数学が生まれるきっかけは何だったのでしょうか? 僕は、「論理」や「命題」といった数学を記述するためのツールであったものが、それ自身を記号として表現して、数学的分析の対象にしてしまったことが、先駆けではないかと思います。
論理を記号的に分析した数学者4人について簡単に紹介し、その歴史を辿りましょう。
論理を記号化した数学者たち
ライプニッツ
ゴットフリート・ヴィルヘルム・ライプニッツ(Gottfried Wilhelm Leibniz、1646年-1716年)は、ドイツの数学者です。
ライプニッツと言えば、ニュートンとともに微積分学の発明者のひとりという印象があります。
微積分学で言えば、関数の微分を\(\frac{dy}{dx}\)と表記するのは、ライプニッツの記法と呼ばれるもの。この記法は、特に合成関数の微分、連鎖律を計算するのに有効です。また、積の微分の計算法則は、ライプニッツ・ルールとも呼ばれています。
ライプニッツは数学者であると同時に哲学者でもありました。特徴的なのが、記号によって種々の学問を統一しようとしたことです。
命題を記号によって表現し、計算によって推論の正しさを証明しようとする試みを行っています。この先駆的な業績から、記号論理学の父と呼ばれることがあるようです。
また、正しい命題を導く性質を持った形式言語、一般言語(lingua generalis)を生み出した。これは2進法による計算の発明でもあります。
2進法計算はコンピュータ計算の原理につながるものですし、形式言語は、チョムスキーの普遍文法を代表とする理論言語学、コンピュータによる言語処理につながるものです。
参考:ライプニッツの論理計算について –
竹田 浩一、 Gottfried Leibniz – history-computer.com
ド・モルガン
オーガスタス・ド・モルガン(Augustus de Morgan, 1806年 – 1871年)はイギリスの数学者、論理学者です。
高校の集合と論理の時間で学ぶ、ド・モルガンの法則
\[ \begin{aligned}\lnot (P\land Q)=\lnot P \lor \lnot Q,\lnot(P\lor Q) = \lnot P \land \lnot Q\end{aligned} \]
\[ \begin{aligned}(A\cap B)^c=A^c \cup B^c,(A\cup B)^c = A^c \cap B^c\end{aligned} \]
を定式化した人として有名ですね。
これは1847年、本「Formal logic, or the calculus of inference (形式論理学,あるいは推論の計算)」で発表されたもので、今に名を残しています。
また、数学的帰納法(mathematical induction)を現代で知られるような形で整理したことでも知られているそうです。これは調べるまで知りませんでした。
ブール
ジョージ・ブール(George Boole, 1815年 – 1864年)は、イギリスの数学者、哲学者、論理学者です。
ブールはブール代数(Boolean algebra)と呼ばれる2値真偽値のなす代数構造の発見で有名。
典型例としては、集合\({0,1}\)に2を法とする算術\( 1 + 1 = 0\)を入れると、数の和と積が真偽値のXORとANDに対応する、といったもの。
真偽値(truth values)という、命題の真偽に関する演繹を計算に落とし込むアイデアもブールによるものですね。
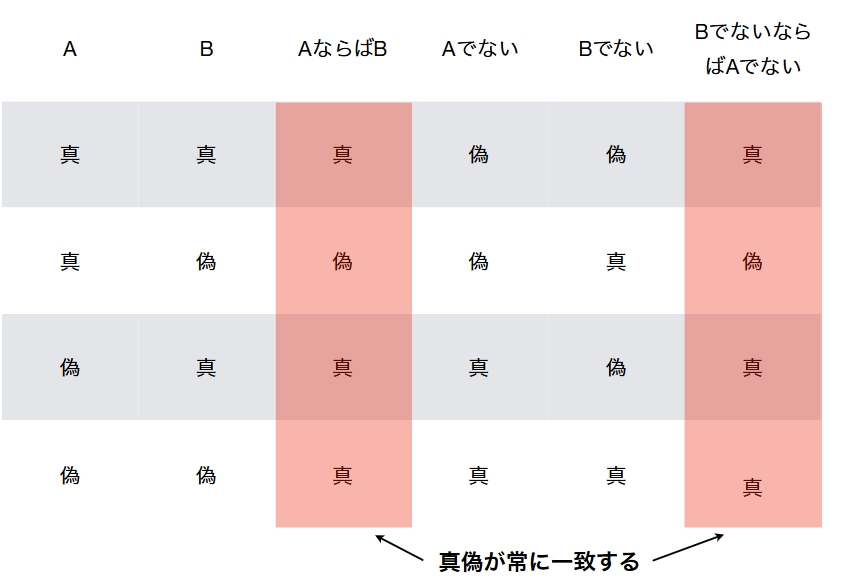
参考:「AならばB」のよくある誤解から学ぶ、論理学入門(対偶、逆、否定、真偽表)
ブール代数は、情報の理論を築いたシャノン(Shannon)などにより、のちにコンピュータへの応用が発見されました。電気回路を使って論理演算を表現する、論理回路の基礎となっています。
ブールは「思考の法則の研究」という本を著しましたが、その解説論文にかかれていた内容が面白かったです。
ジョージ・ブールによるば,実際の人間社会における,微妙なニュアンスの差というものを思い切って切り捨ててこそ,厳密な論理が成立するというのである.数学では第一に尊重される厳密性ということは,実際のライフの(*)という一次近似の上のことである.人生をラフに見ることによって,ストリィクトな論理が成立していることだというの は,現在,きわめて重要な意味をもっていると思う.
引用:思考の法則の研究 : ジョージ・ブールの生涯(応用数理の遊歩道(11))
– 山口 昌哉
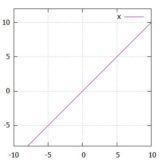
ここで(*)とは、\(x\)という記号で青いもののクラスを表すとき、青い青いクラス\(x^2\)が青いクラスと等しくなる方程式\(x^2=x\)のこと。
例えば青い青い海と青い海は、確かに違うものだが、それは二次的な違いに過ぎないとブールは言います。一次近似としては、方程式\(x^2=x\)が正しく、それが論理の世界であると。
そしてもし方程式\(x^2=x\)を成立するような\(x\)を数として考えると、\(x=0,1\)が導かれます。2値が出てくる理由が方程式として表されるのは、興味深いですね。
フレーゲ
フリードリヒ・ルートヴィヒ・ゴットロープ・フレーゲ(1848年 – 1925年)は、ドイツの哲学者、数学者、論理学者です。
彼は1879年に「概念記法」を出版しました。現在の数学でも、全称記号や存在記号\(\forall,\exists\)といった量化(quantification)は、フレーゲによるものです。また、量化を含む論理式、述語論理の生みの親とも言われています。
概念記法の副題は、算術の式言語に倣った純粋な思考のための式言語。思考のために役立つ言語、推論を、公理的なアプローチで作ろうというアイデアは、ライプニッツに通じるものがあります。しかし異なる点は、それを算術的なものにするのではなく、より広く適応される論理学を生み出そうとしたことにあります。
のちに「ブールの論理計算と概念記法」という文章を書いたように、ブールとつながりがあります。また、フレーゲは後に、ペアノの公理(自然数の公理)のペアノ、ラッセルのパラドックスのラッセルに影響を与えたと言われています。
彼の述語論理の考え方は、ラッセル-ホワイトヘッドの「プリンキピア・マテマティカ(数学原理)」へとつながり、数学の基礎となる「証明」の数学が生まれていくことになりました(数学基礎論)。
参考:『概念記法』の式言語とはどんな言語なのか – 飯田 隆、日本大学
「計算機科学や集合論は、論理を記号化するというアイデアによるものが大きい。それはカントール以前からある……誰が作ってきたのだろう?」
そんな疑問が気になって調べてみた結果、ライプニッツ、ド・モルガン、ブール、フレーゲにたどり着きました。
ド・モルガンは教科書的に有名ですが、ライプニッツやブール、フレーゲの貢献の大きさは今回初めて知りました。特にライプニッツは、数学に限らず、人間の思考活動を記号化せんとすもので、計算機科学につながりうるアイデアが17世紀時点で既にあったのが驚きです。
最近、学生時代には学ばなかった計算機科学(と数学のつながり)が気になっているので、引き続き勉強していきたいと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
現代数学社
売り上げランキング: 376,810
青土社
売り上げランキング: 63,183
日本評論社
売り上げランキング: 868,255