どうも、木村(@kimu3_slime)です。
大学数学で最初に学ぶことの多い線形代数学では、高校数学で習う「ベクトル」の知識が必要です。
今回はベクトルについて、高校数学レベルでわかりやすく解説していきます。
ベクトルがわかりにくい理由:有向線分
ベクトルとは何でしょうか?
よく「ベクトルは、大きさと向きを持つ量である」と説明されます。
点\(A(1,2)\)から点\(B(3,3)\)へ向かうベクトル\(\overrightarrow{AB}\)は、次の図のように示される矢印です。
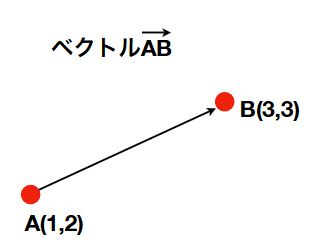
そして、2つの矢印の向きと大きさが等しいとき、それらのベクトルは等しいと考えます。
ベクトルとは矢印である。ちゃんと言うならば、有向線分である。僕にはこの考え方がわかりにくかったです。
有向線分としてベクトルを考えるのは間違ってはいません。
しかし、その考え方は大学数学で習う線形代数学であまり使いません。現状の高校数学のカリキュラムでは、ベクトルの考え方を大学で学ぶ学問へ応用するのが難しいのではないかと思っています。
高校数学のベクトル(の一部分)は、主に平面幾何の問題を解くために導入されています。そのために、「内分点・外分点の公式が~」という話が続きます。そこでの式や計算の複雑さもまた、ベクトル嫌いを生み出す原因だと思います。
(もちろん、次に紹介する座標を使ったベクトルの考え方も高校数学の範囲に入っています。両方の考え方が入っているので、高校生の当時僕は混乱していました。)
(僕は中学校、高校での幾何学での覚えるべき公式の多さにより、数学嫌いが生み出されているのではないかと懸念しています。わかりやすくて面白く応用しやすい数学が広まってほしいものです笑)
座標を導入した「位置ベクトル」はわかりやすい
では、わかりやすい考え方を紹介します。
ベクトルの定義
ベクトルとは、いくつかの数字の組のことです。(平面上の)ベクトルとは、2つの数字の組です。ここからはそう約束(定義)します。
例えば、\(a=(1,2)\)はベクトルです。これを図示してみましょう。
頭の中に、方眼紙のようなマス目が書かれた平面をイメージしてください。ベクトル\(a=(1,2)\)は、右に1マス、上に2マス進んだところにある点を指しています。
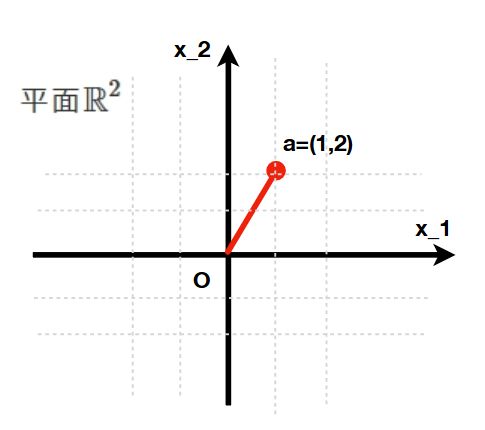
この平面は、高校数学では座標平面と呼ばれるもの。横軸が\(x\)、縦軸が\(y\)で表記されることが多いですが、ここでは\(x_1,x_2\)と書いています。
ベクトル\(a=(1,2)\)の中に書いてある数字を成分と呼びます。最初の数字は第一成分、続く数字は第二成分です。つまり、ベクトル\(a\)の第一成分は1、第二成分は2ですね。
ベクトルはいくつかの数字の組だと言いましたが、並んでいる数字の順番を入れ替えてしまうと別のベクトルになります。つまり、\((1,2)\)と\((2,1)\)は別のベクトルです。図示してみればわかりますね。
(このような順番に意味のある組を、大学数学では順序組 orderd pairと呼びます)
じつは、ベクトル\(a=(1,2)\)は矢印(有向線分)として見ることができます。つまり、原点\(O\)から座標\((1,2)\)へ向けた矢印と考えば、高校数学風のベクトルの考え方と同じです。つまり、\(a=\overrightarrow{OA}\)と見ています。
ベクトルの和:数字の足し算が、矢印の合成になる
2つのベクトルの足し算は、次のような約束です。
\(a=(a_1,a_2)\)と\(b=(b_1,b_2)\)の和は、それぞれの成分を足し合わせます。
\(a+b:=(a_1+b_1,a_2+b_2)\)
\(a=(1,2)\)と\(b=(3,-1)\)のとき計算してみると、\(a+b=(4,1)\)です。これをさきほどの平面に図示してみましょう。
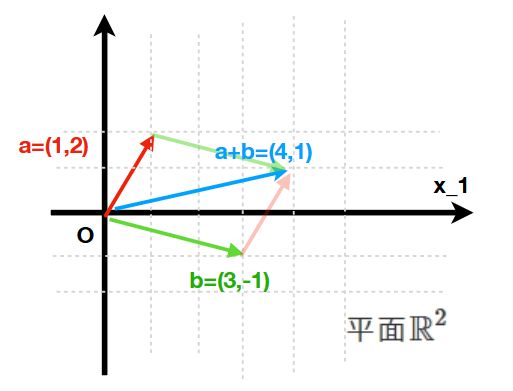
やっていたことは、各成分の数字の足し合わせです。それが確かに、赤の矢印と緑の矢印を合わせてできる青の矢印を得る操作になっていることがわかります。
このように、矢印の合成という幾何学的な操作を、成分の足し合わせという代数的な計算に落とし込めることが、ベクトルという考え方のメリットです。(もっと言えば、線形代数学のメリットのひとつ)
ベクトルを使って何をする?
ベクトルを、大きさと向きを持った線分(有向線分)ではなく、順番を持った数の組(位置ベクトル)として考える方法を紹介してきました。
これにより、ベクトルの表記は簡単になったと思います。
高校数学では、点は\(A(1,2)\)、ベクトルは\(\overrightarrow{AB}\)と言ったように表記されていました。
大学数学では、ベクトルは\(a=(1,2)\)と表記します。点は大文字ではなく小文字に、点を表す記号\(a\)とその内容\((1,2)\)を別々に。記号の数が減り、計算の方法も明快です。
ポイントは、マス目=座標を導入したことです。これにより、図的の問題=幾何的問題に、代数的方法=成分計算でアプローチできます。
(座標の考え方は、ルネ・デカルトによって始まったと言われています。そのためこの座標はデカルト座標と呼ばれます。座標を使った幾何学は、解析幾何学、あるいはデカルト幾何学Cartesian geometryとも呼ばれます。)
大学の数学・線形代数学では、ベクトルの考え方を、幾何学の問題はもちろん、それ以外にも活用します。
- 「行列」を使って、ベクトルを回転・拡大縮小・平行移動したりする(変換)
- 連立一次方程式の解をベクトルと見て、解く
- 実数だけでなく、複素数や数列、関数をベクトルとして見て分析する(線形空間)
ベクトルの考え方は、線形代数学以外にも、複素数や複素平面を扱った複素解析で役に立ちます。それぞれのトピックについて、後に記事を書く予定です。
この記事では線形代数学の前提となるベクトルの考え方を紹介してきました。この記事が読めたなら、大学数学・線形代数学の本にチャレンジできると思います。
木村すらいむ(@kimu3_slime)でした。ではでは。