どうも、木村(@kimu3_slime)です。
大学1年で教えられることの多い教養数学では、線形代数学を学びます。
行列計算を教えられることが多いですが、なぜそもそも行列の理論を考えるのか。
今回は、Googleのページランクの考え方に、線形代数学の考え方、特に固有値・固有ベクトルが使われていることを簡単に紹介します。
ページランクとは
現在でこそ「検索エンジンと言えばGoogle」「ググる=Google検索する」が定着していますが、1990-2000年代はさまざまな検索エンジンがありました。
つまり、Googleは検索精度において、他の検索エンジンよりすぐれていたから、現在ここまでの評価を得ているわけです。どうすぐれていたのか。
検索エンジンは、ウェブサイトを巡回(クロール)して情報を集め、検索する「キーワード(クエリ)」に答えてくれそうな結果を返すものです。
簡単な検索エンジンでは、「ページにキーワードがどれだけ登場するか」(など)の情報で測っていました。これだとあまり関連のないページも検索結果に出てきますし、また意図的にキーワードを入れ込むスパムも通用してしまいます。
この状況を一変させたのが、Googleのページランクという考え方です。
Googleの検索結果は、ランキング方式で表示されていますよね。あのランキングの順序をつけるために、ページの重要度・関連度を数値化するわけです。
ページランクの考え方では、ページ同士の「リンク」に注目します。「他ページからリンクがある=言及されている=価値がある」と推測できるわけです。
ポイントは、リンク数が多ければ多いほど高くなる。さらに、雑多なページからのリンクよりも、「良いページ」からのリンクの方がより価値があると考えられるので、それに応じてポイントを加算する。こうしたルールで考えます。
ページランクの考え方は、Google創業者のラリー・ペイジとセルゲイ・ブリンによって、1998年に発明されました。ふたりとも大学時代の専門は計算機科学でした。線形代数学を学ぶことは、Googleのような世界的な企業を立ち上げることに役立つかもしれません。
ページランクのみで検索結果を表示しているわけではありませんが、現在でもその評価基準は内部で使われています。
参考:Google’s Gary Illyes: Yes, PageRank Still Matters – search engine roundtable
ページランクを計算してみよう
簡単な例で、ページランク(的なもの)を計算してみましょう。
次の画像のように5つのウェブページがあって、その間にいくつかのリンクがあるとします。
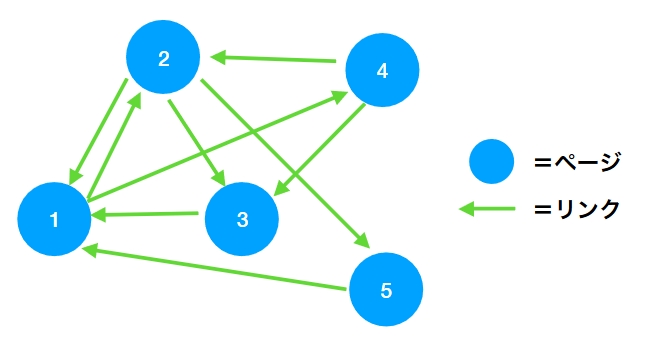
\(i\)でページの番号を表すことにします。
ページ\(i\)へのリンクよって与えられるポイント\(p_i\)を、次のように定義しましょう。
\[ \begin{aligned}p_i = \sum_{j = iへのリンクがある番号} \frac{p_j}{ページjが出しているリンク数}\end{aligned} \]
\(\sum\)は、\(j\)が満たす条件すべてにわたって、右側の数値を足し合わせることを意味しています。
例えば、\(i=1\)のときに式を書くと、ページ1は2、3、5からリンクを受けているので、
\[ \begin{aligned}p_1 = \frac{p_2}{3}+\frac{p_3}{1} +\frac{p_5}{1}\end{aligned} \]
となります。
あるページのポイントは、ざっくり言えば、リンクを受けているページのポイントの足し合わせです。このときにただ足し合わせるわけではなく、「リンクをたくさん出しているページからのポイントは(比較的)低くなる」というように重みをつけています。
同じように\(p_2,\dots,p_5\)のポイントの定義式が書き下させます。が、合計で5本の式になるので面倒です。
そこで「行列」を使います。すると、
\[ \begin{aligned}\left( \begin{array}{c} p_1 \\ p_2 \\ p_3 \\ p_4 \\ p_5 \end{array}\right) = \begin{pmatrix} 0 & \frac{1}{3} & 1 & 0 & 1 \\ \frac{1}{2} & 0 & 0 & \frac{1}{2} & 0 \\0 & \frac{1}{3} & 0 & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{3} & 0 & 0 & 0 \end{pmatrix} \left( \begin{array}{c} p_1 \\ p_2 \\ p_3 \\ p_4 \\ p_5 \end{array}\right)\end{aligned} \]
と表せます。ポイントを\(p=(p_1,\dots,p_5)\)とベクトルでまとめて表記し、行列を\(A\)とおくと、\(p =A p\)という式になります。
線形代数学では、\(\lambda\)を数、\(A\)を行列として、\(Ap = \lambda p , p \neq 0\)という式は固有値問題と呼ばれます。そして\(\lambda\)は固有値、この式を満たす\(p\)は固有ベクトルと呼ばれます。
つまり、ページランクを求める問題は、ページランクの行列について、固有値1に対応する固有ベクトル\(p\)を求める問題ということができるのです。

実際にさきほどの行列で\(p =A p\)を解くと、固有ベクトル(のひとつ)は\(p_1=1,p_2=\frac{3}{4},p_3=p_4=\frac{1}{2},p_5=\frac{1}{4}\)となります。
つまり、\(p_1 >p_2>p_3=p_4>p_5\)となっていて、ページに順位をつけることができましたね。
ページ1がリンクが集まっているので重要そうなのはわかります。
ページ4と5を比べると、ページランク「らしい」です。どちらも1本のリンクを受けていますが、4は重要な1からのリンクを受けています。これが実際に\(p_4>p_5\)と、リンクの「質」があらわれているわけですね。
参考:線形代数とGooglePageRank – 科目「線形代数」補足資料、PageRankについて調べてみた – seri::diary
実際の行列のサイズは1兆超え?
さて、さきほどの例ではサイトが5つありました。いえ、5つしかありませんでした。
現実はGoogleは世界中のあらゆるサイトをクロールしています。サイトが増えれば増えるほど、行列\(A\)のサイズは増えて、計算が大変になるでしょう。
Googleは、2008年の時点でウェブページの総数は1兆(1,000,000,000,000)を超えたと報告しています。
参考:We knew the web was big… – Google Official Blog
「internet live stats」というサイトによると、2018年時点では19兆のサイトが存在します。
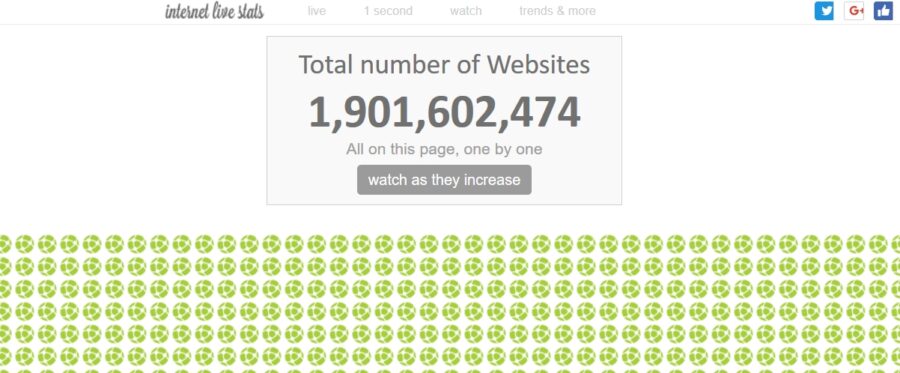
画像引用:internet live stats
このような膨大な成分を持つ計算にも、線形代数の考え方は通用します。
すべての成分が正の行列では、固有値問題が(実数として)解けるということは、ペロン=フロベニウスの定理によって保証されています。また、固有値問題をコンピュータで解くときには、べき乗法という手法が使われます。また、実際のGoogleのページランクでは、確率論の考え方(マルコフ連鎖)も用いられています。
参考:インターネットを支える数学 – 九州大学、PageRankアルゴリズムおよびそれに関連する研究について – 京都大学 総合人間学部 認知情報学系 数理情報論分野 宮嶋健人
ネットを使う人で、Google検索にお世話にならない人はいないでしょう。
ということは、同時に線形代数(や他のさまざまな数学・計算機科学)にもお世話になっている……ということが感じられたでしょうか。
線形代数の行列の理論は抽象的に感じられるかもしれませんが、Googleのページランクに使われていることを思い出せば、より現実味を感じられるのではないでしょうか。
木村すらいむ(@kimu3_slime)でした。ではでは。
共立出版
売り上げランキング: 272,186
こちらもおすすめ
なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響