どうも、木村(@kimu3_slime)です。
教養数学として学ぶ線形代数学。行列を扱う理論ですが、それがどんなふうに応用されているか、気になりませんか?
今回は、経済波及効果というものを分析するときに線形代数の考え方を使うことを紹介します。
経済波及効果とは
「風が吹けば桶屋が儲かる」ということわざがあります。
桶屋が儲かるとき、同時に銭湯屋も儲かるでしょう。また、お湯を沸かすための木材・ガスなども必要になる(売れる)でしょう。経済波及効果は、だいたいそんなものを指しています。
これはややミクロな話ですが、産業レベルで考えてみても同じ影響が起こるはずです。ノートパソコンの需要が高まったとしましょう。すると、需要を満たすため、その原料となるプラスチック、液晶、電子部品などの生産も増すでしょう。さらに、プラスチックの原料となる石油の生産も増しますね。
経済波及効果は、ある産業で起きた需要が、別の産業の生産をもたらし、次々とそれが伝わっていく現象のことです。
「波及」というのは、池に石を投げると波紋が伝わっていくように、需要が波として産業分野を超えて伝わっていくようすを表しています。
経済波及効果の分析は、実際に日本の行政(国や都道府県)においても利用されています。Google検索してみると、たくさんページが見つかります。
参考:経済波及効果とは何ですか – 埼玉県、経済波及効果分析の手引き – 滋賀県、経済波及効果推計の基礎知識 – 浜銀総合研究所
経済波及効果の求め方
産業連関表の読み方
経済波及効果を考えるときには、まず産業連関表(取引基本表、投入係数表)というデータを使います。
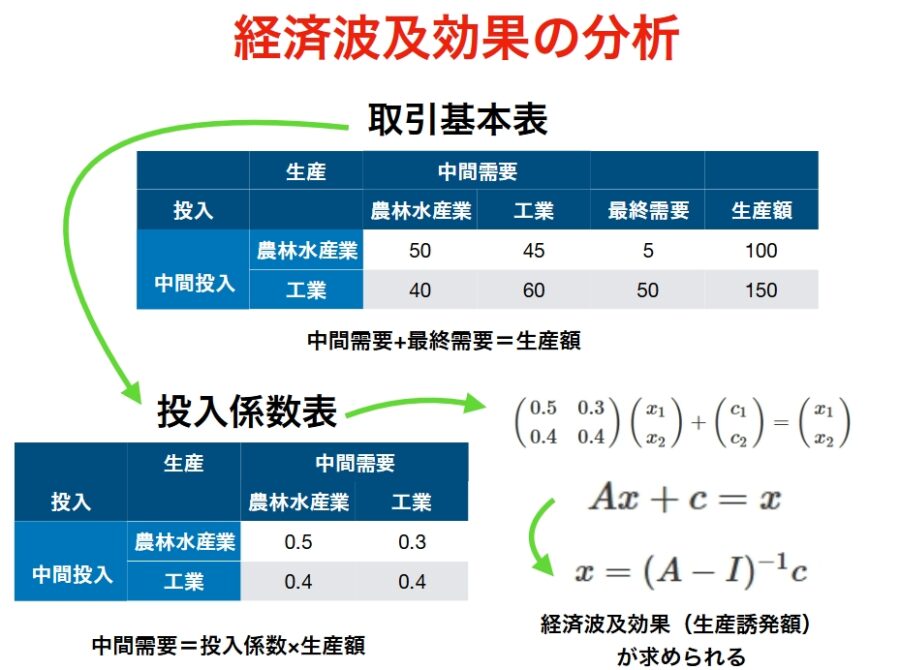
取引基本表は、一定期間(例えば1年)の間に各産業が購入した商品の額、生産した商品の額、販売した商品の額を表にしたものです。
中間需要とは、ある生産物を生み出すために必要な原材料など(中間生産物)に対する生産者の需要のこと。上の図では、工業は農林水産業から40(億)分の商品を買っています。産業間の生産のための購入額を示したものですね。
最終需要とは、市民や企業、政府による消費、投資といった需要のこと。つまり、産業の外側、一般に向けた販売額ですね。上の図では、農林水産業の最終需要は5億です。
生産額は、必ず中間需要と最終需要を足し合わせたものとなっています。
投入係数を考えよう
さて、産業連関表を使って経済波及効果を分析するにはどうしたら良いでしょうか。
新たな一般需要は、最終需要によって表されています。最終需要があったときに、どれだけの生産が生まれるか。これを予測したいわけです。
ここで、投入係数という考え方を導入します。
これは取引基本表から計算できるもので、「投入係数=生産額/中間需要」と定めます。「中間需要=投入係数×生産額」となっているので、投入係数は波及効果の強さとも言えますね。
上の図では、農林水産業は工業に対して40億分の生産をして、合計で100億生産しています。農林水産業の工業に対する生産係数は、40/100=0.4です。総生産に対してどのくらいの割合で他産業に生産しているかを示したものと言えます。
今回の分析では、投入係数は最終需要が変わっても変わらずに一定であると考えます。
取引基本表から決まる投入係数を、表にして並べてみます(これを線形代数では行列と言います)。
\( A= \begin{pmatrix} 0.5 & 0.3 \\ 0.4 & 0.4 \end{pmatrix} \)
特に今回の行列\(A\)は、投入係数行列と呼ばれます。
取引基本表では「中間需要+最終需要=生産額」という関係が成立していましたが、これに「中間需要=投入係数×生産額」を導入すれば、「投入係数×生産額+最終需要=生産額」となります。
これを数式で表すと、\( \left( \begin{array}{c} c_1 \\ c_2 \end{array}\right)\)を最終需要、総生産額を\(\left( \begin{array}{c} x_1 \\ x_2 \end{array}\right)\)として
\( \begin{pmatrix} 0.5 & 0.3 \\ 0.4 & 0.4 \end{pmatrix} \left( \begin{array}{c} x_1 \\ x_2 \end{array}\right) + \left( \begin{array}{c} c_1 \\ c_2 \end{array}\right)= \left( \begin{array}{c} x_1 \\ x_2 \end{array}\right)\)
と表せます。
より一般的に表すならば、
\(Ax + c = x\)
となります。
生産誘発額を求めよう
今回求めたいのは、新たに最終需要\(c\)があったときに、総生産額\(x\)がどれくらいになるかということです。この総生産額を生産誘発額といます。これが経済波及効果の結果ですね。
ここで線形代数学の逆行列という考え方を使います。
\(Ax + c = x\)を\(x\)について解けば
\(x = (I-A)^{-1} c\)
となります。\((I-A)^{-1}\)を行列\((I-A)\)の逆行列と言います。\(I\)は単位行列(対角成分が1、それ以外の成分は0)です。
波及効果分析においては、その成分を逆行列係数と言い、逆行列係数表と呼ばれる表を作るのが慣例となっています。
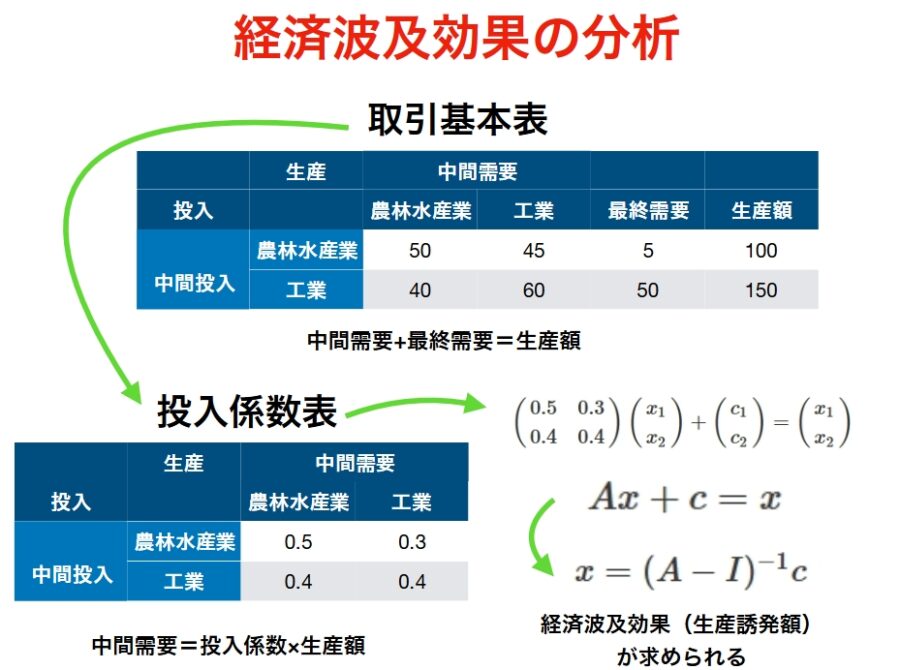
上の図の数値を使って具体的に計算してみましょう。
農林水産業に30億、工業に100億の最終需要があったとき(\(c_1 =30,c_2=100\))、生産誘発額はいくらになるでしょうか。
\((I-A)^{-1} =\frac{1}{0.18} \begin{pmatrix} 0.6 & 0.3 \\ 0.4 & 0.5 \end{pmatrix} \)なので、
\(x = (I-A)^{-1} c=\frac{1}{0.18} \begin{pmatrix} 0.6 & 0.3 \\ 0.4 & 0.5 \end{pmatrix}\left( \begin{array}{c} 30 \\ 100 \end{array}\right)= \left( \begin{array}{c} 266.6\dots \\ 344.4\dots \end{array}\right) \)
となります。農林水産業では約266億、工業では344億の生産が誘発される、ということが予測できました。
今期の産業の統計情報(取引基本表)があれば、新規需要額に応じて来期の生産額が予測できる、というわけです。
実際、国や都道府県レベルで生産誘発額が計算されています。
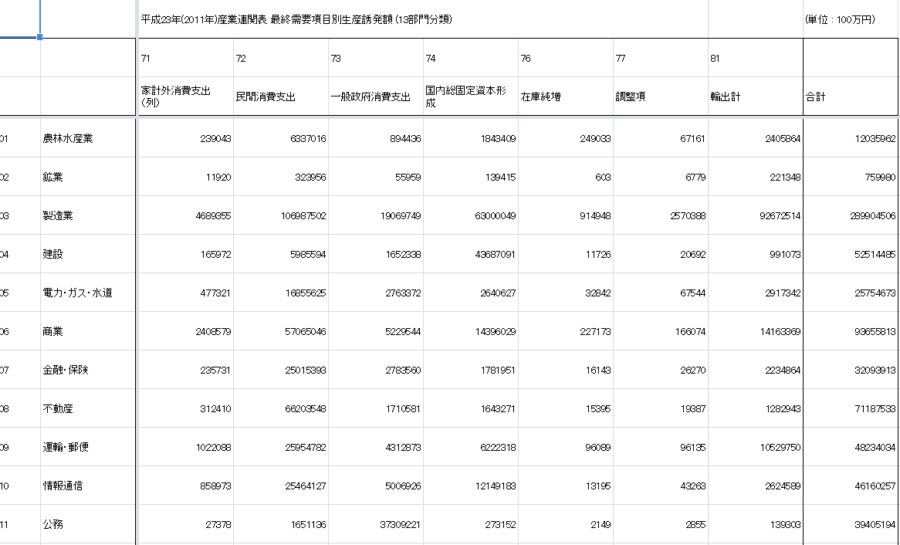
画像引用:平成23年(2011年)産業連関表 最終需要項目別生産誘発額 (13部門分類) – e-Stats
経済波及効果分析の注意点
経済波及効果の分析は、ある種の仮定のもとになりたっていて、万能のものではありません。
例えば、最終需要額がどのくらいかは、分析する人が設定するもので、それによって結果は変わります。
投入係数は年間で変わらないと仮定しましたが、生産技術が大きく発展すれば変化する可能性があります。
また、波及効果がどのくらいの期間で達成されるかは不明です。波及効果自体は存在するものの、それがどのくらいのタイムスケールで現れるかは、この分析からはわかりません。
波及効果分析、産業連関表は、ソビエト出身の経済学者レオンチェフがアメリカで開発したものです。1973年にその業績でノーベル経済学賞を得ています。
そのアイデアは、ワルラスの一般均衡理論、ケネーの経済表の考え方を合わせたことによって生まれたそうです。経済学と数学の組み合わせが、より現実的な分析の役に立ったと紹介しやすい話です。
詳しくは:産業連関表の沿革と我が国における作成状況 – 総務省
実際の行列はもっと大きい
今回は、分析の方法をわかりやすく理解するために、農林水産業と工業、2つの産業のみを考えました。そのため、行列のサイズは小さく、2行2列で表せました。
より多くの産業を考えようと思ったら、より大きな行列を考える必要があります。
例えば、次の政府の統計では、13の産業を考えているので、13行13列の行列を考える必要がでてきます。
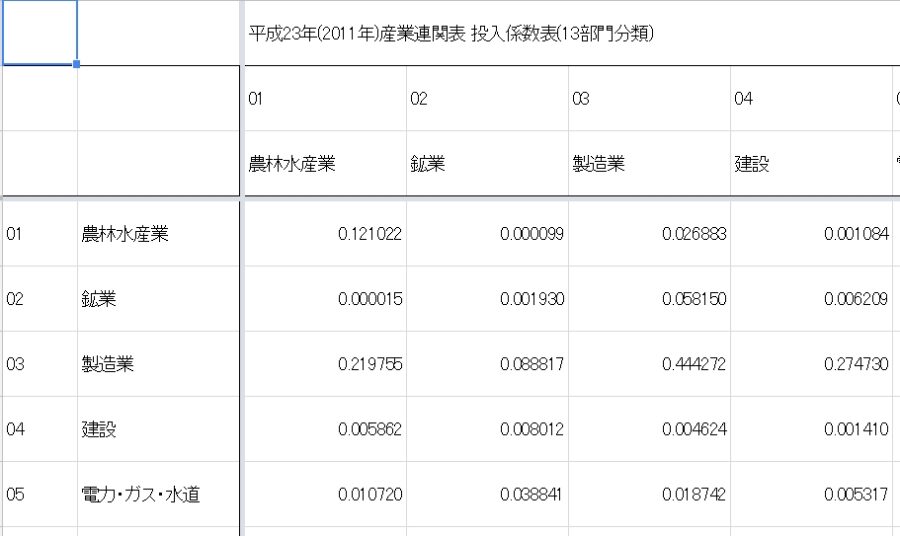
画像引用:平成23年(2011年)産業連関表 投入係数表(13部門分類) – e-Stat
産業をさらに細分して考えれば、行列のサイズはさらに大きくなるでしょう。100行、1000行、1万行……。
線形代数学では、2行2列の行列だけでなく、1億行1億列、さらには\(n\)行\(n\)列の行列、その逆行列を求める方法を学ぶことができます。
新たな需要が他の産業にどれだけ波及するかを調べる波及効果分析において、線形代数学の考え方が役に立つことが伝わりましたでしょうか。
こうした応用例を知っていれば、線形代数学で一般のサイズ\(n\)の行列の逆行列を考えるモチベーションがわかりやすいかと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響