どうも、木村(@kimu3_slime)です。
別の記事で、「集合とは、ものの集まりである」という話をして、自然数\(\mathbb{N}\)や実数\(\mathbb{R}\)など数の集合を紹介しました。
\(A=\{1,2,3\}\)といった要素が数え切れる集合のことを、有限集合(finite set)といいます。一方で、自然数\(\mathbb{N}\)の要素を数え尽くすことはできません。このように、有限集合でない集合のことを無限集合(infinite set)といいます。
数学は昔から「無限」といったものを扱ってきましたが、特に「無限集合」の性質は、馴染みがない人からすると奇妙で面白いものです。
今回は、その例としてガリレオのパラドックス、ヒルベルトの無限ホテルの無限ホテルという話を紹介します。
ガリレオのパラドックス
ユークリッドの公理のひとつに、「全体は部分より大きい」というものがあります。
これは一見当たり前に思えますよね。ケーキを切って分けたら、その一部分が全体より多くなることなんてありえません。
\(A=\{1,2,3\}\)としたとき、どのような部分集合\(B\)を考えても、その要素の個数は\(A\)を超えることはありません。
また、10以下の自然数の集合に対し、10以下の平方数(ある自然数の二乗によって表される自然数)の集合は\(\{1,4,9\}\)となり、要素の数は後者の方が少なくなります。
ところが、これを無限集合の場合で考えると事情が違うのです。
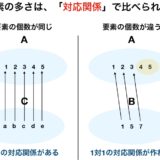
\(1 \leftrightarrow 1^2,2\leftrightarrow 2^2,3\leftrightarrow3^2, \cdots,n\leftrightarrow n^2,\cdots\)
といったように、自然数の集合\(\mathbb{N}\)と平方数の集合(\(S\)としましょう)の要素には一対一の対応関係を作ることができます。
\(S\)は\(\mathbb{N}\)の部分集合であり、5のように平方数でない数はいくらでもあります(これを真部分集合という)。
しかしながら、対応関係を見るとどちらも同じだけ個数があると言わざるを得ません。だって、もし\(S\)の方が少ないというなら、\(S\)の要素では\(\mathbb{N}\)に対応し尽くせないはずですが、上で見たようにそんなことはないのですから。
(数学の言葉を使えば、\(f(n)=n^2\)と定めれば、\(f\)は\(\mathbb{N}\)から\(S\)への一対一対応の写像となるから、という)
有限の範囲では、確かに自然数の方が平方数より多い。しかし、無限の範囲を考えれば、自然数の要素と平方数の要素はどこまでいっても対応を考えられる。つまり、「全体は部分より大きい」が正しくなくなる。
これをガリレオのパラドックスといいます。地動説を唱えたあのガリレオ・ガリレイですね。
(ちなみに、平方数全体の集合だけでなく、偶数全体の集合、奇数全体の集合、素数全体の集合などについても自然数と同様の「個数」があると言えます。考えてみてください。)
彼はこう述べています。
平方数は自然数全体と同じだけの数があると結論せざるをえない。
引用:新科学対話
だから、無限の大きさを比較するような議論は無意味だと、彼は結論しました。
無限の要素を持つ集合というものは、ユークリッドの公理に反するような状況が起こるくらい、アブナイものであったということがガリレオのパラドックスから感じ取ることができるでしょう。
(現代の数学では、無限の「大きさ」を定義した上で議論する方法が生み出されています。)
参考:数学基礎論と消えたパラドックス – Sendai Logic Homepage
ヒルベルトの無限ホテル
ヒルベルトの無限ホテルとは、無限に部屋があるホテルのことです。廊下をどれだけ歩いても、新しい部屋が登場し続けます。このようなホテルが満室のとき、新しいお客さんは入れるでしょうか?
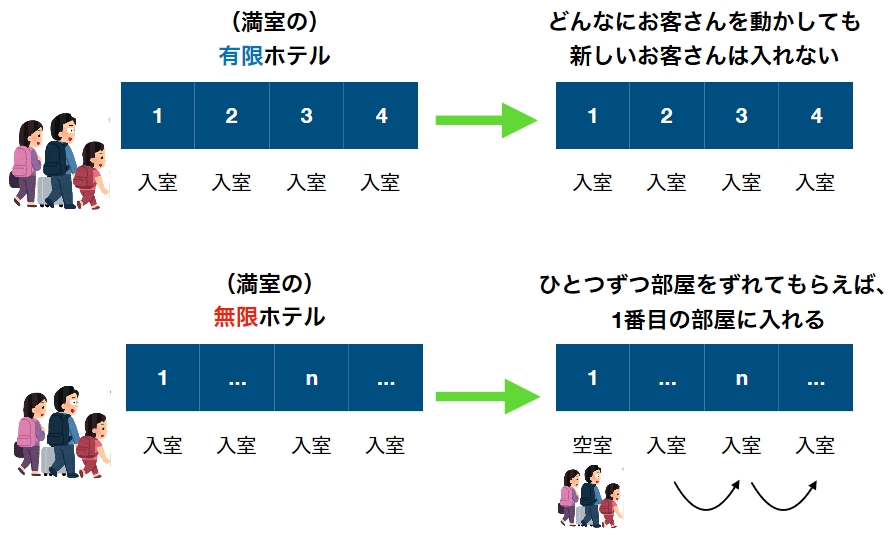
無限はわかりにくいので、有限ホテルと対比させてみます。
有限ホテルが満室のとき、入室しているお客さんをどんなに動かしても、新しいお客さんは入れません(同室させるのはナシ)。ホテルがどんなに大きかろうが、満室であれば新しいお客さんは泊まれません。これは当たり前ですね(笑)。
満室の無限ホテルはどうでしょうか。1,2,3,…と部屋に番号が振られていて、どの部屋を見てもお客さんが入っています。ここに新しいお客さんが来たときでも、このホテルには泊まることができてしまうのです。
1号室のお客さんには2号室に、2号室のお客さんには3号室に……といったように、n号室の人にはn+1号室に移ってもらえば良いのです。無限に部屋があるのですから、後ろがつっかえてしまうことがありません(有限ホテルだと、ここが無理)。
そうすると、1号室が空いていますね。ここに新しいお客さんが入れるわけです。
満室なのに泊まれてしまう。これをヒルベルトの無限ホテルのパラドックスといいます。パラドックスといっても、数学的な意味での矛盾ではなく、一見して奇妙が起こっているように見えるという話ですね。
参考:ヒルベルトの無限ホテルのパラドックス – Wikipedia
新しいお客さんが一人ではなく、複数人でも、あるいはいくらでも多くても(無限)泊まれます。n号室の人に2n号室に移ってもらえば、n人分の空室ができますよね。
またホテルを考えたのは本質的ではなく、例えば車のパーキング(無限パーキング)を考えても同じ議論ができますね。いろいろ考えてみてください。
無限集合の不思議
ガリレオのパラドックス、ヒルベルトの無限ホテルのパラドックス、どちらも有限集合を考えたときには起こりえない、無限集合を考えたときに起こる不思議な現象について紹介しました。
無限の世界では、有限の世界の常識が通じません。困ったことでもありますが、また興味深くもありませんか。
集合論では特に、無限集合の要素の「個数」を濃度と呼び、分析がなされてきました(定義は後ほど紹介します)。
自然数の集合\(\mathbb{N}\)と実数\(\mathbb{R}\)はどちらも要素を無限に持つ集合です。この無限は同じ「濃さ」を持っているでしょうか? 対応関係をつけられるでしょうか。考えてみてください。
次回は、濃度の話、カントールの対角線論法を紹介したいと思います。
関連記事:無限集合の多さ(濃度)はどのくらい? 可算無限、カントールの対角線論法とは
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店
売り上げランキング: 389,678
こちらもおすすめ
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える