どうも、木村(@kimu3_slime)です。
大学数学の基礎:集合論のはじまりの話として、集合の定義、集合論でよく使う集合や、ラッセルのパラドックスという話を紹介します。
集合の定義、要素とは
さて、集合(set)とはなんでしょうか。内田「集合・位相入門」によると
集合とは、いくつかのものをひとまとめにして考えた’ものの集まり’のことである。
です。「もの」のことを要素(element)と呼びます。
例を見てみましょう。\(A=\{1,2,3,4,5\}\)は集合です。1や2は要素です。要素をカッコ\(\{\}\)で囲むことで集合を意味するものとします。
要素が集合に属していることを、記号\(\in \)で書きます。例えば\(3\in A\)と、記号がまとまっている側に要素を、広がっている側に集合と書くことにします。含まれていない場合はスラッシュで否定を意味します、\(7\not \in A\)。
少し紛らわしいですが、一つの要素を持つ集合\(\{1\}\)とその要素\(1\)は別物です。つまり、\(1\in \{1\}\)ではありますが、\(1 \neq \{1\}\)です。
集合と要素はセットの概念です。「この要素は何の集合に属しているのだろう」「この集合の要素は何だろう」といった問いが集合を使った数学の考え方です。
集合論でよく使う集合
集合論でよく使う集合として、数の集合を紹介します。
自然数全体の集合を\(\mathbb{N}\)、整数の集合を\(\mathbb{Z}\)、有理数の集合\(\mathbb{Q}\)、実数の集合を\(\mathbb{R}\)、複素数の集合を\(\mathbb{C}\)と書く慣習があります。
記号は英語の頭文字を取ったもので、Natural number、Real number、Complex numberはわかりやすいです。整数はドイツ語で数を意味するZahlen、有理数(Rational number)は実数とかぶるので商(Quotient)から取っています。
集合には、主に2種類の表し方があります。
さきほどの集合は、\(\{1,2,3,4,5\}=\{n\in \mathbb{N}\mid 1\leq n \leq 5\}\)とも表されます。具体的に要素を書かずに、\(\{x\in X (母体となる集合)\mid x が満たす条件\} \)と条件によって集合を定める書き方です。
要素を列挙する書き方を外延的記法、条件で定義する書き方を内包的記法といいます。後者のほうがよく使われる印象です。
例えば、\(O= \{n \in \mathbb{N} \mid \exists m \in \mathbb{N} \ n=2m \}\)と定義すればこれは偶数全体の集合です。
論理記号について:集合論のはじまり、全称命題と存在命題、論理記号を知ろう
この集合\(O\)は、\(O= \{2m \mid m \in \mathbb{N} \}\)と存在記号が省略して書かれることがあります。
より一般には、\(\{x \mid \exists y \in X (x=f(y))\} \)は、\(\{f(y) \mid y \in X\} \)と略記することがある。この内包的記法の省略は、置換的記法と呼ばれます。記法の呼び方は覚える必要がなく、実際に何を含む集合なのか読み取れることが大事です。
数の集合同士にはどんな関係があるのでしょうか。例えばすべての自然数は整数であり、すべての有理数は実数です。
集合\(A\)の要素がすべて集合\(B\)に含まれることを\(A\)は\(B\)の部分集合(subset)であるといい、\(A\subset B\)と書きます。
すると、\(\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C} \)という関係にありますね。
解析学でよく使うのは、実数\(\mathbb{R}\)の部分集合です。
\( (a,b):=\{x \in \mathbb{R}\mid a < x < b\}\)を開区間\((a,b)\)、\( [a,b]:=\{x \in \mathbb{R}\mid a \leq x \leq b\}\)を閉区間\([a,b]\)と呼びます。
端っことなる点を含んでいるのが閉区間、含まずに開いているのが開区間です。
例えば\(f(x)= \frac {1}{x}\)という関数は\(x=0\)のところで考えたくないので、開区間\((0,1)\)上で考えればいいわけです。
また、2次元や3次元の空間を集合として定めることもできます。\((0,1,2)\)といったベクトルを要素として見るには、集合\(\mathbb{R}^3:= \{(x_1,x_2, x_3) \mid x_1 \in \mathbb{R},x_2 \in \mathbb{R}, x_3 \in \mathbb{R}\}\)を考えればいいわけです。
これを一般化すれば、\(\mathbb{R}^N:= \{(x_1,\cdots, x_N) \mid x_1 \in \mathbb{R},\cdots, x_N \in \mathbb{R}\}\)ですね。\(\mathbb{R}^N\)という集合はユークリッド空間と呼ばれます。
1次元のユークリッド空間\(\mathbb{R}\)は数直線、2次元のユークリッド空間\(\mathbb{R}^2\)は平面、3次元のユークリッド空間\(\mathbb{R}^3\)は空間として幾何学的に見ることもできますね。
参考:集合、構造、空間とは何か? ユークリッド空間\(\mathbb{R}^N\)を例に考える
また、平面\(\mathbb{R}^2\)において、\(x_1 ^2 +x_2 ^2 =1\)を満たす点\((x_1,x_2)\)は円周です。これを\(S^1 = \{(x_1,x_2)\in \mathbb{R}^2\mid x_1 ^2 +x_2 ^2 =1\}\)と書けば円周の集合ですね。
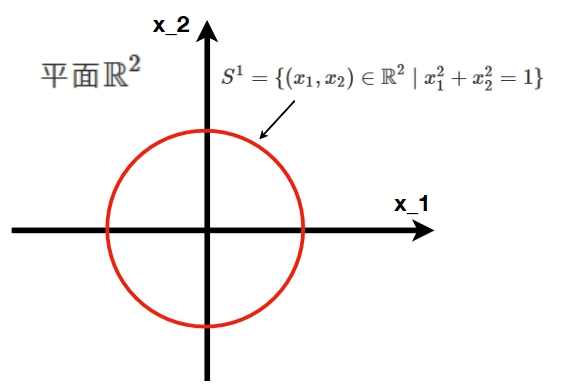
一般化して\(S^{N-1} = \{(x_1,\cdots,x_N)\in \mathbb{R}^N\mid x_1 ^2 +\cdots + x_N ^2 =1\}\)を球面(sphere)の集合と言います。
このように、\(\mathbb{N}\)や\(\mathbb{R}\)といった数の集合や、その部分集合を考えることで、さまざまな集合を舞台として設定できますね。
ラッセルのパラドックスとは
数学では、数の集合以外にも、関数の集合や数列の集合、行列の集合など、さまざまな集合を考えます。
「集合とはもの(要素)の集まりである」というのが集合の定義でしたが、この定義では扱い難い対象も存在します。それを指摘するのがラッセルのパラドックス(Russell’s paradox)です。
\(X:=\{Yは集合 \mid Y\notin Y \}\)という集合を考えてみます。これは自分自身を要素として持たない集合を集めた集合です。
\(X \in X\)と\(X \notin X\)、どちらが成立するでしょうか。
仮に、\(X \in X\)であったとしましょう。このとき、\(X\)の定義から\(X \notin X\)です。つまり仮定は正しくありません。
また仮に、\(X \notin X\)であったとしましょう。\(X\)の定義(の否定)から、\(X \in X\)が成立します。この仮定も正しくありません。
つまり、\(X \in X\)と\(X \notin X\)のいずれも成立しないので(排中律に反する)、これは矛盾と言えます。
矛盾を導く過程に間違いはありません。つまり、前提に問題があるわけですね。「集合の集合」といったものを集合として扱ったのが問題でした(さきほどの\(X\)は集合として存在しない)。
このような\(X\)が集合として存在する、ということを認めてはいけなかったのです。集合とは何かを制限をかけて定義する方法は、公理的集合論(axiomatic set theory)と呼ばれます。
特に現在では、ツェルメロ-フレンケル(Zermelo–Fraenkel)の公理系(ZF)に選択公理(C)を加えた公理系、ZFC公理系が主流の集合論体系として使われています。
一方で、「集合とはものの集まりである」と素朴に定義して議論に差し支えない分野は多いです。じっさい、数学科における2年次集合と位相の講義でZFC公理系にもとづいた集合論に踏み込むことは少ないかと思います。そのような立場は、素朴集合論と呼ばれます。
参考:Is “naive set theory” really naive? – 数理解析研究所講究録
僕は、初めて集合論を学ぶならば、まずは\(\mathbb{N}\)や\(\mathbb{R}\)といった数の集合、その部分集合を具体例として学んでいけば良いかと思っています。
集合論の基礎について知りたいならば、公理的集合論、ZFC公理系、数理論理学といったキーワードで調べてみると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える