どうも、木村(@kimu3_slime)です。
僕たちの住む地球は、太陽系の中で太陽を中心として動き続けています。
太陽系の惑星はずっとこのまま安定に動き続けるのか? 惑星と惑星がぶつかったり、どこか遠くへ飛んでいってしまうことはないのか?
という「太陽系の安定性」の話は、天体力学を築いたラプラス(1749-1827)やラグランジュ(1736-1813)の頃から、大きな問題とされてきました。
複数の惑星の運動は、物理的には多体問題(N-body problem)として定式化されます。複数の物体が、それぞれの間で万有引力を受けて動いているというモデルです。
例えば、太陽と地球のみを考慮した2体問題は、ニュートンによって解かれています。(参考:The Two-body problem – 北海道大学)
では、もう一つの惑星との運動を考えた、3体問題はどうなのか。じつは、ポアンカレ(1854-1912)によって、一般の3体問題の解は積分法によって求められない、つまり「解けない」ことが証明されています。
「解けない」とは
「解けない」とは、3体問題の解が存在しない、ということではありません。3体問題の数式によって決まる運動は確かにある。
しかしそれは複雑過ぎて、一般には積分法によって求めることができない、という話です。
もう少し述べると、ポアンカレは「Les méthodes nouvelles de la mécanique céleste」において、「(近可積分系は摂動パラメータについて)解析的な第一積分を持たない」ことをを示しています。
参考:近可積分系の諸問題をめぐって 安定性の視点から – 数理解析研究所講究録
第一積分は、保存量とも呼ばれるもので、それがあると方程式の変数を減らして解くことができます。3体問題ではそれをどうやっても見つけられないので、解けない、というわけです。
注意したいのは、3体問題が全く解けないわけではない、ということです。特殊なケースでの解はいくつか示されています。
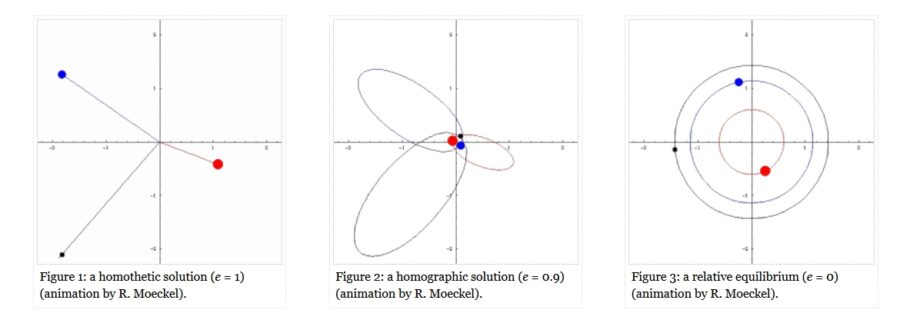
画像引用:Three body problem – scholarpedia
特に、ラグランジュ解(正三角形解)と呼ばれる解は美しいです。太陽・木星・トロヤ群の小惑星は、実際にこのラグランジュ解を作っていると言われています。(参考:シミュレーション天文学 – 神戸大学)
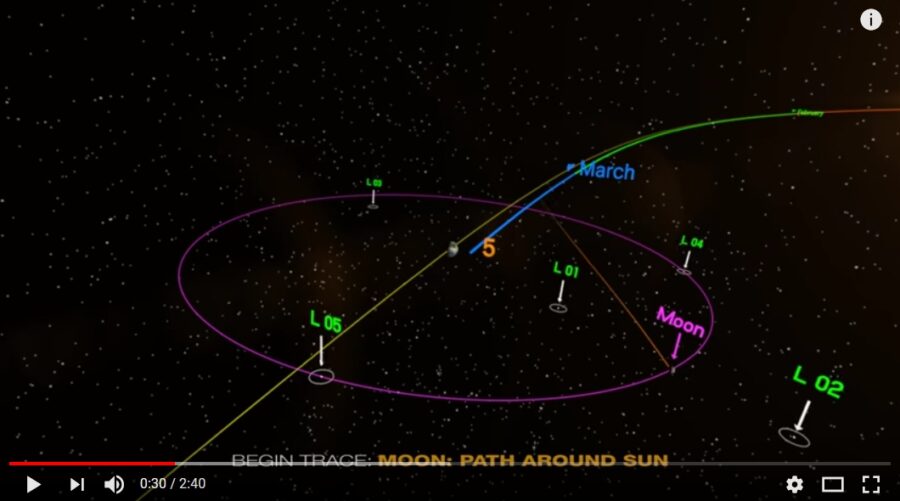
画像引用:lagrange points animation
ちなみに、シミュレーションによると、太陽系の惑星の運動は安定ではない(不安定)という結果が示されています。いつか惑星が惑星でなってしまうようなケースが訪れるのでしょうか。(参考:シミュレーション天文学 – 神戸大学)
解けない方程式を調べよう 力学系理論へ
とはいえ、ポアンカレによってわかったのは、「解ける」方程式はごくまれであり、ほとんどが「解けない」方程式であるということでした。
世界は決定論的に決まっていたとしても、それがわかりやすい数式によって表示できるとは限らないことが判明してしまったのです。
だとしたら、個別具体的なケースを調べ、近似解を数値シミュレーションによって見つけるしかないのか……。そんなことはありません。
ジョジョの奇妙な冒険では、犬におもちゃをとられたときに、『逆に考えるんだ 「あげちゃってもいいや」と考えるんだ』というセリフがあります。
微分方程式が解けない? 逆に考えるんだ 「解けなくてもいいや」と考えるんだ。
こうしてポアンカレによってはじまったのが、力学系理論(dynamical system theory)です。
力学系は、力学(mechanics)とは違います。微分方程式の解のダイナミクス、つまり「解の動きや挙動はどうなっているのか?」を考える分野です。
解を数式で表すこと(解析解を得ること)はあきらめる。
そのかわりに、解が時間が経つとどうなっていくのか(漸近挙動)や、解の安定性(初期条件がちょっと変わっても同じ結果になるか)、システムを少し変えたときに解は同じ挙動を示すのか(構造安定性)といった問題を考えよう。それが力学系理論です。
力学系理論の話は、解を数式として求めることではなく、その挙動を図示・視覚化せんとすることが多く、教科書を見ていて面白いことが多いです。
別の記事では、常微分方程式の力学系理論など、より具体的な力学系の考え方を紹介していきたいと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガーフェアラーク東京
売り上げランキング: 1,477,003
共立出版
売り上げランキング: 1,093,194
シュプリンガー・フェアラーク東京
売り上げランキング: 1,091,970