どうも、木村(@kimu3_slime)です。
豊かな国を作るためには、富・食料と人口のバランスが大事です。
ところが、そのバランスは必ず崩れてしまうのではないか。つまり、食料の生産速度に比べて、人口の増加速度は速いのではないか。
そんな問題を提示した、マルサスの法則(とその数学的な側面)について紹介したいと思います。
マルサスの法則とは
トマス・ロバート・マルサス(1766-1834)は、『人口論』を著した経済学者です。
彼は人口の増え方を考えるために、2つの仮定を置きました。
- 人口が増えるための、十分な食料(生活資源)がある
- 人間の性欲は不変であり、ほぼ必ず繁殖する
このとき、マルサスのモデルは次のような微分方程式によって表されます。人口を\(u\)として
\[ \begin{aligned}\frac{du}{dt}= u\end{aligned} \]
つまり、人口の増加率は、そのときの人口に等しいということです。人口が増えれば増えるほど、生殖可能な人口が増え、人口増加率が増すわけです。
このようなモデルを解くと、人口の時間変化は
\[ \begin{aligned}u(t)=u_0 e^t\end{aligned} \]
となります。\(u_0\)は初期人口、\(e\)はオイラー数(ネイピア数)と呼ばれる時間によらない定数です。
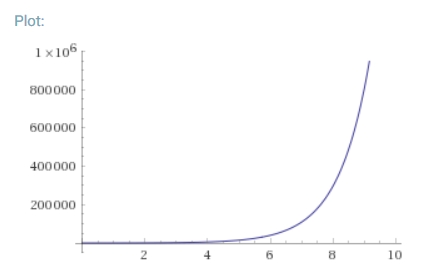
倍々ゲームのように、時間が経てば経つほど、人口が伸び上がっていく……このような増加の仕方を、指数的増大(マルサス的成長)と言います。たとえば\(t=10\)のときは最初の2万倍、\(t=100\)のときは最初の\(10^{43}\)倍も増えます!
実際マルサスは、25年間で人口が倍になったアメリカのケースを示しています。マルサスの法則に従うような成長はあるのです。
人口がこのように増えるのに比べ、食料の生産はより穏やなものでしょう。マルサスは、時間が経てば食料はその分だけ増える、つまり線形的な増加(1次関数)を想定しました。
まとめると、こうなります。人口は爆発的に増えるけれども、食料は地道にしか増えない。つまり、時間が経てば、人口>食料という関係性になり、その差はますます大きくなっていく。必然的に食糧問題や貧困が発生する……。
少し悲観的ですが、人類が必ず迎えるであろう現実を見つめようとした結果です。
人類が増えすぎて困る……ではなく、増えてしまうのだから、それを基準に貧困の問題を考えましょう、というポジティブな提案が良いですね。
少子高齢化を迎える日本では、マルサスの法則は当てはまらないでしょう。あくまで成長する国を説明した法則と言えます。
人口を数式として(時代や国によらず)普遍的に表すのは難しいです。そのため、マルサスの法則は、生物の増殖・生態学の分野において言及されることが多いです。
倍々ゲームのように増える法則は、人だけでなく、よりシンプルな生き物、バクテリアなどの微生物や細胞の増殖にもあてはまります。
その増殖には、誘導期、対数期、静止期、死滅期という4つの期間があると言われます。
そのうち対数期は、指数増殖期とも呼ばれ、微生物が指数関数的に増加し、対数関数で測らなければ増加が捉えられないくらい勢いよく増える時期を指しています。
微生物は実際に、マルサスの法則にしたがって増える時期があるわけです。
マルサスの法則は、とてもシンプルで覚えやすく、生態学の基礎となる方程式とされています。
\[ \begin{aligned}\frac{du}{dt}= u\end{aligned} \]
資源の限界によって人口増殖が止まることを示した方程式として、ロジスティック方程式が提案されていますが、これもマルサスの法則があってのものです。
人口や生物の増殖を学問的にとらえると、微分方程式が登場する……マルサスの法則は、そんなことが感じられるわかりやすい例だと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。