どうも、木村(@kimu3_slime)です。
僕が高校から大学に入学する直前に、数学の予習でもしておこうと、何もわからないまま、近所の書店で微積分学の教科書を買いました。
宮島「微分積分学」は、文章が多く丁寧なのですが、当時の僕にはわからないことだらけ。
例えば、第1章に出てくる次のような記述です。
定義
次の(1.1)、(1.2)をみたすような、実数の部分集合\(A,B\) の組\((A,B)\)を実数の切断という。
\[ \begin{aligned}A,B\neq \emptyset, A \cap B = \emptyset , A \cup B = \mathbf{R} \tag{1.1} \end{aligned} \]
\[ \begin{aligned}任意の a\in A,b \in B に対して a<b が成り立つ \tag{1.2} \end{aligned} \]
当時はこの記述に「は???」となっていた記憶があります。(今見れば、あー普通に切断じゃん、って見えますが。)
このあたりを読み飛ばしても、いわゆる「イプシロン・デルタ(\(\varepsilon-\delta\))論法」もわけがわからない。結局、高校数学以上のことは何も理解できなかったような気がします。
今回は、当時の僕のようにならないように(!)、大学数学の教科書の読み方、特に「定義・命題・証明」を紹介します。
定義・命題・証明とは
大学の教科書は、「定義!命題!証明!定義!命題!証明!」の連続です。まずこのスタイルを理解しなければ、内容に踏み込むことはできません。
定義、公理とは
定義(definition)とは、言葉の意味を限定し共有することです。
小中校までの数学では、計算が多く、あまり明示的に定義という言葉を見かけないかもしれません。あまりに当たり前の出発点とされており、定義をベースにした基本的な議論はごまかしておく傾向があるので。
例えば、次の文章は定義です。
定義(偶数)
自然数\(n\) が偶数であるとは、\(n\)が2で割り切れることである。
「同じことを繰り返していっていない?」と思うかもしれません。違います。偶数という言葉の使い方を、明示的に「約束」しているのです。
なんとなくのイメージで偶数か偶数でないかを考えることなく、何もしらない宇宙人になったつもりでも話ができるよう、定義をしています。
定義があると、それを使って話をすることができます。次のように。
「4は偶数です。」
なぜですか?
「4=2*2であり、2で割り切れるから(偶数の定義)です。」
「9は偶数ではありません。」
なぜですか?
「9=2*4+1であり、2で割り切れないから(偶数の定義)です。」
このように、定義があれば、なぜなのか理由を話すことができます。「なぜですか?」「当たり前じゃん」は、大学数学の世界ではアウトです。
「当たり前」と思えることを突き詰めるのが、大学数学の一側面です。一見すると当たり前に見えることの前提を明らかにし、直感だけで考えて間違えた議論をしないようにするために、定義は大事なのです。
定義と似た言葉に、公理(axiom)があります。スーパー基本的な定義と言えば良いでしょうか。
定義に含まれる言葉の定義は何か…とさかのぼっていけば、公理にたどり着きます。公理は前提として正しいことを認め、議論の出発点とするためのものです。
例えば偶数の定義には、自然数が前提となっています。
自然数なんて1,2,3じゃん……ではなく、定義から話をすることができるのです。自然数の基本的な定義はペアノの公理と呼ばれています。(参考:ペアノの公理 – Wikipedia)
中学校の幾何の時間で教えられるユークリッドの幾何学には、いくつかの公理(公準とも)があります。例えば、平行な2つの線は交わらないという公理(平行線公理)があります。これを議論の出発点とするわけです。
「当たり前じゃん」と思いますか? しかしこれは平面を前提とした幾何学なのです。例えば、球面では2つの平行な線が交わります(球面における直線、平行という言葉の定義は自分で調べてみてください)。平行線公理は満たされないわけです。このような幾何学を非ユークリッド幾何学と言います。(参考:非ユークリッド幾何学 – Wikipedia)
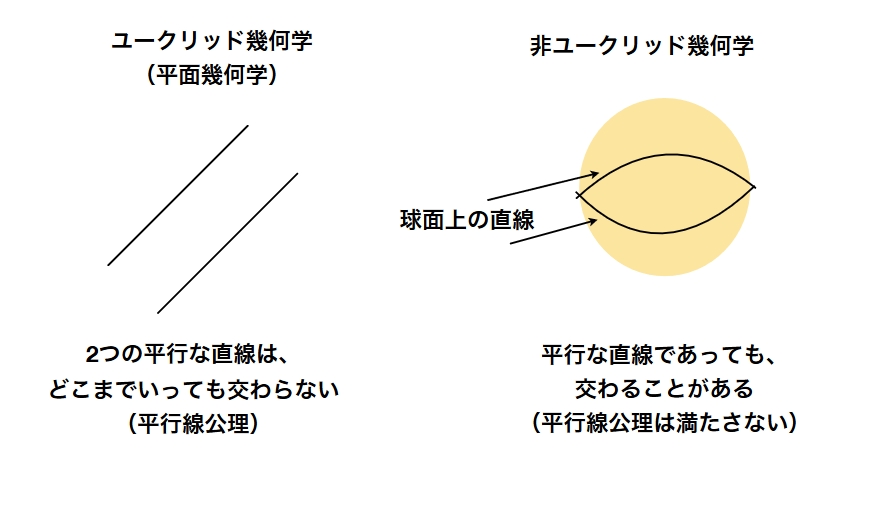
ユークリッド幾何学と非ユークリッド幾何学、どちらが正しいという話ではありません。どちらも正しいのです。どんな公理を採用するか、出発点をどこにおくか、それだけの問題です。それによって、のちのち展開される理論は変わってきます。
命題・定理とは
命題(propositon)とは、数学的に真(true)か偽(false)がはっきりとする文章のことです。
数学では命題を対象にしますし、命題とならない日常的な文章は数学の対象ではありません。
例えば、「6は偶数でない」は命題です。命題は、正しくなくても命題と呼ばれます。これは偽の命題です。また、「6月は雨ばかりです」は文章ではありますが、(数学における)命題ではありません。6月、雨ばかりという言葉の意味を数学的に定義すれば、命題となりますが……。
命題のうち、真であると広く知られたものを定理(Theorem)と呼びます。定理は命題の一種です。
中間値の定理:関数 f を閉区間[a, b]上で連続な関数とすると、f(a) < s < f(b) を満たす実数 s に対して、f(x) = s を満たす実数 x が少なくとも一つ存在する。
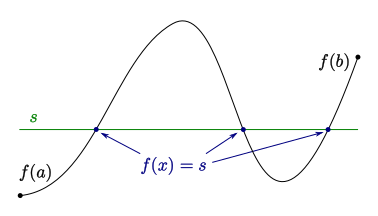
引用:中間値の定理 – Wikipedia Stephan Kulla
高校までの数学だと、定理は半ば当たり前のものとして紹介されます。証明も一応ついていますが、テストで問われることは稀です。定理は正しいものとして使えば良い、という立場です。
大学数学では、定理に対する扱いが変わります。「~~の定理を証明せよ」というのはよくテストの問題となります。定義によってとりきめられた言葉をもとに、定理の正しさを論理的に示す必要があるのです。
証明とは
証明(proof)とは、命題の真偽を明らかにすることです。「なぜならば~」という証拠ですね。
大学数学の教科書を読むときは、定義は「ふんふん、具体例は?」と飲み込み、命題は「来たな、言ってることは本当か?」と見て、命題をひとつひとつ証明していくのが良いでしょう。書いてあることをそのまま飲み込まず、わからないことにはつっかかり、疑ってかかります。
話をまとめると
定義:自然数\(n\) が偶数であるとは、\(n\)が2で割り切れることである。
命題:101は偶数である。
証明:上の命題は偽であることを示す。101=2*50+1と表せる。よって、101は偶数ではない。
というのが具体例。
大学の数学の教科書を読むときは、定義・命題・証明が何なのか理解し、それらと戦っていく必要があります。
僕はそれを知らず微積分学・線形代数学に挑み、大学1年のときは数学がよくわからないままでした。
そのよくわからなさがクリアされたのが、大学2年、集合論を舞台に論理学・証明の練習をしてからでした。
というわけで、証明の練習として、集合論入門の記事を書いていきたいと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
講談社
売り上げランキング: 249,707