正弦定理の三角形の面積による証明

どうも、木村（@kimu3_slime）です。

今回は、正弦定理の三角形の面積による証明を紹介します。

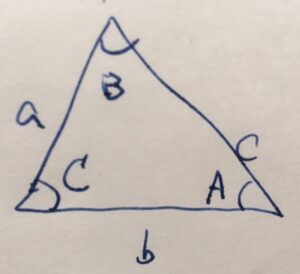
どんな三角形についても、その辺の長さ\(a,b,c\)、対応する角度\(A,B,C\)について

\[\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}\]

という等式が成り立ちます。つまり、辺の長さとその向かい合う辺のサインの比は常に一定です。これを正弦定理（law of sines）と呼びます。

今回は、これを三角形の面積から証明していきましょう。

この三角形の面積\(S\)は、サインを用いると

\[S= \frac{1}{2}bc \sin A\]

\[S= \frac{1}{2}ca \sin B\]

\[S= \frac{1}{2}ab \sin C\]

と表せます。

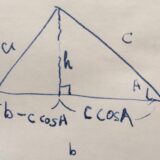
例えば最初の等式を示しましょう。\(b\)を底辺とした高さを\(h\)し、\(c\)を斜辺として見ればサインの定義から\(\frac{h}{c}= \sin A\)です。よって、三角形の面積の公式から、\(S = \frac{1}{2}bh =\frac{1}{2}bc\sin A\)が示せました。他の2つも同様です。

複数の視点から三角形の面積が表せるわけですが、どれも同じ三角形の面積で、それらは等しいです。1つ目の等式と2つ目の等式を連立させれば、

\[ \frac{1}{2}bc \sin A= \frac{1}{2}ca \sin B\]

となり、共通する\(\frac{1}{2}c\)で割れば

\[ b \sin A= a \sin B\]

で、\(\frac{\sin A}{a} = \frac{\sin B}{b}\)が得られました。

同様にして、2つ目と3つ目の等式の連立から\(\frac{\sin B}{b} = \frac{\sin C}{c}\)が示せるので、正弦定理が成り立つことがわかりました。

以上、正弦定理の三角形の面積による証明を紹介してきました。

三角形の面積とサイン（角度）の関係を知っていれば、正弦定理はそこから簡単に導ける性質と言えますね。

木村すらいむ（@kimu3_slime）でした。ではでは。