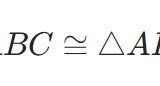どうも、木村(@kimu3_slime)です。
今回は、逆向きの進行波の重ね合わせで定常波ができることの証明を紹介します。
進行波とは、三角関数の形が空間的に進行する波です。横波とも。
\(u(x,t)= \sin (t-x)\)
定常波は、山と谷が起こる場所がとどまった波です。縦波とも。
\(v(x,t)= \sin t \cdot \sin x\)
逆向きの進行波がうまく重なると、定常波が生まれます。
これは電子レンジの加熱の仕組みに利用されているものです。
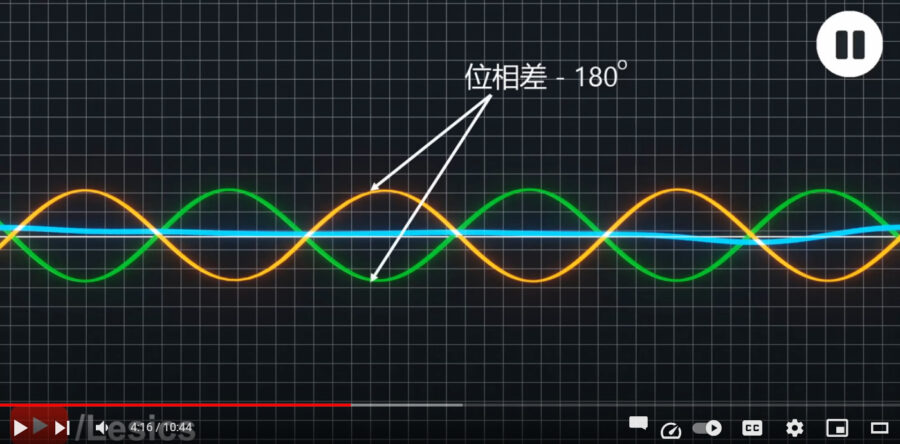
画像引用:電子レンジ|物理的仕組みを解説 –Lesics 日本語
では、逆向きの進行波が重なると、定常波が生まれることを数学的に証明しましょう。
\(u_1(x,t)= \sin (x-t)\)と\(u_2(x,t)= \sin (x+t)\)について考えます。\(t\)の符号が異なるので、これらの波は逆向きに進んでいます。
それらを足して、三角関数の加法定理(和積の公式)
\[\sin A+\sin B = 2 \sin(\frac{A+B}{2}) \cos(\frac{A-B}{2})\]
を用いれば
\[\begin{aligned} &\sin (x-t)+\sin (x+t)\\ &= 2 \sin(\frac{x-t+x+t}{2}) \cos(\frac{x-t-(x+t)}{2}) \\ &=2 \cos(-t)\sin x\end{aligned}\]
と定常波を導くことができました。
\(\sin x\)という形状が空間的に固定されていて、その振幅が\(\cos (-t)\)によって変化しています。振幅も2つの波が重なったことにより2倍になっていますね。
以上、逆向きの進行波の重ね合わせで定常波ができることの証明を紹介してきました。
定常波は動かない特殊な波に見えるかもしれませんが、進行波が重なった結果できるものと見れるのは面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Elementary Geometry for College Students 5th (Fifth) Edition byAlexander
¥13,970 (中古品)