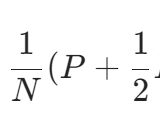どうも、木村(@kimu3_slime)です。
「\(\frac{x^2}{x}\)や\(x/x\)」のグラフを描け、その定義域をどう捉えるか、\(x=0\)で定義できるかといった問題を目にしました。
今回は、こうした関数の定義域の捉え方や、除去可能な特異点について紹介していこうと思います。
定義域は数式から勝手に決まるものではない
「\(f(x)= \frac{x^2}{x}\)のグラフを描け」という問題を考えましょう。
\(x \neq 0\)のときは\(f(x)=x\)となるので、原点をのぞいて考えれば、グラフは直線です。
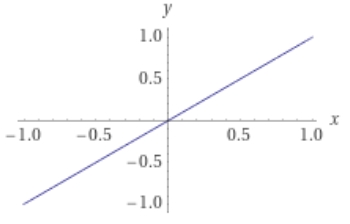
画像引用:Wolframalpha
「\(f(x)= \frac{x^2}{x}\)のグラフを描け」という形の問題はよく見かけますが、関数が定義されている範囲、定義域を明示してないと問題として条件に不足があり、あいまいさがあります。
しばしば見られる勘違いが、「\(f(x)= \frac{x^2}{x}\)は分母に\(x=0\)を代入できない。だから\(x=0\)では定義できず、\(x \neq 0\)となる実数が定義域である」といったものです。
確かに、\(f(x) =\frac{x^2}{x}\)という数式一本によって、可能な限り大きな実数内の定義域を探せば、\(x \neq 0\)となります。しかし、それは\(x=0\)での値をどう決めるか、定義できないと言えるような事実ではありません。実際、
\[f_0(x)= \begin{cases}\frac{x^2}{x}\ & (x \neq 0 )\\0 & (x=0)\end{cases}\]
や
\[f_1(x)= \begin{cases}\frac{x^2}{x}\ & (x \neq 0 )\\1 & (x=0)\end{cases}\]
といった関数を考えることができます。これらの関数は\(x=0\)で定義されており、定義域は実数全体です。
「\(f(x)= \frac{x^2}{x}\)のグラフを描け」という問題では、\(x=0\)での値は未定義です。その時点では、定義域は\(x \neq 0\)と考えることもあるでしょう。
「常識的に考えて」「空気を読んで」捉えればそれはひとつの定義域ですが、\(x=0\)で定義された関数を考えることもできることに注意しましょう。
「\(f(x)= \frac{x^2}{x}\)がそのままでは\(x=0\)で定義されていない(できないように見える)」ことと、ゼロ割り算が定義できないことは意味が違います。
除去可能な特異点
以上で見てきたように、\(f(x)= \frac{x^2}{x}\)という数式だけでは、\(x=0\)での値は定義されていません。
そこで
\[f_0(x)= \begin{cases}\frac{x^2}{x}\ & (x \neq 0 )\\0 & (x=0)\end{cases}\]
と\(x=0\)での値を0と定めると、関数\(f_0\)は\(x=0\)において連続となります。ラフにいえば、直線\(y=x\)とつながったグラフになります。
関数が\(x=0\)で連続であるとは、左極限と右極限が存在し、それらが一致していることです。
\[\lim_{x \nearrow 0}f_0(x)= f(0)\]
\[\lim_{x \searrow 0}f_0(x)= f(0)\]
実際、\(x=0\)における極限を考えるとき、\(x\)は0に近いが0でない数として考えているので、\(f_0(x)=x\)となるので、極限を取れば0に近づきます。
一般に、複素解析の理論では、\(f(z) = \frac{z^2}{z}\)のようなそのままでは分母が未定義となり、それ以外ではなめらかな(複素微分可能な)関数を考えるとき、\(z=0\)を孤立特異点と呼びます。特異点とは、他のなめらかな部分とは挙動が違う点の総称です。
特に、\(f(z) = \frac{z^2}{z}\)は\(f(0)=0\)と定義することで、複素数全体で微分可能な関数となります。このような孤立特異点は、除去可能特異点と呼ばれます。見かけ上は特異点だけれども、特異点がなくなるような関数に拡張できるわけですね。
実数の範囲でも、似た用語を考えることができます。
\[f_1(x)= \begin{cases}\frac{x^2}{x}\ & (x \neq 0 )\\1 & (x=0)\end{cases}\]
という関数を考えると、\(f_1\)は原点\(x=0\)において連続ではありません。このような点\(x=0\)を不連続点と呼びましょう。
この関数は\(x=0\)での値を
\[f_0(x)= \begin{cases}\frac{x^2}{x}\ & (x \neq 0 )\\0 & (x=0)\end{cases}\]
と変更することで、連続な関数に変わります。このような不連続点は、除去可能な不連続点と呼ばれるものです。
除去可能な特異点、不連続点との違いを考えるために、反比例\(g(z) = \frac{1}{z}\)について考えましょう。
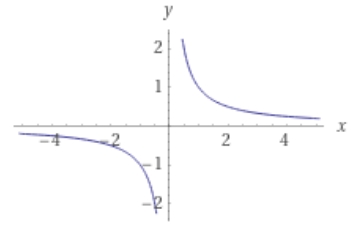
画像引用:WolframAlpha
\(z=0\)は孤立特異点ですし、\(z=0\)での値を何かしら定義すればそれは不連続点でもあります。反比例のグラフを考えればわかりますね。
この関数は、\(g(0)\)をどのような値で定義しても、\(z=0\)で微分可能になりません。このような孤立特異点は、極と呼ばれます。
また、実数値関数として見ても、
\[\lim_{x \nearrow 0}g(x)= -\infty\]
\[\lim_{x \searrow 0}g(x)= \infty\]
と極限が有限値として存在しないので、\(g(0)\)を\(x=0\)であるように定義することはできません。
一般に、右極限も左極限も有限値として存在しないとき、\(x=0\)は本質的な不連続点であると呼ばれます。
\(f(x)=\frac{x^2}{x}\)と\(g(x)= \frac{1}{x}\)の特異性、不連続性を見比べると、その違いがわかりやすいのではないでしょうか。
どちらの関数も、\(x=0\)での値を定義できないわけではありません(定義せずにグラフを描くこともあるでしょうが)。しかし、前者は連続であるように値を定義することができるけれども、後者はどうやっても連続にはならないというわけです。
関数の定義に関するよくある誤解
最後に少し補足をしましょう。
「\(f(x)= \frac{x^2}{x}\)は\(x=0\)において定まっていない(不定)。だから、任意の値を取れる」という表現はよく見られますが、これは間違いです。
\(f(0)\)の値は確かにどのような数として定めても良いのですが、それはただひとつの値である必要があります。例えば、「\(f(0)=0\)かつ\(f(0)=1\)」と定めることはできないのです。これは関数の定義「変数\(x\)に対してただひとつの数\(f(x)\)を対応させる規則」に反するものなので。
また、多項式の割り算(除法)としては\(\frac{x^2}{x}=x\)です。なぜなら、\(x^2 = x\times x +0\)が成り立つので(除法の定義)。
多項式における不定元\(x\)と関数における変数\(x\)は、別物です。
「\(\frac{x^2}{x}=x\)は\(x=0\)のケースを考えると成り立たない」と述べるのは、それを関数として見ているならば正しいし、多項式として見ているならば誤りです。
数(関数の値)の割り算と、多項式の割り算は別物なので注意しましょう。
参考:河合塾・大竹先生による 先生方のための徹底入試対策講座 – 第35回 0 で割ってもいいのですか?
以上、x^2/ xの定義域、x=0で定義できるかという問題を考え、関数の定義域の考え方、除去可能な特異点について紹介してきました。
\(\frac{x}{x}\)や\(\frac{\sin x}{x}\)でも同じような問題が起こりますが、今回の話と同じです。関数の定義や定義域の考え方が深まり、疑問が解消されれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
ローラン展開とは:求め方、孤立特異点の分類(極、除去可能特異点、真性特異点)