どうも、木村(@kimu3_slime)です。
今回は、Juliaで散布図を描き、相関係数を求める方法を紹介します。
準備
RDatasets, StatsPlotsを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("RDatasets") Pkg.add("StatsPlots") |
準備として、以下のコードを実行しておきます。
1 | using Statistics, RDatasets, StatsPlots |
散布図、相関図を描く
RDatasets.jlから、アイリス(iris, アヤメ)のデータを使いましょう。
1 | iris = dataset("datasets","iris") |
150 rows × 5 columns
| SepalLength | SepalWidth | PetalLength | PetalWidth | Species | |
|---|---|---|---|---|---|
| Float64 | Float64 | Float64 | Float64 | Cat… | |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
「@df データフレーム scatter(変数名1, 変数名2)」で2つのデータに関する散布図(scatter plot)が描けます。
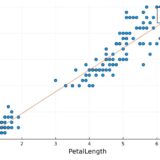
がく片の長さと花弁の長さの散布図は次の通りです。
1 | @df iris scatter(:SepalLength, :PetalLength) |
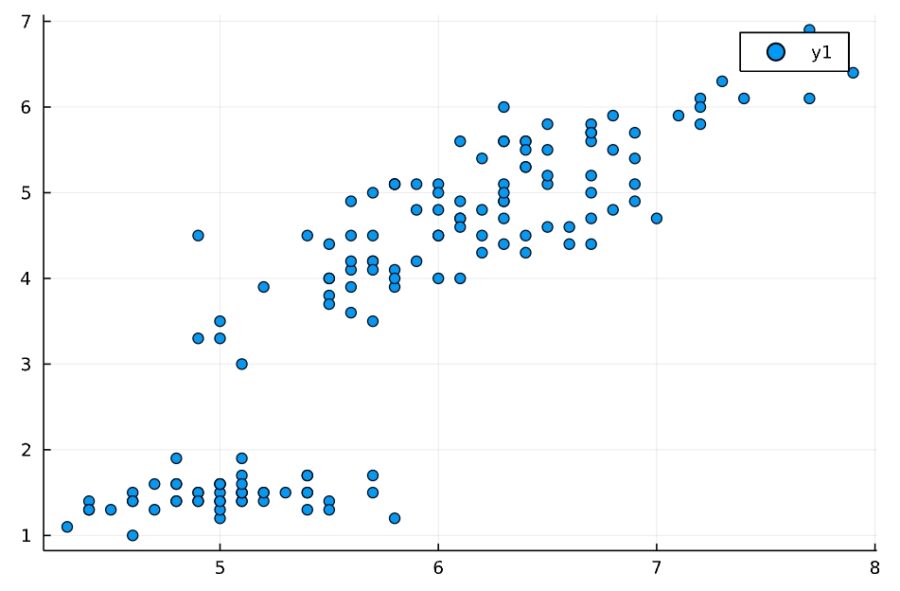
第1成分が横軸(x軸)、第2成分が縦軸(y軸)です。
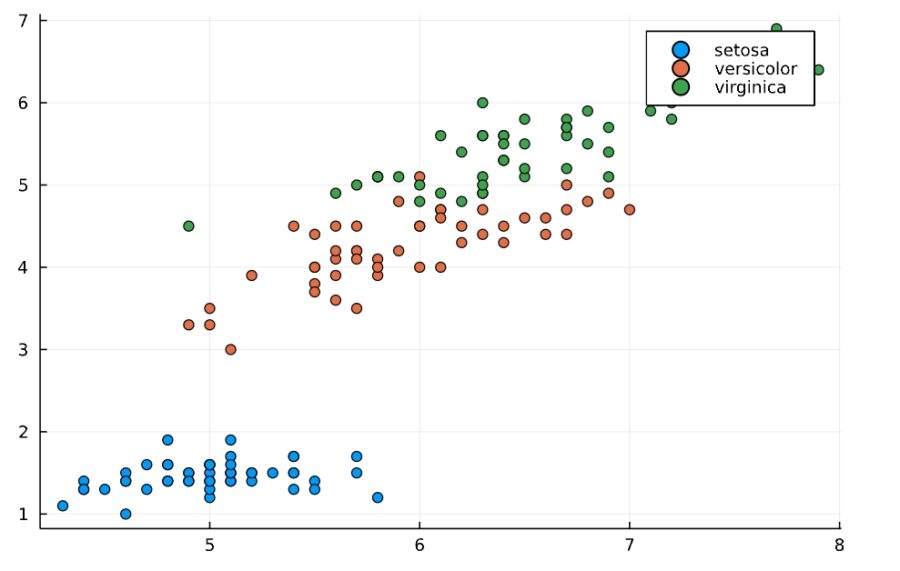
オプションとして品種の情報を与えることで、品種ごとに色分けしてくれます。
1 | @df iris scatter(:SepalLength, :PetalLength, group=:Species) |
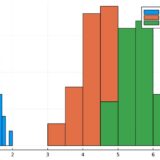
データフレームに含まれるすべての変数について、散布図、相関図の組み合わせを並べた図(散布図行列、相関図行列)を描きましょう。
「@df データフレーム corrplot(cols(列の指定))」です。
1 | @df iris corrplot(cols(1:4), grid = false) |
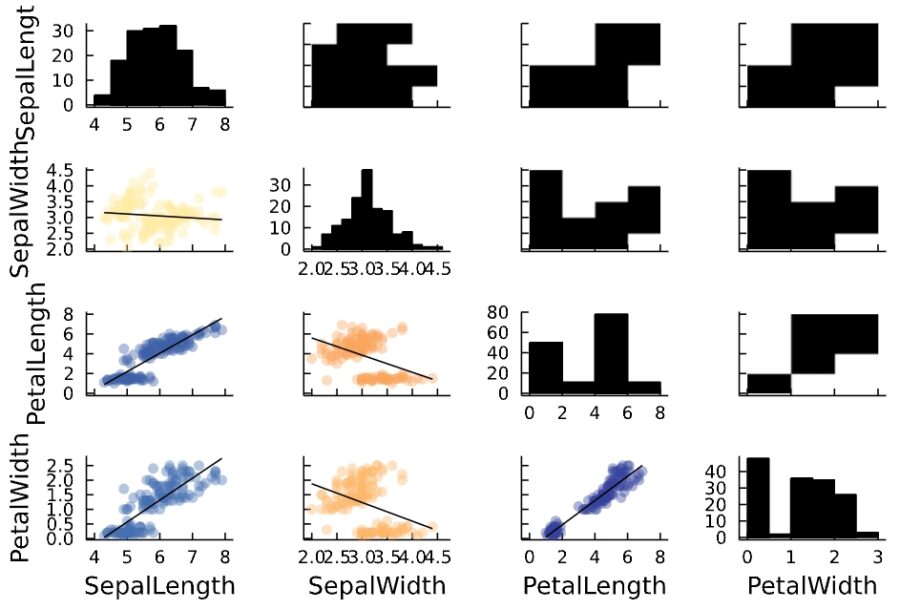
図の左下側が相関図(correlation plot)、対角成分が1次元のヒストグラム、右上側が2次元のヒストグラムです。
相関図では、相関係数が1に近いときは青、0に近いときは黄色、-1に近いときは赤で表示されています。また、相関図に書かれている直線は、データを近似する回帰直線(regression line)です。
特に、花弁の長さ(PetalLength)と花弁の幅(PetalWidth)では強い正の相関があることが読み取れます。
がく片の幅(SepalWidth)と花弁の幅(PetalWidth)・花弁の長さ(PetalLength)では、負の相関を示す色が出て、回帰直線の傾きも負です。しかし、これは散布図を見る限り、データとマッチするとは言い難いことに注意しましょう。
相関図行列でも、品種ごとにプロットできます。
1 | @df iris corrplot(cols(1:4), group=:Species, grid = false) |

各品種ごとに回帰直線が引かれています。SepalWidthについては、品種ごとにはPetalWidth・PetalLengthと弱い正の相関がありそうですね。
相関係数を求める方法
「@df データフレーム cor(変数名1, 変数名2)」で、(ピアソンの積率)相関係数(correlation coefficient)が求められます。
1 | @df iris cor(:PetalLength, :PetalWidth) |
1 | 0.9628654314027961 |
相関係数の定義は次の通り。
\[ \begin{aligned}\mathrm{cor}(x,y) = \frac{\mathrm{cov}(x,y)}{\mathrm{std}(x)\mathrm{std}(y)}\end{aligned} \]
\[ \begin{aligned}\mathrm{cov}(x,y) = \frac{1}{n-1}\sum _{i=1}^n (x_i -\mathrm{mean}(x))(y_i – \mathrm{mean}(y))\end{aligned} \]
平均と標準偏差について:Juliaでデータのヒストグラム、箱ひげ図を描き、平均、中央値、分散を求める方法
同様に、「cov」で(不偏)共分散(covariance)が計算できます。
1 | c_xy = @df iris cov(:PetalLength, :PetalWidth) |
1 | 1.2956093959731547 |
相関係数、共分散、標準偏差の関係を検算してみると、確かにほぼ一致していることがわかります。
1 2 3 | s_x = @df iris std(:PetalLength) s_y = @df iris std(:PetalWidth) c_xy /(s_x * s_y) |
1 2 3 | 1.7652982332594664 0.7622376689603466 0.9628654314027963 |
特定の変数だけでなく、すべての変数についてまとめて相関、共分散、分散を計算できます。それぞれ相関行列(correlation matrix)、分散・共分散行列(variance-covariance matrix)と呼ばれるものです。
1 | @df iris cor(cols(1:4)) |
1 2 3 4 5 | 4×4 Matrix{Float64}: 1.0 -0.11757 0.871754 0.817941 -0.11757 1.0 -0.42844 -0.366126 0.871754 -0.42844 1.0 0.962865 0.817941 -0.366126 0.962865 1.0 |
1 | @df iris cov(cols(1:4)) |
1 2 3 4 5 | 4×4 Matrix{Float64}: 0.685694 -0.042434 1.27432 0.516271 -0.042434 0.189979 -0.329656 -0.121639 1.27432 -0.329656 3.11628 1.29561 0.516271 -0.121639 1.29561 0.581006 |
最後に、各品種ごとに相関図を描き、相関行列を求めてみましょう。
1 2 3 4 5 6 7 | iris_group=groupby(iris, :Species) for i in 1:3 display(iris_group[i][1,5]) display(@df iris_group[i] corrplot(cols(1:4), grid = false)) display(@df iris_group[i] cor(cols(1:4))) end |
1 | CategoricalArrays.CategoricalValue{String, UInt8} "setosa" |
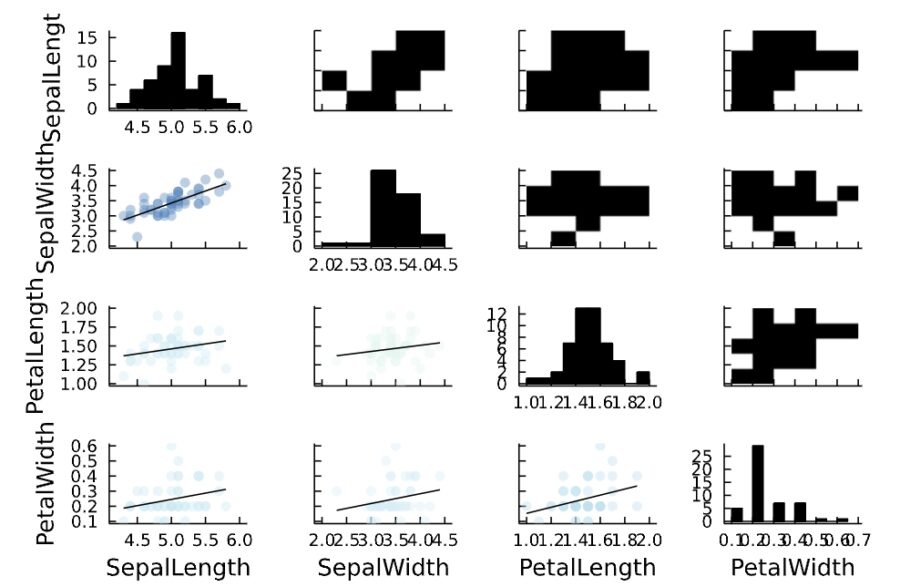
1 2 3 4 5 6 | CategoricalArrays.CategoricalValue{String, UInt8} "setosa" 4×4 Matrix{Float64}: 1.0 0.742547 0.267176 0.278098 0.742547 1.0 0.1777 0.232752 0.267176 0.1777 1.0 0.33163 0.278098 0.232752 0.33163 1.0 |
1 | CategoricalArrays.CategoricalValue{String, UInt8} "versicolor" |
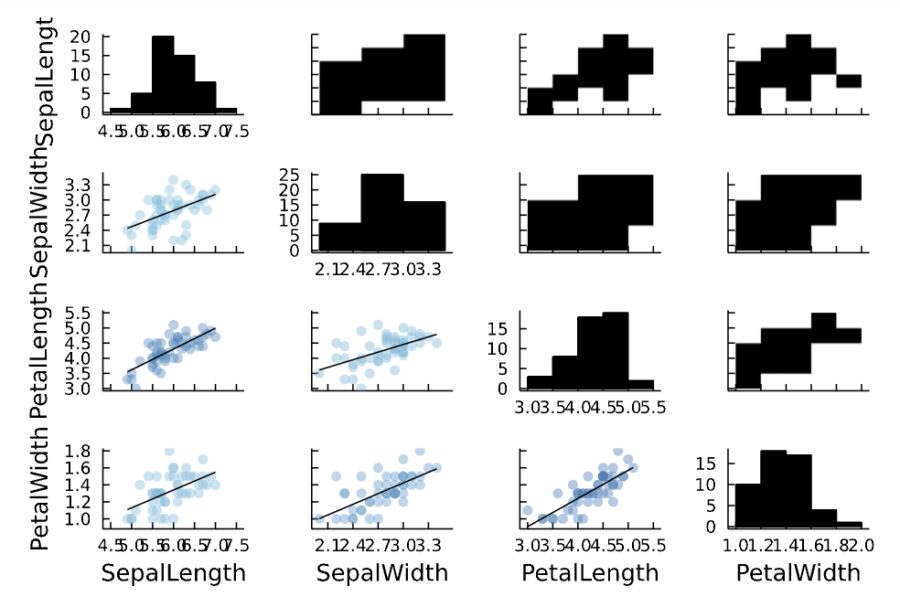
1 2 3 4 5 | 4×4 Matrix{Float64}: 1.0 0.525911 0.754049 0.546461 0.525911 1.0 0.560522 0.663999 0.754049 0.560522 1.0 0.786668 0.546461 0.663999 0.786668 1.0 |
1 | CategoricalArrays.CategoricalValue{String, UInt8} "virginica" |
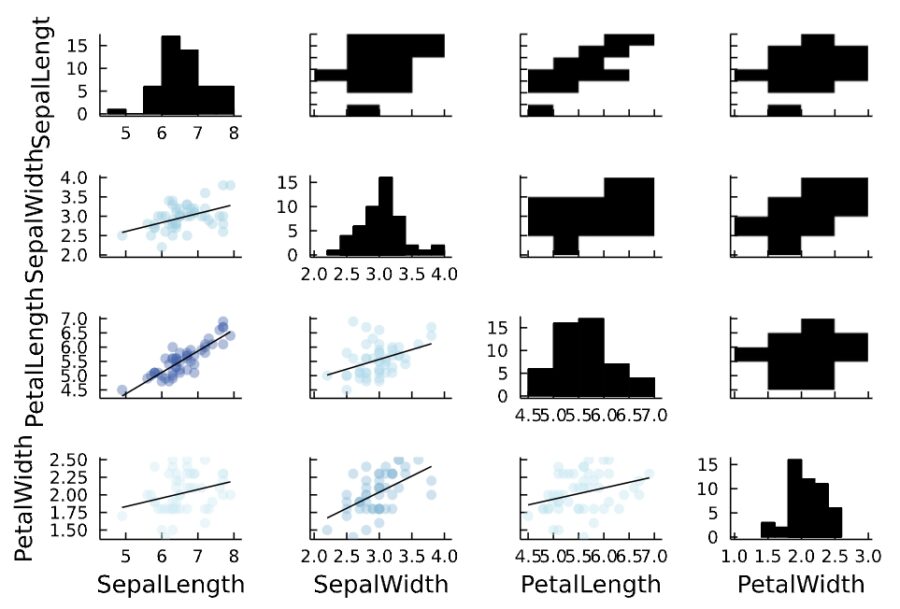
1 2 3 4 5 | 4×4 Matrix{Float64}: 1.0 0.457228 0.864225 0.281108 0.457228 1.0 0.401045 0.537728 0.864225 0.401045 1.0 0.322108 0.281108 0.537728 0.322108 1.0 |
いずれの品種でも、すべての変数について、弱い相関~強い相関がありそうなことが、散布図と相関係数からわかりますね。
品種全体を扱った最初の結果は、線形的な相関関係では必ずしも測れないものだった、ということがこの例から読み取れます。がく片の幅という変数の違いより、品種の違いの方が大きく影響して、関係が読み取りづらかったわけです。
以上、Juliaで散布図を描き、相関係数を求める方法を紹介してきました。
相関係数を計算するのは簡単ですが、データと散布図を見て、変数間にどんな関係性があるのか・ないのか予想することは大事です。必ず散布図を描いて、その考察に相関係数を利用すると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Juliaでデータのヒストグラム、箱ひげ図を描き、平均、中央値、分散を求める方法
Pythonで統計量関数(平均、中央値、分散、相関係数)を作り、可視化しよう