どうも、木村(@kimu3_slime)です。
今回は、Julia(Glaphs)で2部グラフの最大マッチングを求め、図示する方法を紹介します。
前提知識:Julia(Graphs)で2部グラフかどうかを判別し、図示する方法、Julia(Graphs)で最大フロー問題を解き、図示する方法
準備
Graphs, GraphPlot, Colors, GraphsFlowsを使うので、持っていなければインストールしておきましょう。
1 2 3 4 5 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") Pkg.add("GraphsFlows") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors |
2部グラフの最大マッチングを求め、図示する方法
最大マッチングとは、求め方
グラフ\(G= (V,E)\)のマッチング\(M\)とは、辺の部分集合\(M\subset E\)であって、それらの辺が共通する端点を持たないことです。
一般に、マッチングには複数の可能性があります。その中で、辺の個数が最も多いマッチングを最大マッチング(Maximum cardinality matching)と呼びます。
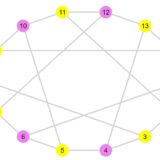
以下の図で示したグラフにおいて、赤い辺が最大マッチングの例です。

最大マッチングを求める方法は、いくつか知られています。
特に2部グラフにおける最大マッチング問題は、最大フロー問題に帰着させることができます。
- 2部グラフの頂点の集合を分けた集合を\(V_1,V_2\)とする。
- \(V_1\)から\(V_2\)へと向きをつけた辺を持つグラフを考える。
- ソースとシンクとして新たな頂点2つを加え、ソースからは\(V_1\)の各頂点へ、\(V_2\)の各頂点からはシンクへの向きをつけた辺を加える。
- すべての辺のキャパシティを等しく1とする。
- こうしてできるネットワークの最大フロー問題の解が、元の2部グラフの最大マッチングに対応する。
参考:離散数学入門#11: マッチング(2):最大マッチングを見つける2つの方法 – Momoko Hayamizu
今回はこの方法に従って、最大マッチングを求めましょう。
簡単な例
まず、2部グラフの描写に用いる関数を導入します。
1 2 3 4 5 6 | function cplot(G,source,sink,C) vcolor = [colorant"turquoise" for i in 1:nv(G)] vcolor[source] = colorant"yellow" vcolor[sink] = colorant"violet" gplot(G, nodelabel= 1:nv(G), edgelabel= C, nodefillc=vcolor, layout=circular_layout) end |
1 2 3 4 5 6 7 | function cfplot(G,source,sink,C,F) vcolor = [colorant"turquoise" for i in 1:nv(G)] vcolor[source] = colorant"yellow" vcolor[sink] = colorant"violet" CF = [(C[i],F[i]) for i in 1:ne(G)] gplot(G, nodelabel= 1:nv(G), edgelabel= CF, nodefillc=vcolor, layout=circular_layout) end |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | function bipartite_plot(G) if is_bipartite(G) == false display("2部グラフでない") display(gplot(G, nodelabel= 1:nv(G), layout=circular_layout)) else vcolor =Vector{RGB}(undef, nv(G)) for i in 1:nv(G) if bipartite_map(G)[i] == 0x01 vcolor[i] = colorant"yellow" else vcolor[i] = colorant"violet" end end display("2部グラフである") display(gplot(G, nodelabel= 1:nv(G), nodefillc=vcolor, layout=circular_layout)) end end |
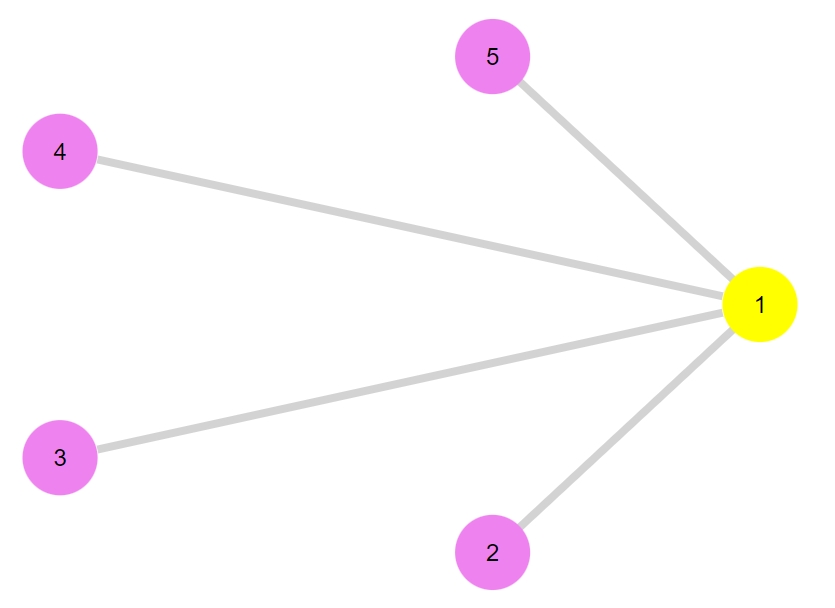
最初に考えるのは、次の簡単な2部グラフです。
1 2 | G1 = star_graph(5) bipartite_plot(G1) |
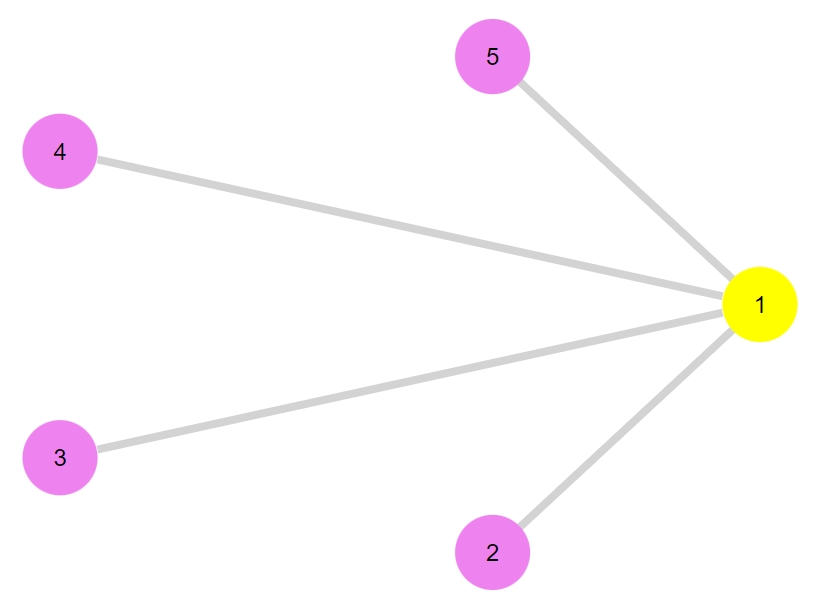
これに新たな頂点(ソースとシンク)を加え、有向グラフを作りましょう。
頂点をグループ分けする集合\(V_1,V_2\)は、「bipartite_map」で求められます。
頂点数を2つ増やした有向グラフを作り、元のグラフの\(V_1,V_2\)の情報を使って有向辺を加え、ソースとシンクに\(V_1,V_2\)を対応させる辺を加えます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | DG = DiGraph(nv(G1)+2) V1 = [ i for i in 1:nv(G1) if bipartite_map(G1)[i] == 0x01] V2 = [ i for i in 1:nv(G1) if bipartite_map(G1)[i] == 0x02] for i in V1 add_edge!(DG,nv(G1)+1, i) end for i in V2 add_edge!(DG,i, nv(G1)+2) end for i in 1:ne(G1) if collect(edges(G1))[i].src in V1 add_edge!(DG,collect(edges(G1))[i].src, collect(edges(G1))[i].dst) else add_edge!(DG,collect(edges(G1))[i].dst, collect(edges(G1))[i].src) end end gplot(DG, nodelabel= 1:nv(DG), layout=circular_layout) |

\(6\)がソース、\(7\)がシンクです。
以前作った最大フローをプロットする関数を使い、すべてのキャパシティを1としたネットワークの図示をしましょう。
1 2 3 4 5 6 7 8 9 | function capacity_matrix(G, capacity) size = nv(G) capacity_matrix = zeros(size,size) edges = collect(Graphs.edges(G)) for i in 1:ne(G) capacity_matrix[edges[i].src,edges[i].dst] = capacity[i] end return capacity_matrix end |
1 2 3 4 5 6 7 8 | function flow_vector(G,M) edges = collect(Graphs.edges(G)) vector = zeros(ne(G)) for i in 1:ne(G) vector[i] = M[edges[i].src,edges[i].dst] end return vector end |
1 2 3 4 5 6 7 | function maximum_flow_plot(G,source,sink,capacity) CM = capacity_matrix(G, capacity) total = maximum_flow(G, source, sink, CM)[1] MF = flow_vector(G,maximum_flow(G, source, sink, CM)[2]) display("合計フロー:$total") display(cfplot(G,source,sink,capacity,MF)) end |
1 | C1 = [1 for i in 1:ne(DG)] |
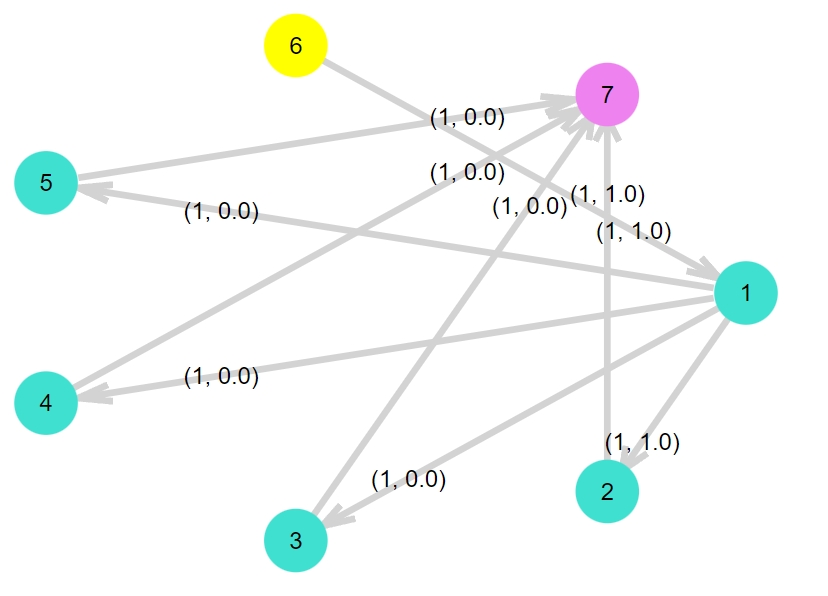
1 | maximum_flow_plot(DG,nv(G1)+1,nv(G1)+2,C1) |
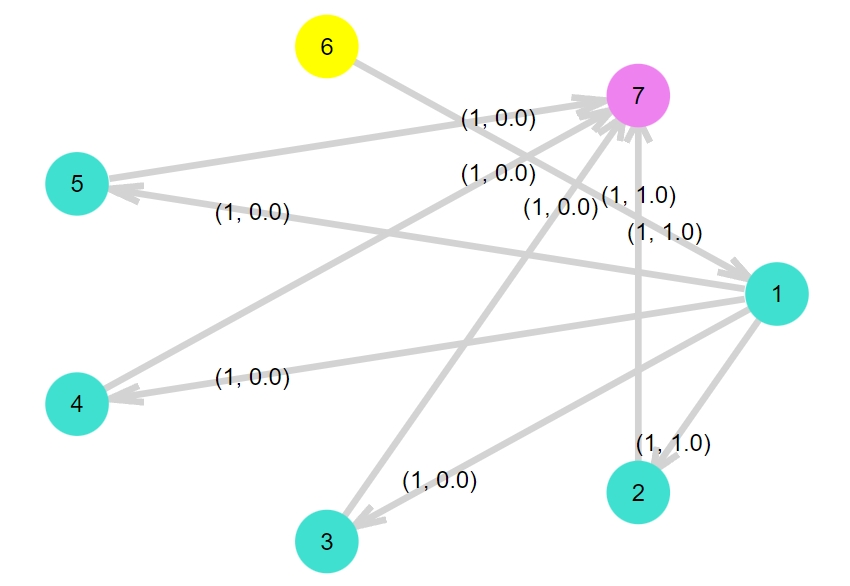
これで最大フローが求められました。
辺にかかれている第2成分の数値がフローであり、それが\(1.0\)である辺が最大マッチングに対応する辺です。
一般化
以上の結果を、一般化した関数を作りましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | function maximum_matching(G) V1 = [ i for i in 1:nv(G) if bipartite_map(G)[i] == 0x01] V2 = [ i for i in 1:nv(G) if bipartite_map(G)[i] == 0x02] DG = DiGraph(nv(G)+2) for i in V1 add_edge!(DG,nv(G)+1, i) end for i in V2 add_edge!(DG,i, nv(G)+2) end for i in 1:ne(G) if collect(edges(G))[i].src in V1 add_edge!(DG,collect(edges(G))[i].src, collect(edges(G))[i].dst) else add_edge!(DG,collect(edges(G))[i].dst, collect(edges(G))[i].src) end end capacity = [1 for i in 1:ne(DG)] CM = capacity_matrix(DG, capacity) MF = flow_vector(DG,maximum_flow(DG, nv(G)+1,nv(G)+2, CM)[2]) return [(collect(edges(DG))[i],MF[i] ) for i in 1:ne(DG)] end |
これで無向2部グラフを与えると、拡大した有向グラフのキャパシティ1のときの最大フローを、辺とフローの組として返してくれます。
1 | maximum_matching(G1) |
1 2 3 4 5 6 7 8 9 10 | 9-element Vector{Tuple{Graphs.SimpleGraphs.SimpleEdge{Int64}, Float64}}: (Edge 1 => 2, 1.0) (Edge 1 => 3, 0.0) (Edge 1 => 4, 0.0) (Edge 1 => 5, 0.0) (Edge 2 => 7, 1.0) (Edge 3 => 7, 0.0) (Edge 4 => 7, 0.0) (Edge 5 => 7, 0.0) (Edge 6 => 1, 1.0) |
元のグラフで図示するには、加えた頂点(ここでは\(6,7\))を含む辺を無視し、フローの値が\(1.0\)となる辺を色付けすれば良いでしょう。
少し複雑ですが、最大マッチングを図示する関数は次のようになります。
「edgecolor」に、最大マッチングの色情報を代入しています。最大フローの辺の端点がソースまたはシンクでなければ、その辺のもとのグラフにおける辺番号(indexin)に、トマト色を指定しました。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | function maximum_matching_plot(G) if is_bipartite(G) == false display("2部グラフでない") display(gplot(G, nodelabel= 1:nv(G), layout=circular_layout)) else vcolor =Vector{RGB}(undef, nv(G)) for i in 1:nv(G) if bipartite_map(G)[i] == 0x01 vcolor[i] = colorant"yellow" else vcolor[i] = colorant"violet" end end edgecolor = [colorant"lightgray" for i in 1:ne(G)] matching_edges = Graphs.SimpleGraphs.SimpleEdge{Int64}[] for i in 1:length(maximum_matching(G)) if ((maximum_matching(G)[i][1].src != nv(G)+1) && (maximum_matching(G)[i][1].dst != nv(G)+1) && (maximum_matching(G)[i][1].src != nv(G)+2) && (maximum_matching(G)[i][1].dst != nv(G)+2)) if maximum_matching(G)[i][2] == 1 if indexin([maximum_matching(G)[i][1]],collect(edges(G)))[1] != nothing edgecolor[indexin([maximum_matching(G)[i][1]],collect(edges(G)))[1]] = colorant"tomato" else edgecolor[indexin([maximum_matching(G)[i][1]],reverse.(collect(edges(G))))[1]] = colorant"tomato" end push!(matching_edges, maximum_matching(G)[i][1]) else end else end end display(matching_edges) display(gplot(G, nodelabel= 1:nv(G), nodefillc=vcolor, edgestrokec=edgecolor, layout=circular_layout)) end end |
これで求める結果が得られました。
1 | maximum_matching_plot(G1) |
1 2 | 1-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 |
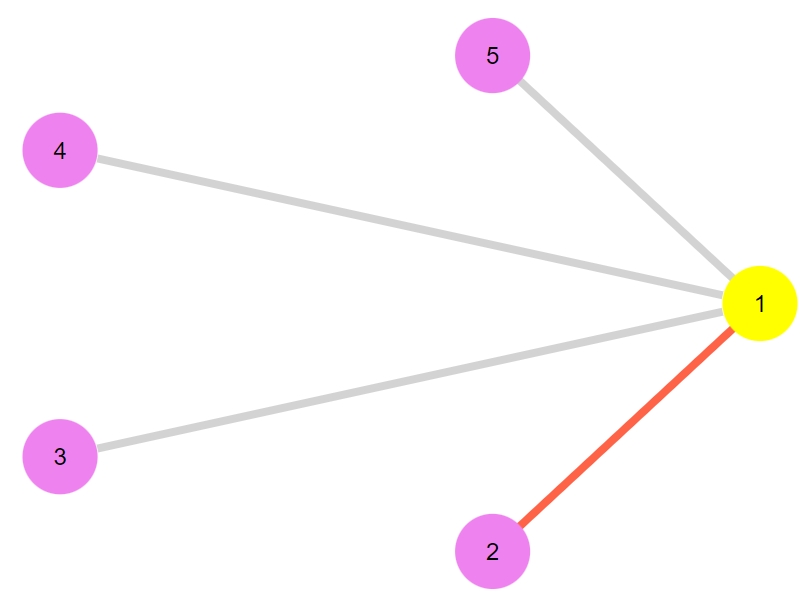
別のグラフを考え、適切な結果が得られるか見てみましょう。
1 | G2 = smallgraph(:heawood) |
1 | maximum_matching_plot(G2) |
1 2 3 4 5 6 7 8 | 7-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 14 Edge 3 => 8 Edge 5 => 6 Edge 7 => 12 Edge 9 => 10 Edge 11 => 2 Edge 13 => 4 |
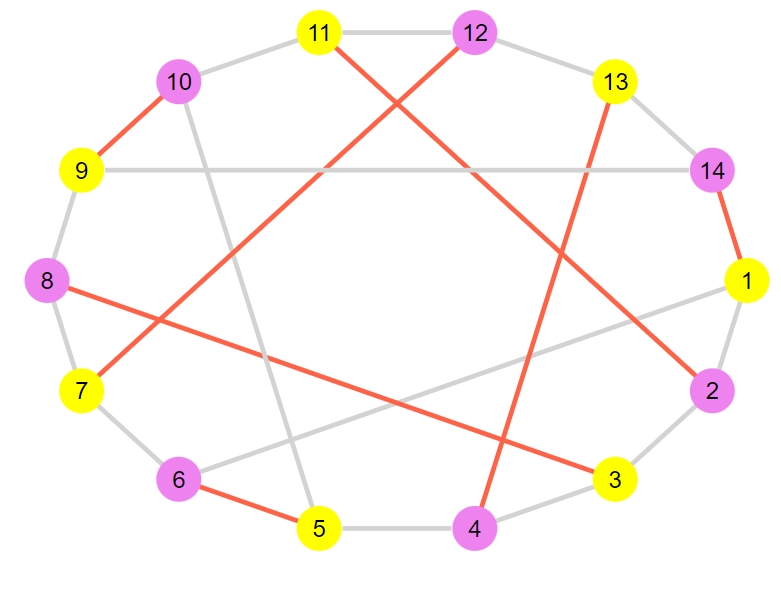
彩色された辺はすべて独立(共通する頂点を含まない)で、すべての頂点がマッチしているので、これは確かに最大マッチングです。
1 2 | G3 = smallgraph(:pappus) bipartite_plot(G5) |
1 2 3 4 5 6 7 8 9 10 | 9-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 18 Edge 3 => 14 Edge 5 => 16 Edge 7 => 6 Edge 9 => 2 Edge 11 => 4 Edge 13 => 12 Edge 15 => 8 Edge 17 => 10 |
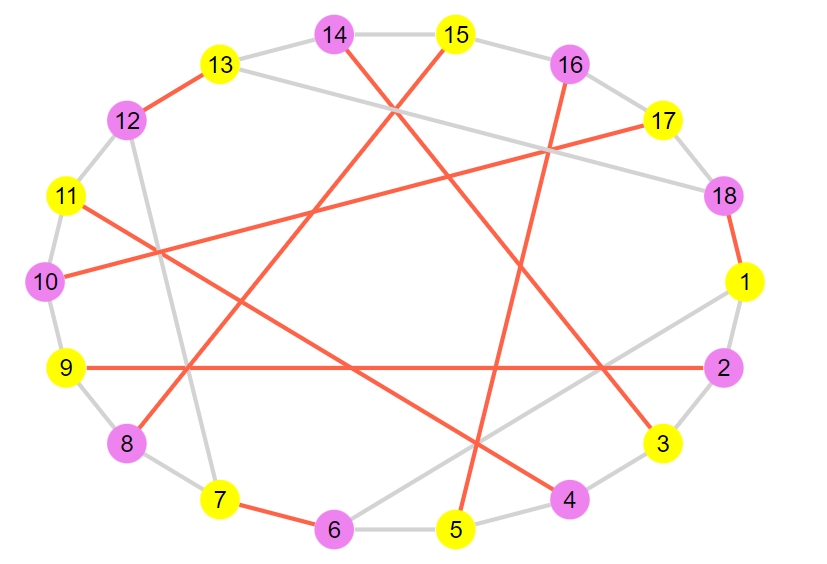
最後に、最大マッチングでもマッチングできない頂点が生まれるようなグラフ(完全マッチングを持たないグラフ)を考えましょう。
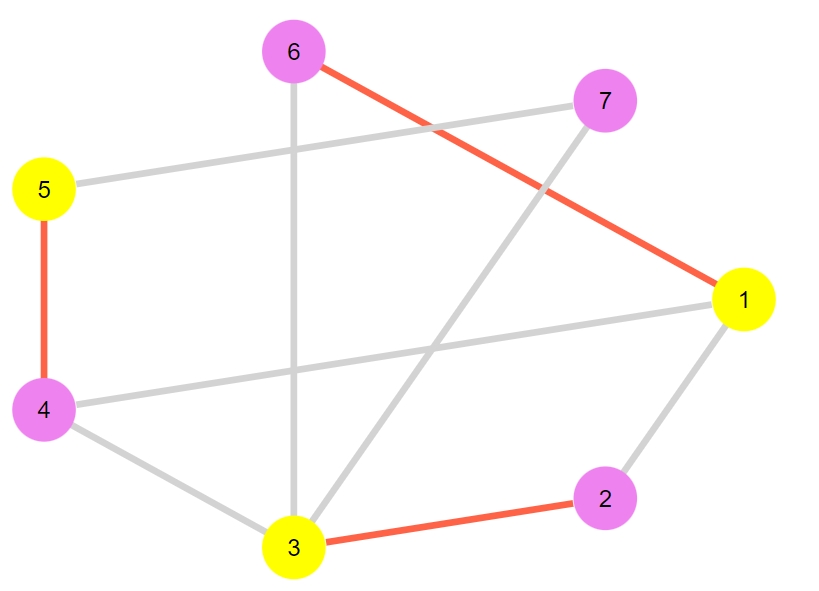
1 2 3 4 5 6 7 8 9 10 | G4 = Graph(7) E4 = [ (1,2),(1,4),(1,6),(2,3),(3,4),(3,6), (3,7),(4,5),(5,7) ] for e in E4 add_edge!(G4, e[1], e[2]) end maximum_matching_plot(G4) |
1 2 3 4 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 6 Edge 3 => 2 Edge 5 => 4 |
以上、Julia(Glaphs)で2部グラフの最大マッチングを求め、図示する方法を紹介してきました。
GraphsMatching.jlというパッケージでも最大マッチングは求められるようなのですが、僕の環境だとうまくインストールできませんでした。
今回の方法ならば最大フローさえ求めれれば使えるので(GraphsFlows.jl)、参考になれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Graphs)で2部グラフかどうかを判別し、図示する方法
Julia(Graphs)で最大フロー問題を解き、図示する方法