どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)で2部グラフかどうかを判別し、図示する方法を紹介します。
前提知識:グラフ理論における2部グラフ、マッチング、結婚定理とは
準備
Graphs, GraphPlot, Colorsを使うので、持っていなければインストールしておきましょう。
1 2 3 4 5 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") Pkg.add("GraphsFlows") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors |
簡単な例
まず、次のサイクルグラフを考えてみます。
1 2 | G1 = cycle_graph(5) gplot(G1, nodelabel= 1:nv(G1), layout=circular_layout) |
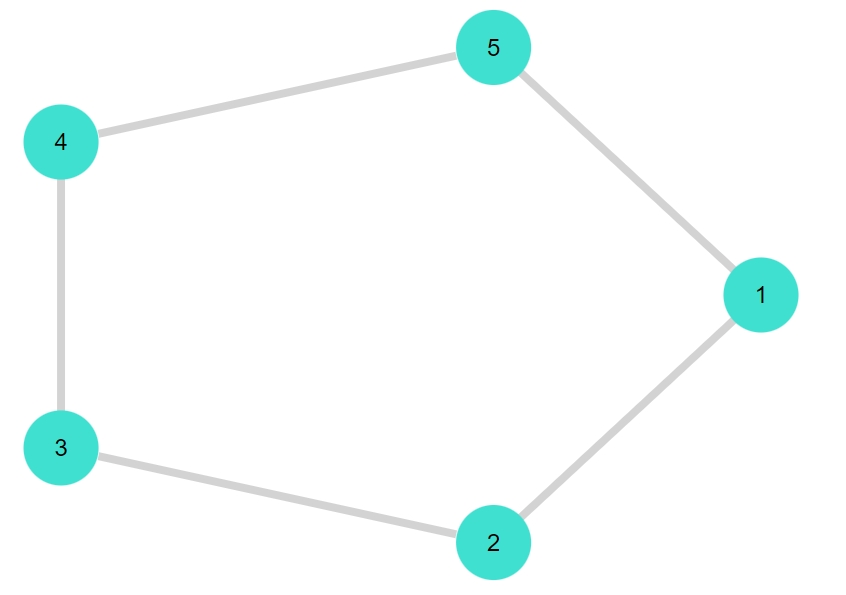
「is_bipartite(グラフ)」で、グラフが2部グラフかどうか、trueかfalseで判定できます。
1 | is_bipartite(G1) |
1 | false |
2部グラフでないとわかりました。
定義を確認しておくと、頂点の集合\(V\)が共通部分を持たない2つの集合\(V_1,V_2\)に分かれていて、\(V_1\)内、\(V_2\)内では異なる頂点が隣接しない(辺がない)グラフを、2部グラフ(bipartite graph)と呼んでいます。
別の例(スターグラフ)を考えましょう。
1 2 3 | G2 = star_graph(5) gplot(G2, nodelabel= 1:nv(G2), layout=circular_layout) is_bipartite(G2) |
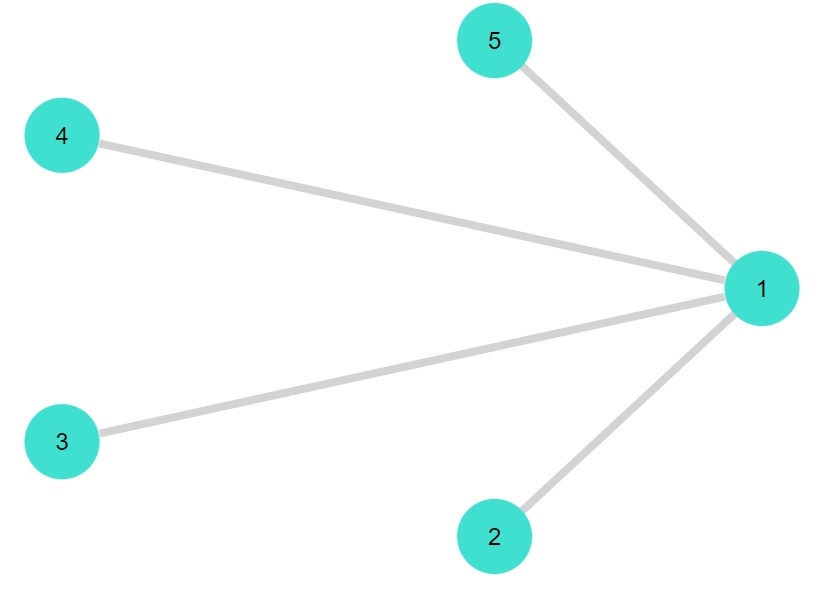
1 | true |
2部グラフであるとわかりました。
2部グラフに対しては、それぞれの頂点がどちらのグループ\(V_1,V_2\)に属するかが「bipartite_map(グラフ)」でわかります。
1 | bipartite_map(G2) |
1 2 3 4 5 6 | 5-element Vector{UInt8}: 0x01 0x02 0x02 0x02 0x02 |
結果は16進数でわかりにくいかもしれませんが、下一桁の違い、1か2かが判定結果です。
この情報を使って、頂点の色塗り分けによって、グループ分けを図示しましょう。
各頂点の色のベクトルを、次のように与えます。もしグループ1ならば黄色、そうでないならば紫です。
1 2 3 4 5 6 7 8 9 | vcolor =Vector{RGB}(undef, nv(G2)) for i in 1:nv(G2) if bipartite_map(G2)[i] == 0x01 vcolor[i] = colorant"yellow" else vcolor[i] = colorant"violet" end end vcolor |

この色ベクトルを使えば、2部グラフのようすがわかりやすくなります。
1 | gplot(G2, nodelabel= 1:nv(G2), nodefillc=vcolor,layout=circular_layout) |
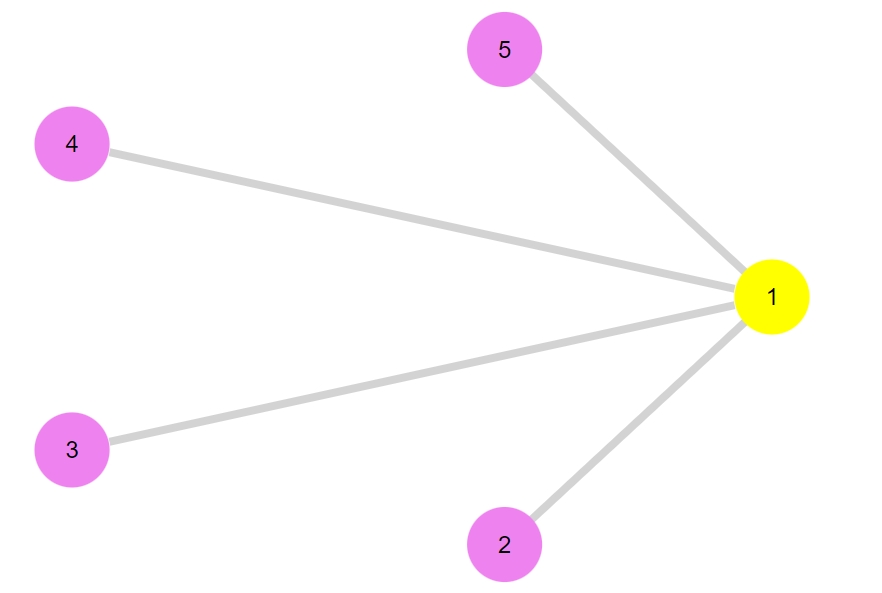
一般化
以上の結果を、一般化した関数を作りましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | function bipartite_plot(G) if is_bipartite(G) == false display("2部グラフでない") display(gplot(G, nodelabel= 1:nv(G), layout=circular_layout)) else vcolor =Vector{RGB}(undef, nv(G)) for i in 1:nv(G) if bipartite_map(G)[i] == 0x01 vcolor[i] = colorant"yellow" else vcolor[i] = colorant"violet" end end display(gplot(G, nodelabel= 1:nv(G), nodefillc=vcolor, layout=circular_layout)) end end |
この関数を使って、いくつかのグラフを2部グラフかどうか判定し、そうであるならば頂点を色分けして図示しましょう。
1 2 | G3 = complete_graph(5) bipartite_plot(G3) |
1 | "2部グラフでない" |

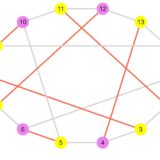
1 2 | G4 = smallgraph(:heawood) bipartite_plot(G4) |
1 | "2部グラフである" |
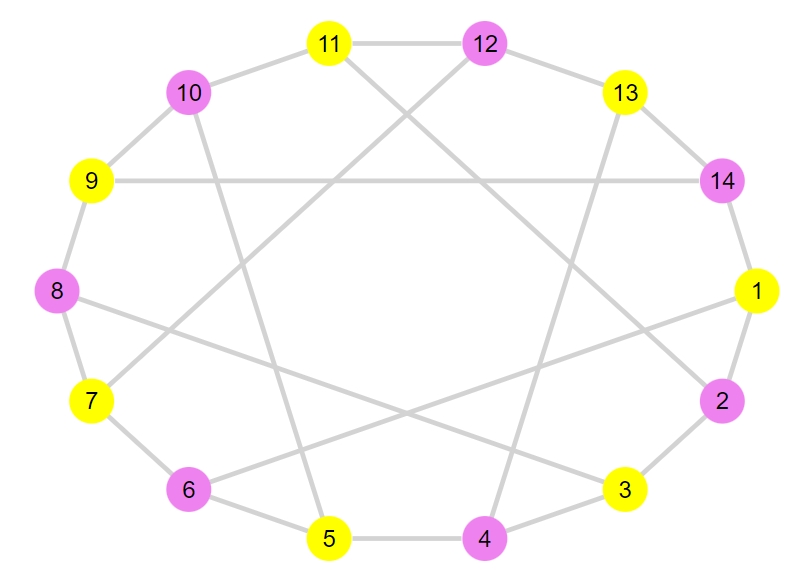
同じグループの中で、隣接する頂点がないことを確認してみてください。
1 2 | G5 = smallgraph(:pappus) bipartite_plot(G5) |
1 | "2部グラフである" |
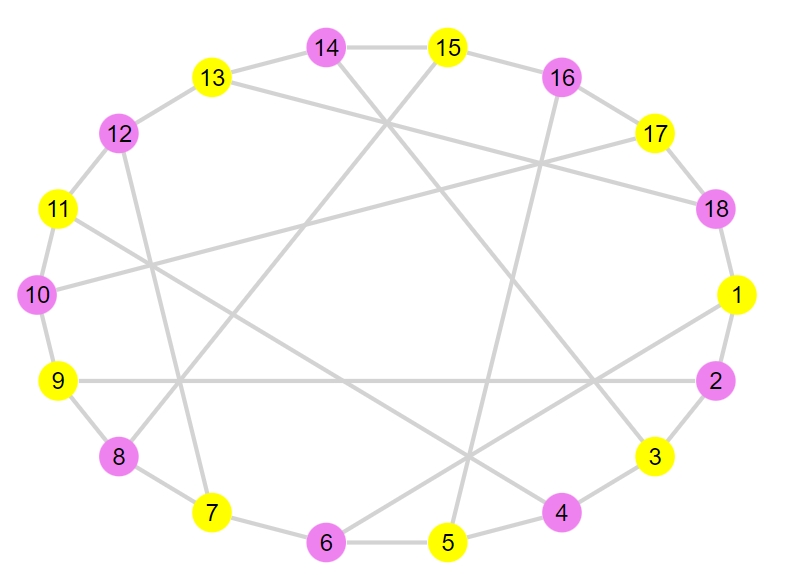
以上、Julia(Graphs)で2部グラフかどうかを判別し、図示する方法を紹介してきました。
明らかに2部グラフとして構成したグラフならばそうと判別しやすいですが、そうでないケースを目で判定するのは難しいです。そこでコンピュータで自動的に判定できると便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)