どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)で全域木を求め、図示する方法を紹介します。
準備
Graphs, GraphPlot, Colorsを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors |
全域木を求め、図示する方法
全域木とは
まず、与えられた連結なグラフ\(G\)の全域木(spanning tree)とは、すべての頂点を保ったまま、辺を部分的に取り除くことで得る木(グラフ)のことです。木(tree)とは、連結であり、サイクルを持たないグラフでした。
一般に、グラフの全域木にはいくつかの候補があります。その中で辺の重みの合計が最も小さいものを、最小全域木(minimum spanning tree; MST)と呼びます。
今回は、各辺の重さが等しいケースでの最小全域木、つまり単に全域木のひとつを求めてみましょう。
簡単な例と関数作り
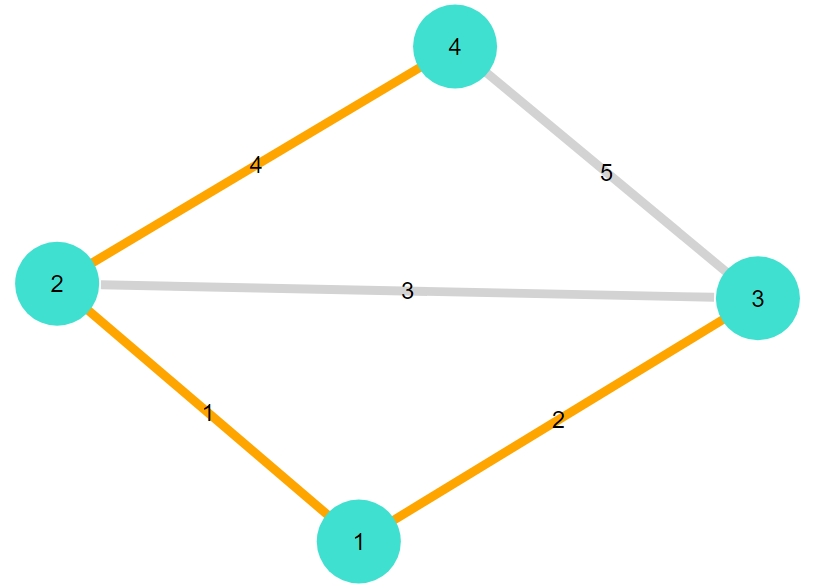
次の簡単なグラフを考えましょう。
1 2 | G1 = smallgraph(:diamond) gplot(G1, nodelabel= 1:nv(G1), edgelabel= 1:ne(G1)) |

「kruskal_mst(グラフ)」で、グラフの最小全域木がクラスカル法によって求められます。
辺をすべて取り除いたグラフに、サイクルが作られないようにひとつずつ辺を加えていく方法です。
1 | kruskal_mst(G1) |
1 2 3 4 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 2 => 4 |
結果を最短経路問題と同様にして図示してみましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | function mst_plot(g) mst = kruskal_mst(g) display(mst) colors = [colorant"lightgrey" for i in 1:ne(g)] for e in mst if isnothing(indexin([e],collect(edges(g)))[1]) != true (colors[indexin([e],collect(edges(g)))[1]] = colorant"orange" ) elseif isnothing(indexin([reverse(e)],collect(edges(g)))[1]) != true (colors[indexin([reverse(e)],collect(edges(g)))[1]] = colorant"orange" ) end end display(gplot(g, nodelabel= 1:nv(g), edgelabel= 1:ne(g), edgestrokec=colors )) end |
1 | mst_plot(G1) |
1 2 3 4 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 2 => 4 |
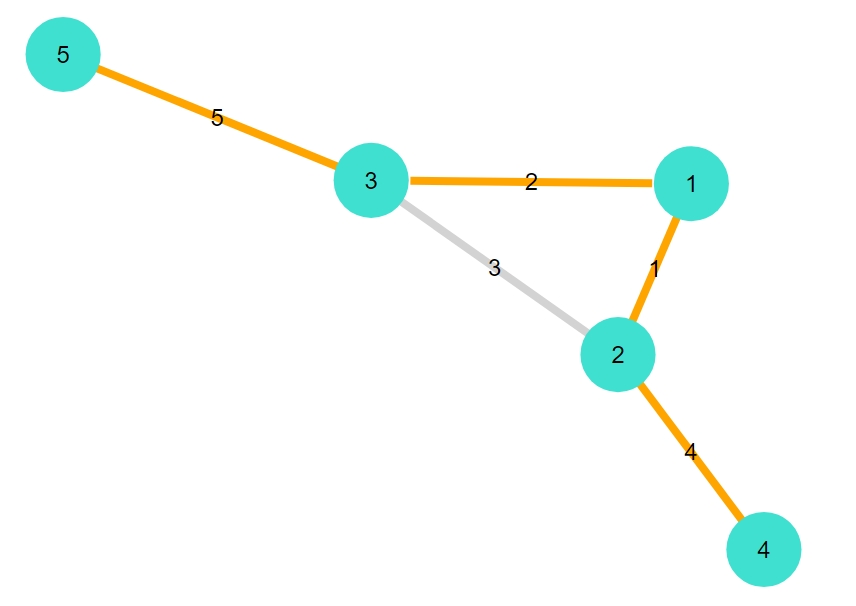
ブルグラフ(bull graph)
1 | mst_plot(smallgraph(:bull)) |
1 2 3 4 5 | 4-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 2 => 4 Edge 3 => 5 |
正多面体グラフの最小全域木
Graphs.jlでは、smallgraphという関数でプラトン立体のグラフが作れます。
1 2 3 4 5 | Platonic_solid = [:tetrahedral, :cubical, :octahedral, :dodecahedral, :icosahedral] @time for s in Platonic_solid display("$s") mst_plot(smallgraph(s)) end |
正四面体
1 2 3 4 5 | "tetrahedral" 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 1 => 4 |
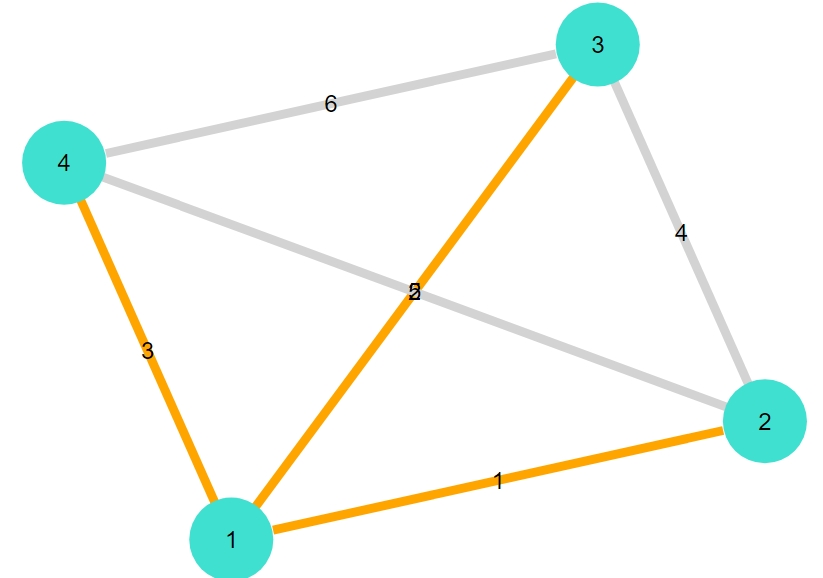
正六面体(立方体)
1 2 3 4 5 6 7 8 9 | "cubical" 7-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 4 Edge 1 => 5 Edge 2 => 3 Edge 2 => 8 Edge 3 => 7 Edge 4 => 6 |
正八面体
1 2 3 4 5 6 7 | "octahedral" 5-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 1 => 4 Edge 1 => 5 Edge 2 => 6 |
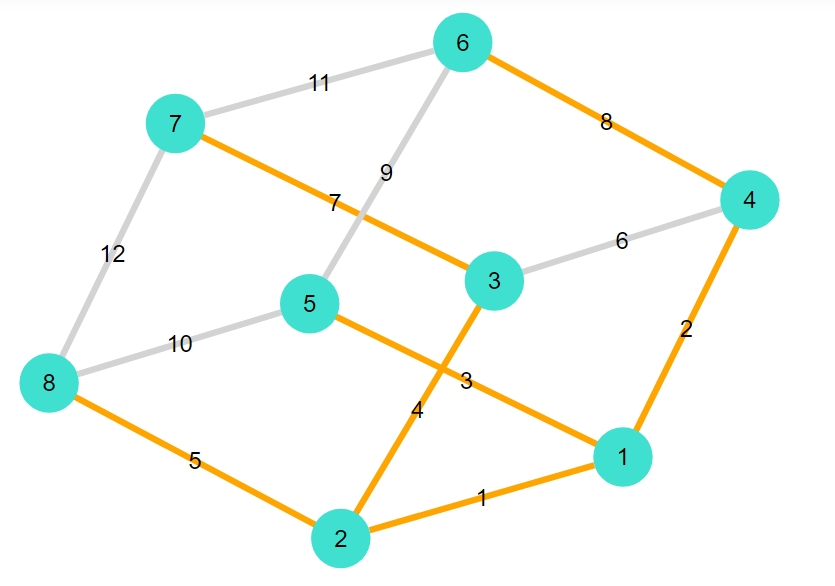
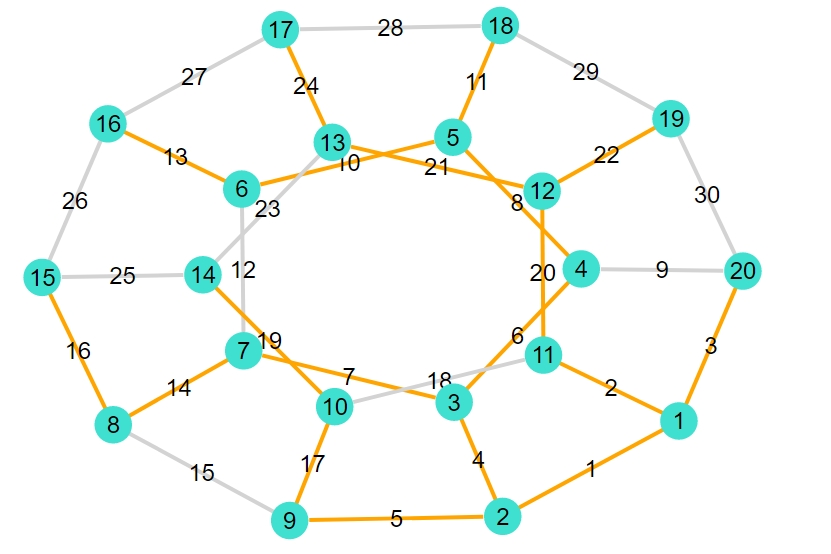
正十二面体
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | "dodecahedral" 19-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 11 Edge 1 => 20 Edge 2 => 3 Edge 2 => 9 Edge 3 => 4 Edge 3 => 7 Edge 4 => 5 Edge 5 => 6 Edge 5 => 18 Edge 6 => 16 Edge 7 => 8 Edge 8 => 15 Edge 9 => 10 Edge 10 => 14 Edge 11 => 12 Edge 12 => 13 Edge 12 => 19 Edge 13 => 17 |
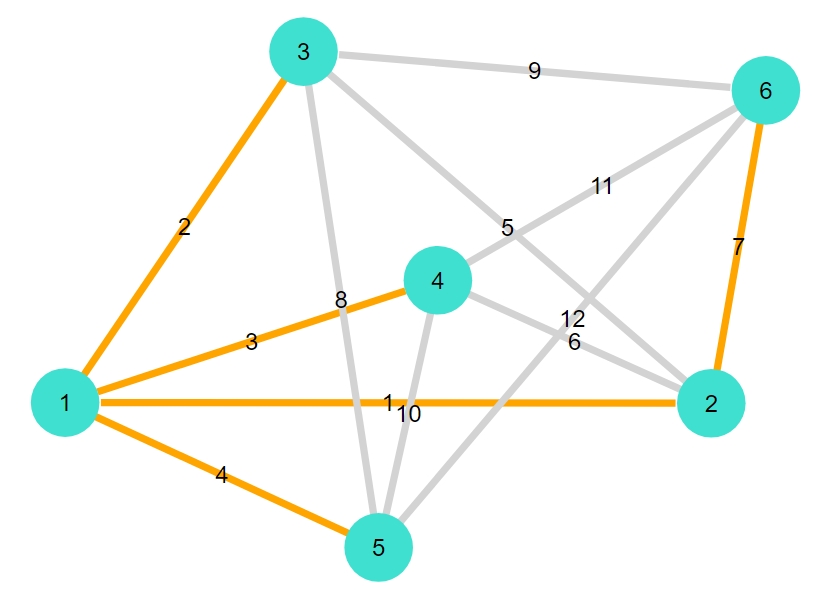
正二十面体
1 2 3 4 5 6 7 8 9 10 11 12 13 | "icosahedral" 11-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 6 Edge 1 => 8 Edge 1 => 9 Edge 1 => 12 Edge 2 => 3 Edge 2 => 7 Edge 3 => 4 Edge 3 => 10 Edge 4 => 5 Edge 4 => 11 |
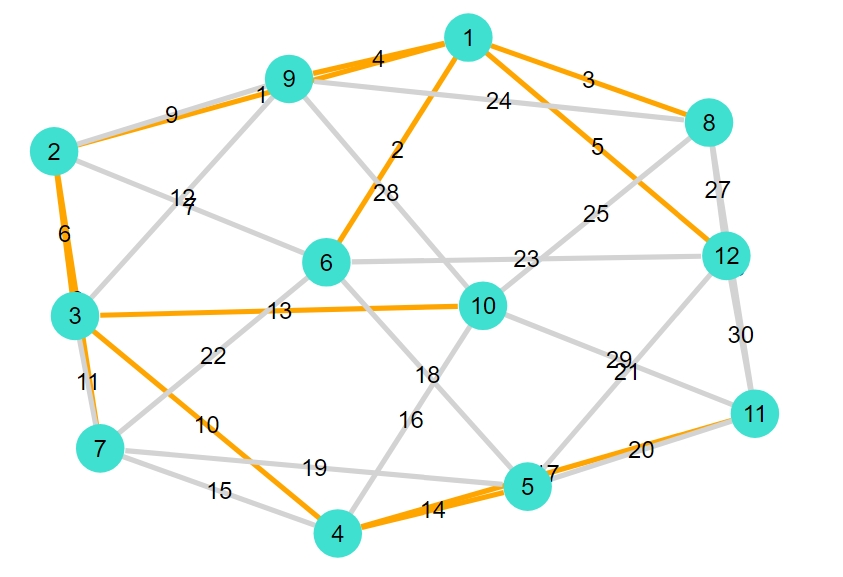
以上、Julia(Graphs)で最小全域木を求め、図示する方法を紹介してきました。
図示すると、グラフがどんな全域木を持っているかわかりやすいですね。各辺の重みが異なるケースについては、別記事で紹介予定です。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
重み付きグラフ、最小全域木の問題とは? クラスカル法による解き方
Julia(Graphs)で最短経路問題を解き、図示する方法