Julia（Graphs）で巡回セールスマン問題を解き、図示する方法

どうも、木村（@kimu3_slime）です。

今回は、Julia（Graphs）で巡回セールスマン問題を解き、図示する方法を紹介します。

前提知識：Julia（Graphs）で重みつき最短経路問題を解き、図示する方法、Julia（Graphs）でハミルトンサイクルを求め、図示する方法

準備
巡回セールスマン問題を解き、図示する方法
こちらもおすすめ

準備

Graphs, GraphPlot, Colors, Randomを使うので、持っていなければインストールしておきましょう。

using Pkg
Pkg.add("Graphs")
Pkg.add("GraphPlot")
Pkg.add("Colors")

using Pkg

Pkg.add("Graphs")

Pkg.add("GraphPlot")

Pkg.add("Colors")

準備として、以下のコードを実行しておきます。

using Graphs, GraphPlot, Colors, Random

1	using Graphs, GraphPlot, Colors, Random

巡回セールスマン問題を解き、図示する方法

巡回セールスマン問題とは

日本の47都道府県を一度ずつすべて巡りたいセールスマンがいるとして、その移動コスト（距離、時間、交通費など）を最小化するようなルートは見つけられるでしょうか。

重みつきグラフにおいて、その重さの合計を最小化するようなハミルトンサイクルを探す問題は、巡回セールスマン問題（traveling salesman problem）と呼ばれています。

ハミルトンサイクルとは、与えられたグラフのすべての頂点を一度だけ通るようなサイクル（長さ3以上の単純な閉経路）のことです。つまり、巡回セールスマン問題とは、最短ハミルトンサイクルを探す問題、と言いかえられます。

簡単な例と関数作り

まず、次のような重みベクトルを与えた無向グラフを考えましょう。

G1 = smallgraph(:diamond)
Random.seed!(2022)
weights1 = rand(1:5, 5)
gplot(G1, nodelabel= 1:nv(G1), edgelabel= weights1)

G1 = smallgraph(:diamond)

Random.seed!(2022)

weights1 = rand(1:5, 5)

gplot(G1, nodelabel= 1:nv(G1), edgelabel= weights1)

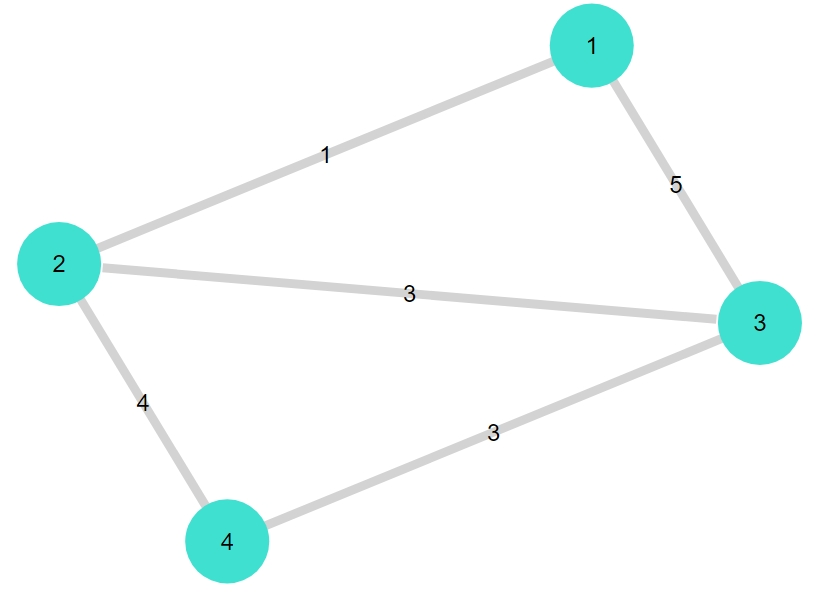
各辺に書かれている数値が、辺の重みです。今回は1から5までの整数をランダムに指定しました。「Random.seed!(2022)」によって乱数のシードを与えたので、実行結果は再現されます。

最短のハミルトンサイクルを求めるにあたって、まずグラフのハミルトンサイクルをすべて求める関数を作りましょう。

「simplecycles_limited_length」という関数で、与えられた長さ以下のサイクルがすべて求められます。そのうち長さがグラフの頂点の数に等しいものがハミルトンサイクルです。

function Hamiltonian_cycles(g)
    cycles = Vector{Int}[]
    for c in simplecycles_limited_length(g, nv(g))
        if length(c) == nv(g) && length(c) >= 3 
            push!(cycles,c)
        else
        end
    end
    return cycles
end

function Hamiltonian_cycles(g)

cycles = Vector{Int}[]

for c in simplecycles_limited_length(g, nv(g))

if length(c) == nv(g) && length(c) >= 3

push!(cycles,c)

else

end

return cycles

end

試してみると

Hamiltonian_cycles(G1)

1	Hamiltonian_cycles(G1)

2-element Vector{Vector{Int64}}:
 [1, 2, 4, 3]
 [1, 3, 4, 2]

2-element Vector{Vector{Int64}}:

[1, 2, 4, 3]

[1, 3, 4, 2]

確かにハミルトンサイクルたちが求められています。これらは向きが異なるだけで実質同じサイクルですが、一般にはたくさんのハミルトンサイクルが得られるでしょう。

得られたハミルトンサイクルから、最短のものを探しましょう。そのためにまず、サイクルの重みの合計を求める関数を作ります。

重みベクトルを距離行列に変換して、距離行列の情報を使って与えられたサイクルの重みを求めます。

function distance_matrix(g, weights)
    D = zeros(Int,(nv(g),nv(g)))
    for i in 1:length(weights)
        D[collect(edges(g))[i].src,collect(edges(g))[i].dst] = weights[i]
        D[collect(edges(g))[i].dst,collect(edges(g))[i].src] = weights[i]
    end
    return D
end

function distance_matrix(g, weights)

D = zeros(Int,(nv(g),nv(g)))

for i in 1:length(weights)

D[collect(edges(g))[i].src,collect(edges(g))[i].dst] = weights[i]

D[collect(edges(g))[i].dst,collect(edges(g))[i].src] = weights[i]

end

return D

end

function weight_sum_cycle( cycle , g, weights)
    weight_sum = 0
    for i in 1:(length(cycle)-1)
        weight_sum += distance_matrix(g, weights)[cycle[i],cycle[i+1]]
    end
    weight_sum += distance_matrix(g, weights)[cycle[length(cycle)],cycle[1]]
    return weight_sum
end

function weight_sum_cycle( cycle , g, weights)

weight_sum = 0

for i in 1:(length(cycle)-1)

weight_sum += distance_matrix(g, weights)[cycle[i],cycle[i+1]]

end

weight_sum += distance_matrix(g, weights)[cycle[length(cycle)],cycle[1]]

return weight_sum

end

これで与えられたサイクルの重み合計が計算できるようになりました。

weight_sum_cycle(Hamiltonian_cycles(G1)[1], G1, weights1)

1	weight_sum_cycle(Hamiltonian_cycles(G1)[1], G1, weights1)

13

これを使って、最短ハミルトンサイクルとその重み合計を求める関数を作ります。

function shortest_Hamiltonian_cycle(g, weights)
    cycles = Hamiltonian_cycles(g)
    cycles_weight = Float64[]
    for cycle in cycles
        push!(cycles_weight, weight_sum_cycle(cycle,g,weights))
    end
    return [cycles[argmin(cycles_weight)],cycles_weight[argmin(cycles_weight)] ]
end

function shortest_Hamiltonian_cycle(g, weights)

cycles = Hamiltonian_cycles(g)

cycles_weight = Float64[]

for cycle in cycles

push!(cycles_weight, weight_sum_cycle(cycle,g,weights))

end

return [cycles[argmin(cycles_weight)],cycles_weight[argmin(cycles_weight)] ]

end

「cycles_weight」として、各サイクルの重みを集めた配列を作っています。そして「argmin」でその配列の最小値を取る変数を取り出して、結果を返しました。

shortest_Hamiltonian_cycle(G1,weights1)

1	shortest_Hamiltonian_cycle(G1,weights1)

2-element Vector{Any}:
   [1, 2, 4, 3]
 13.0

2-element Vector{Any}:

[1, 2, 4, 3]

13.0

グラフと重みが与えられたとき、最短ハミルトンサイクルとその重み合計が求められます。

さらに、結果を最短経路問題、ハミルトンサイクルを求める問題と同様にして図示してみましょう。

function shortest_Hamiltonian_cycle_plot(g, weights)    
    if Hamiltonian_cycles(g) != []
        cycle = shortest_Hamiltonian_cycle(g,weights)[1]
        weight_sum =shortest_Hamiltonian_cycle(g,weights)[2]
        display("最短ハミルトンサイクル：$cycle")
        display("重み合計：$weight_sum")

        GE = SimpleGraph(nv(g))
        for i in 1:length(cycle)-1
            add_edge!(GE, cycle[i], cycle[i+1])
        end
        add_edge!(GE, cycle[length(cycle)], cycle[1])

        colors = [colorant"lightgrey" for i in  1:ne(g)]
        for e in collect(edges(GE))
            if isnothing(indexin([e],collect(edges(g)))[1]) != true
                (colors[indexin([e],collect(edges(g)))[1]]
                    = colorant"orange" )
            elseif isnothing(indexin([reverse(e)],collect(edges(g)))[1]) != true
                (colors[indexin([reverse(e)],collect(edges(g)))[1]]
                    = colorant"orange" )
            end
        end
        display(gplot(g, nodelabel= 1:nv(g), edgelabel= weights, edgestrokec=colors))
    else
        println("ハミルトンサイクルは存在しない")
    end
end

function shortest_Hamiltonian_cycle_plot(g, weights)

if Hamiltonian_cycles(g) != []

cycle = shortest_Hamiltonian_cycle(g,weights)[1]

weight_sum =shortest_Hamiltonian_cycle(g,weights)[2]

display("最短ハミルトンサイクル：$cycle")

display("重み合計：$weight_sum")

GE = SimpleGraph(nv(g))

for i in 1:length(cycle)-1

add_edge!(GE, cycle[i], cycle[i+1])

end

add_edge!(GE, cycle[length(cycle)], cycle[1])

colors = [colorant"lightgrey" for i in 1:ne(g)]

for e in collect(edges(GE))

if isnothing(indexin([e],collect(edges(g)))[1]) != true

(colors[indexin([e],collect(edges(g)))[1]]

= colorant"orange" )

elseif isnothing(indexin([reverse(e)],collect(edges(g)))[1]) != true

(colors[indexin([reverse(e)],collect(edges(g)))[1]]

= colorant"orange" )

end

display(gplot(g, nodelabel= 1:nv(g), edgelabel= weights, edgestrokec=colors))

else

println("ハミルトンサイクルは存在しない")

end

if文を使い、ハミルトンサイクルが存在するかどうかによって、表示結果を変えています。

shortest_Hamiltonian_cycle_plot(G1, weights1)

1	shortest_Hamiltonian_cycle_plot(G1, weights1)

"最短ハミルトンサイクル：[1, 2, 4, 3]"
"重み合計：13.0"

1 2	"最短ハミルトンサイクル：[1, 2, 4, 3]" "重み合計：13.0"

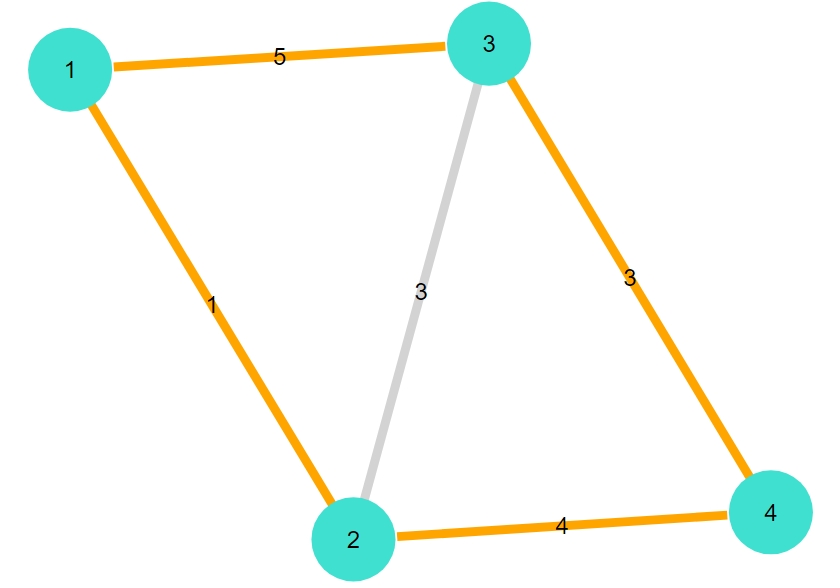
これで巡回セールスマン問題の結果が、ひと目でわかるようになりました。

ハミルトンサイクルが存在しない例

G2 = smallgraph(:bull)
Random.seed!(2022)
weights2 = rand(1:5, ne(G2))

G2 = smallgraph(:bull)

Random.seed!(2022)

weights2 = rand(1:5, ne(G2))

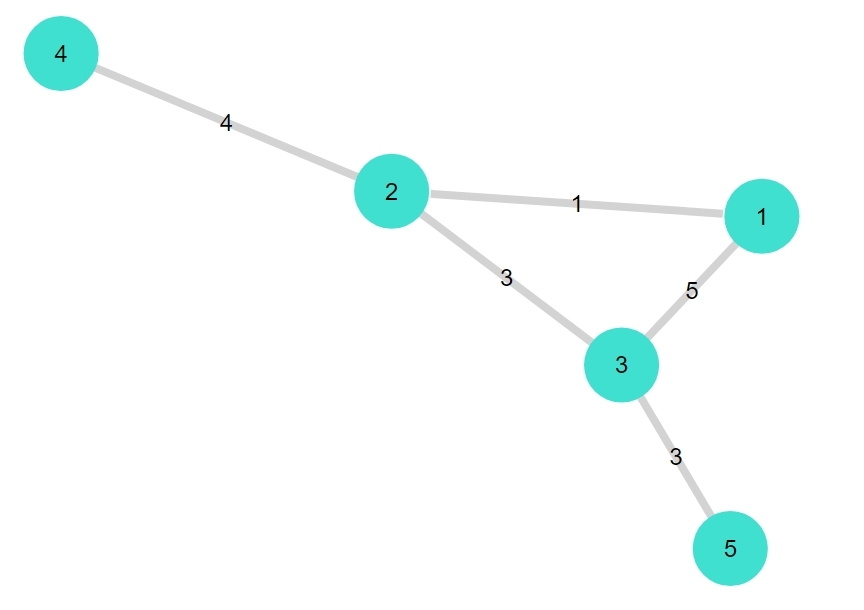
このグラフ（bull graph）は、ハミルトンサイクルを持ちません。

shortest_Hamiltonian_cycle_plot(G2, weights2)

1	shortest_Hamiltonian_cycle_plot(G2, weights2)

ハミルトンサイクルは存在しない

1	ハミルトンサイクルは存在しない

きちんと適切な結果が表示されています。

正多面体グラフの最短ハミルトンサイクル

プラトン立体（正多面体）のグラフは、複数のハミルトンサイクルを持っています。各辺にランダムな重みを割り当て、その最短ハミルトンサイクルを求めてみましょう。

Graphs.jlでは、smallgraphという関数でプラトン立体のグラフが作れます。

Random.seed!(2022)
Platonic_solid = [:tetrahedral, :cubical, :octahedral, :dodecahedral, :icosahedral]
@time for s in Platonic_solid
    display("$s")
    shortest_Hamiltonian_cycle_plot(smallgraph(s),rand(1:5, ne(smallgraph(s))) )
end

Random.seed!(2022)

Platonic_solid = [:tetrahedral, :cubical, :octahedral, :dodecahedral, :icosahedral]

@time for s in Platonic_solid

display("$s")

shortest_Hamiltonian_cycle_plot(smallgraph(s),rand(1:5, ne(smallgraph(s))) )

end

正四面体

"tetrahedral"
"最短ハミルトンサイクル：[1, 2, 3, 4]"
"重み合計：12.0"

"tetrahedral"

"最短ハミルトンサイクル：[1, 2, 3, 4]"

"重み合計：12.0"

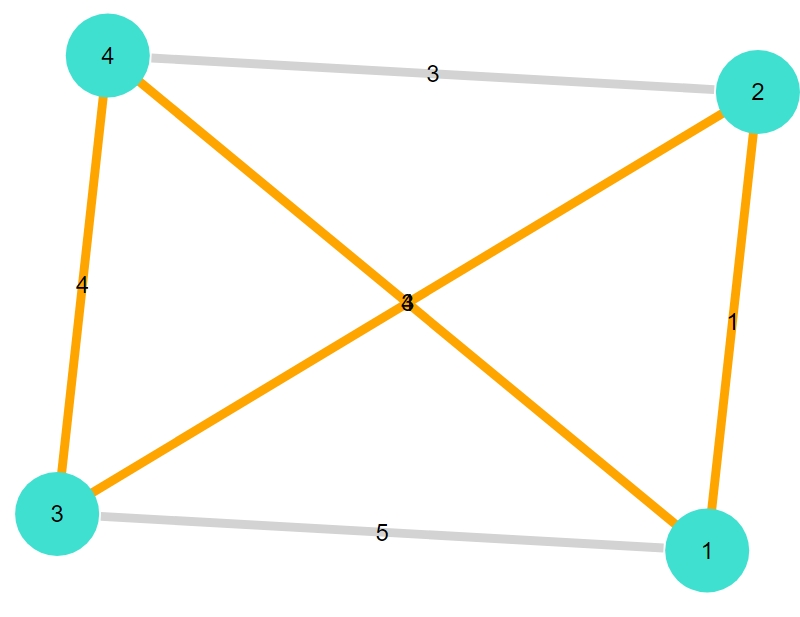
正六面体（立方体）

"cubical"
"最短ハミルトンサイクル：[1, 2, 3, 7, 8, 5, 6, 4]"
"重み合計：24.0"

"cubical"

"最短ハミルトンサイクル：[1, 2, 3, 7, 8, 5, 6, 4]"

"重み合計：24.0"

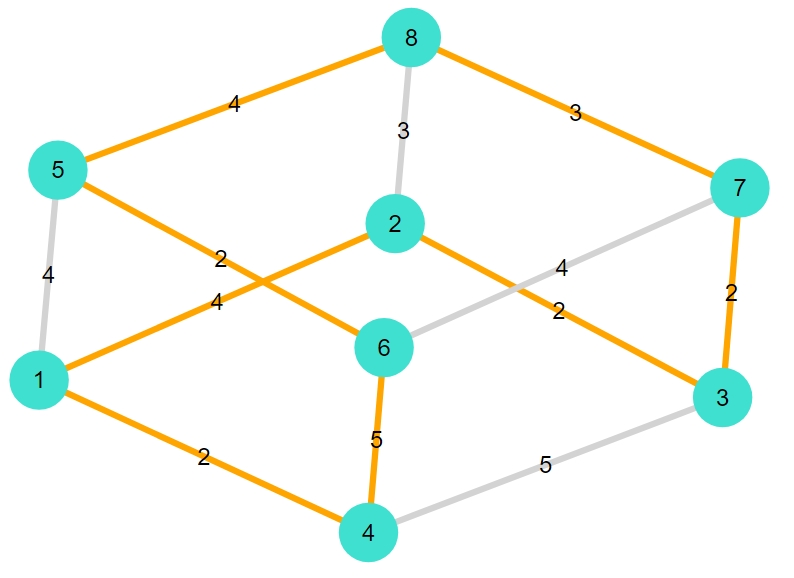
正八面体

"octahedral"
"最短ハミルトンサイクル：[1, 3, 2, 6, 4, 5]"
"重み合計：14.0"

"octahedral"

"最短ハミルトンサイクル：[1, 3, 2, 6, 4, 5]"

"重み合計：14.0"

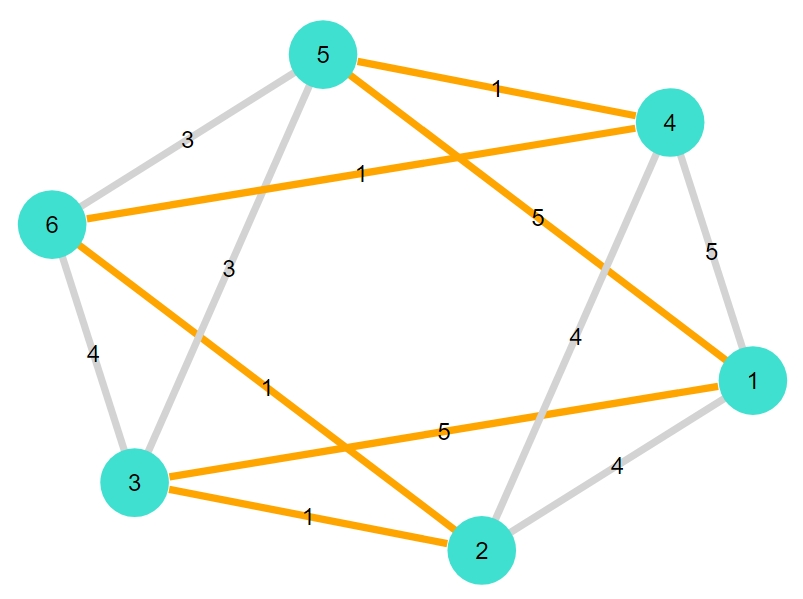
正十二面体

"dodecahedral"
"最短ハミルトンサイクル：[1, 2, 9, 10, 14, 13, 17, 18, 5, 6, 16, 15, 8, 7, 3, 4, 20, 19, 12, 11]"
"重み合計：47.0"

"dodecahedral"

"最短ハミルトンサイクル：[1, 2, 9, 10, 14, 13, 17, 18, 5, 6, 16, 15, 8, 7, 3, 4, 20, 19, 12, 11]"

"重み合計：47.0"

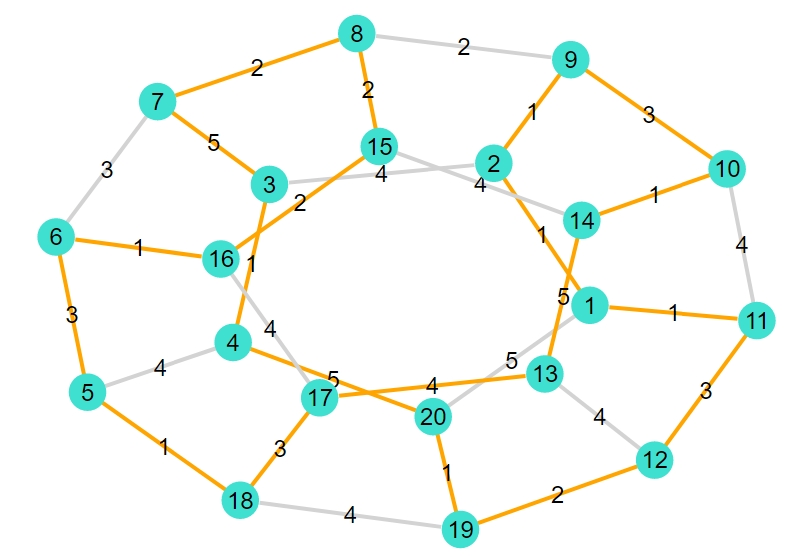
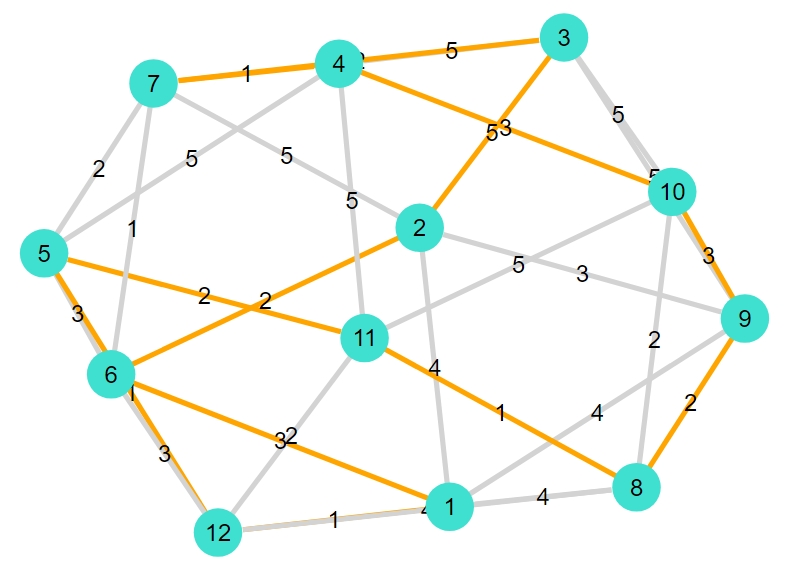
正二十面体

"icosahedral"
"最短ハミルトンサイクル：[1, 6, 2, 3, 7, 4, 10, 9, 8, 11, 5, 12]"
"重み合計：26.0"

"icosahedral"

"最短ハミルトンサイクル：[1, 6, 2, 3, 7, 4, 10, 9, 8, 11, 5, 12]"

"重み合計：26.0"

以上、Julia（Graphs）で巡回セールスマン問題を解き、図示する方法を紹介してきました。

巡回セールスマン問題は、計算量理論ではNP困難であることが知られていて、原理的に計算時間がかかります。

ただし、今回見たような小さなサイズの問題ならば、正多面体グラフの最短ハミルトンサイクルをすべて求めて表示するのに8秒程度で済んでいます。グラフと重みを与えるだけで計算できるので、試してみてはいかがでしょうか。

木村すらいむ（@kimu3_slime）でした。ではでは。

1から始める Juliaプログラミング

posted with AmaQuick at 2021.10.29

進藤裕之(著), 佐藤建太(著)
コロナ社 (2020-03-26T00:00:01Z)

￥7,353 (コレクター商品)

Amazon.co.jpで詳細を見る

こちらもおすすめ

グラフ理論における経路、連結性とは？

Julia（Graphs）で最短経路問題を解き、図示する方法

Julia（Graphs）でハミルトンサイクルを求め、図示する方法

Julia（Graphs）で重みつき最短経路問題を解き、図示する方法