どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)で重みつき最短経路問題を解き、図示する方法を紹介します。
前提知識:Julia(Graphs)で最短経路問題を解き、図示する方法
準備
Graphs, GraphPlot,Colors, Randomを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors, Random |
重み付き最短経路問題を解き、図示する方法
最短経路問題(shortest path problem)は、与えられたグラフの2つの頂点間の距離を最も短くするような経路を探す問題です。
特に、重み付き最短経路問題(weighted shortest path problem)は、各辺ごとに異なった重み(長さや移動時間)を与えて、「経路の重み合計を最小化する」意味での最短経路を探す問題です。
重み付き最短経路の求め方
より具体的に、次のグラフの重み付き最短経路を探してみましょう。まずは、辺の番号をそのまま図示します。
1 2 | G1 = smallgraph(:diamond) gplot(G1, nodelabel= 1:nv(G1), edgelabel= 1:ne(G1)) |
1 | {4, 5} undirected simple Int64 graph |
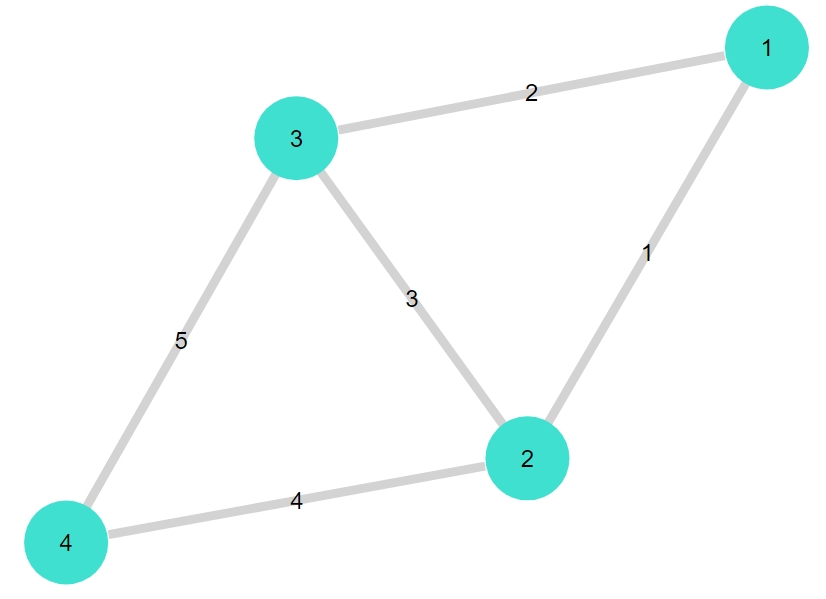
この時点では、グラフは頂点と辺の情報のみを持ち、重みの情報がありません。
1 | collect(edges(G1)) |
1 2 3 4 5 6 | 5-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 2 => 3 Edge 2 => 4 Edge 3 => 4 |
グラフが持つ各辺に対して、ベクトルとして重みを定義し(重みベクトル weight vector)、それを図示してみましょう。
今回の重みの値としては、1から5の値をランダムに指定します。結果が再現されるように、「Random.seed!(2022)」で乱数のシードを指定しました。
1 2 | Random.seed!(2022) weights = rand(1:5, 5) |
1 2 3 4 5 6 | 5-element Vector{Int64}: 1 5 3 4 3 |
「Edge 1 => 2」の重みは1、「Edge 1 => 3」の重みは5、といった対応関係です。
このベクトルを使ってグラフを描けば、各辺の重みがどうなっているかわかりやすいです。
1 | gplot(G1, nodelabel= 1:nv(G1), edgelabel= weights) |
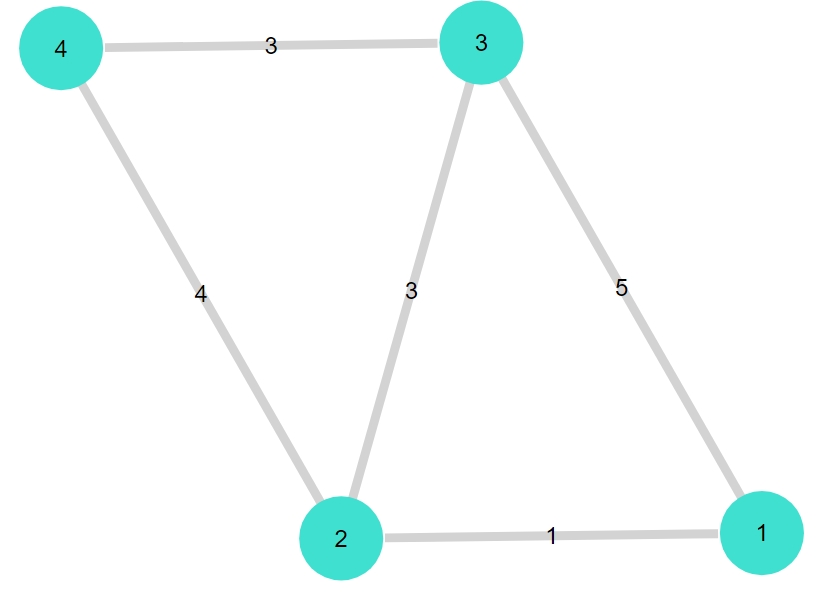
重みを考慮した上で最短経路を探すには「a_star(グラフ, 始点,終点,距離行列)」という関数を用います。これはA*探索アルゴリズム(A* search algorithm)と呼ばれる方法で、最短経路を求めています。
ここで距離行列(distance matrix)\(D=(d_{ij})\)とは、
\[d_{ij}= \begin{cases}w_{ij}(始点i,終点jの辺の重み) & (始点i,終点jの辺がある )\\0 & (始点i,終点jの辺がない)\end{cases}\]
として定義される行列です。今回は向きのないグラフ(無向グラフ)を考えているので、「始点i,終点jの辺の重み」と「始点j,終点iの辺の重み」は等しく、対称行列として与える必要があります。
まず、さきほど定義した重みベクトルを、距離行列に変換しましょう。
1 2 3 4 5 6 | D1 = zeros(Int,(nv(G1),nv(G1))) for i in 1:length(weights) D1[collect(edges(G1))[i].src,collect(edges(G1))[i].dst] = weights[i] D1[collect(edges(G1))[i].dst,collect(edges(G1))[i].src] = weights[i] end D1 |
1 2 3 4 5 | 4×4 Matrix{Int64}: 0 1 5 0 1 0 3 4 5 3 0 3 0 4 3 0 |
「collect(edges(G1))[i].src」はi番目の辺の始点(source)、「collect(edges(G1))[i].dst」は終点(destination)です。行列\(D\)の辺に対応した成分に重みベクトルの値を代入しています。
始点と終点を入れ替えて同じ値を代入することで、向きのないグラフとして辺に重さを指定しました。
結果は確かに対応する部分が重みの値を持つ行列で、対称行列となっています。
こうして得た距離行列を使って最短経路を探してみます。
1 | a_star(G1, 1,4,D1) |
1 2 3 | 2-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 2 => 4 |

他の経路、例えば「Edge 1 => 3, Edge 3 => 4」の重みの合計はより大きいのく、確かに最短経路が求まっていますね。
最短経路の重みの合計を求める関数「path_weight_sum」を作ってみましょう。
1 2 3 4 5 6 7 8 | function path_weight_sum(g,a,b,D) path = a_star(g, a, b, D) weight_sum = 0 for p in path weight_sum += D[p.src, p.dst] end return weight_sum end |
1 | path_weight_sum (generic function with 1 method) |
最短経路を求め、その経路の辺ごとに重みの値を足していった結果を返します。
1 | path_weight_sum(G1,1,4,D1) |
1 | 5 |
他の頂点でも、最短経路とその重み合計を求められます。
1 2 | a_star(G1, 1,3,D1) path_weight_sum(G1,1,3,D1) |
1 2 3 4 | 2-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 2 => 3 4 |
1 2 | a_star(G1, 2,4,D1) path_weight_sum(G1,2,4,D1) |
1 2 3 | 1-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 2 => 4 4 |
一般化
さて、今までやってきた計算を一般化してみましょう。
まず、重みベクトルを距離行列に変換する関数「distance_matrix」を作ります。
1 2 3 4 5 6 7 8 | function distance_matrix(g, weights) D = zeros(Int,(nv(g),nv(g))) for i in 1:length(weights) D[collect(edges(g))[i].src,collect(edges(g))[i].dst] = weights[i] D[collect(edges(g))[i].dst,collect(edges(g))[i].src] = weights[i] end return D end |
1 | distance_matrix(G1, weights) |
1 2 3 4 5 | 4×4 Matrix{Int64}: 0 1 5 0 1 0 3 4 5 3 0 3 0 4 3 0 |
確かにさきほどと同じ結果が得られます。
さらに、最短経路と重みの合計を求め、最短経路を図示する関数「shortest_path_plot」を作りましょう。
最短経路の色づけについては、重みの等しい最短経路問題で作った関数と同じです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | function shortest_path_plot(g,a,b,weights) D = distance_matrix(g, weights) shortest_path = a_star(g, a,b, D) display(shortest_path) println("重み合計:",path_weight_sum(g,a,b,D)) colors = [colorant"lightgrey" for i in 1:ne(g)] for e in shortest_path if isnothing(indexin([e],collect(edges(g)))[1]) != true (colors[indexin([e],collect(edges(g)))[1]] = colorant"orange" ) elseif isnothing(indexin([reverse(e)],collect(edges(g)))[1]) != true (colors[indexin([reverse(e)],collect(edges(g)))[1]] = colorant"orange" ) end end gplot(g, nodelabel= 1:nv(g), edgelabel= weights, edgestrokec=colors ) end |
1 | shortest_path_plot(G1,1,4,weights) |
1 2 3 4 | 2-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 2 => 4 重み合計:5 |
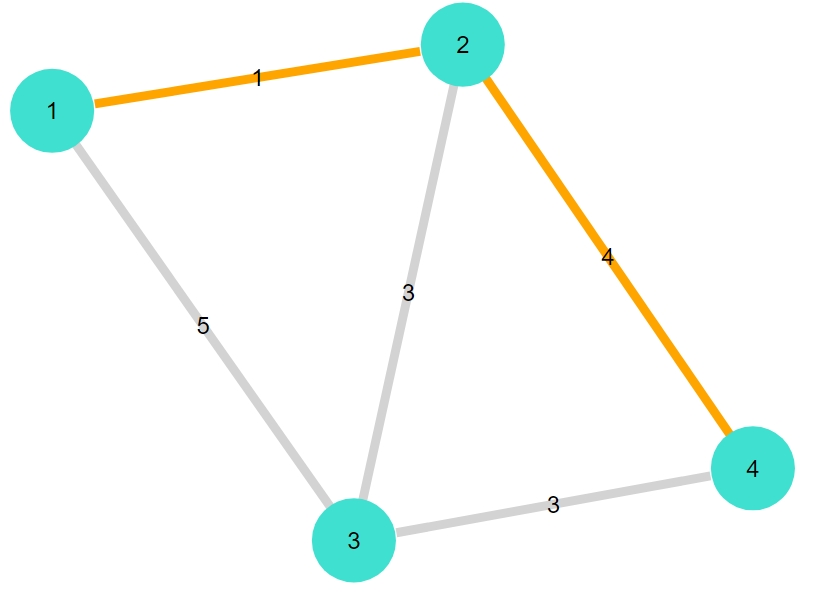
ひと目で結果がわかるようになりました。
別のグラフ、別の重みで試してみましょう。
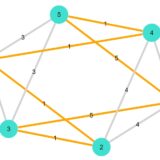
1 2 3 4 5 | G2 = smallgraph(:dodecahedral) Random.seed!(2022) weights2 = rand(1:5, ne(G2)) shortest_path_plot(G2,1,4,weights2) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | {20, 30} undirected simple Int64 graph 30-element Vector{Int64}: 1 5 3 4 3 4 3 5 1 1 4 3 5 ⋮ 3 5 2 5 2 4 4 3 4 4 2 4 |
1 2 3 4 | 2-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 20 Edge 20 => 4 重み合計:4 |
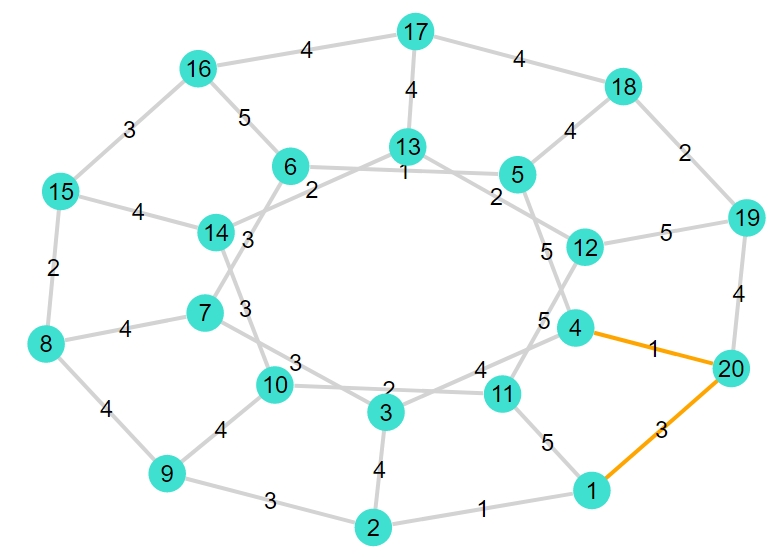
各辺の重み、最短経路、最短経路の重みがひと目でわかります。
別の頂点について試してみましょう。
1 | shortest_path_plot(G2,1,15,weights2) |
1 2 3 4 5 6 | 4-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 2 => 9 Edge 9 => 8 Edge 8 => 15 重み合計:10 |
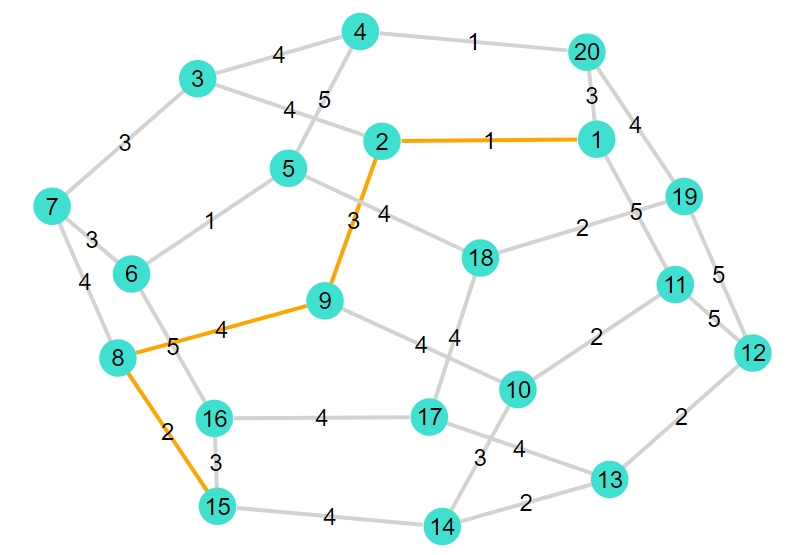
以上、Julia(Graphs)で重みつき最短経路問題を解き、図示する方法を紹介してきました。
各辺が異なる重みを持つケースでは、手計算で最短経路を求めるのがより難しくなるので、コンピュータで求められると嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法
重み付きグラフ、最小全域木の問題とは? クラスカル法による解き方
Julia(Graphs)で最短経路問題を解き、図示する方法