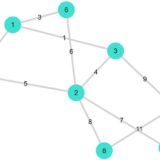
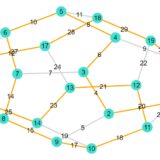
どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)で最短経路問題を解き、図示する方法を紹介します。
前提知識:Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法
準備
Graphs, GraphPlot,Colorsを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") Pkg.add("Colors") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot, Colors |
最短経路問題を解き、図示する方法
最短経路問題(shortest path problem)は、与えられたグラフの2つの頂点間の距離を最も短くするような経路を探す問題です。
一般的には、各辺ごとに異なった重み(長さ、移動時間)を考えることができます。ただし今回は、どの辺も等しい重み(1)を持つケースを考えます。
より具体的に、次のグラフの最短経路を探してみましょう。
1 2 | G1 = smallgraph(:diamond) gplot(G1, nodelabel= 1:nv(G1), edgelabel= 1:ne(G1)) |
1 | {4, 5} undirected simple Int64 graph |
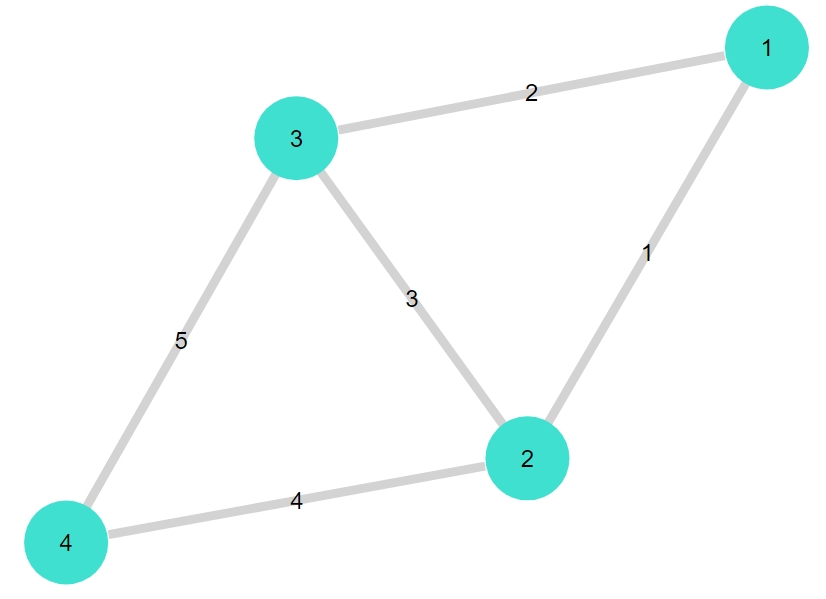
「a_star(グラフ, 始点,終点)」で、グラフの始点から終点までの経路を求めてくれます。
これはA*探索アルゴリズム(A* search algorithm)と呼ばれる方法で、ダイクストラ法(Dijkstra’s algorithm)を一般化したものとなっています。評価関数をうまく選んで、その情報を使いながら始点から経路の木をひとつずつ伸ばしていく探索法です。
1 | a_star(G1, 1,4) |
1 2 3 | 2-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 2 => 4 |
経路は辺を成分とするベクトルとして返ってきます。頂点1と4を結ぶ最短経路は、1から2、2から4へと進むもの、ということです。
length関数を使えば、そのベクトルの成分数、つまり最短経路の長さが求められます。
1 | length(a_star(G1, 1,4)) |
1 | 2 |
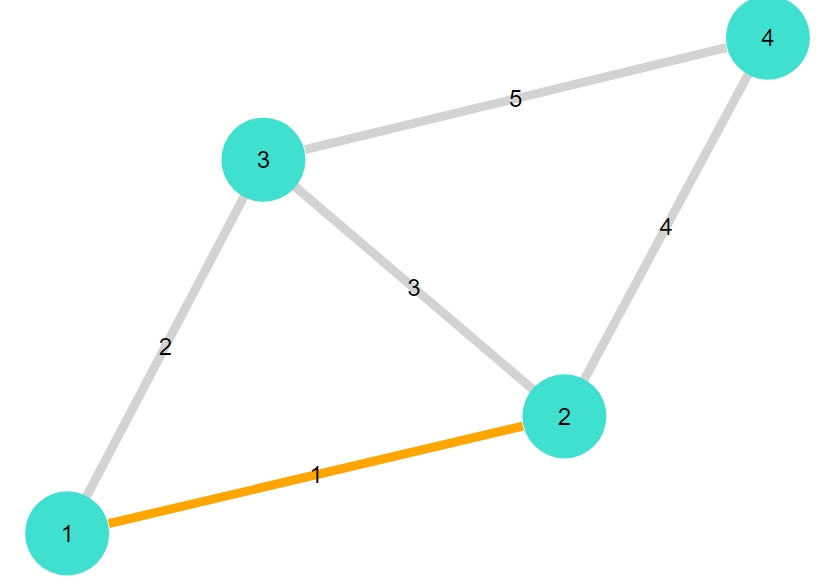
この結果をわかりやすくするために、図示してみましょう。
グラフをプロットする関数gplotは、edgestrokecというオプションで辺に色を指定できます。
1 2 3 4 5 6 7 8 | colors = [colorant"lightgrey" for i in 1:ne(G1)] for e in a_star(G1, 1,4) (colors[indexin([e],collect(edges(G1)))[1]] = colorant"orange" ) end colors gplot(G1,nodelabel= 1:nv(G1), edgelabel= 1:ne(G1), edgestrokec=colors ) |
色の指定は配列で行うことができ、例えば4番の辺にオレンジ色をつけたいなら、「colors[4]=colorant”orange”」とします。
上のコードでは、まずすべての辺に対して通常色を与える配列colorを作ります。そして、最短経路に含まれるすべての辺に対し、indexinでその辺が何番目なのかを取り出し、その番号のcolorをオレンジ色にしました。

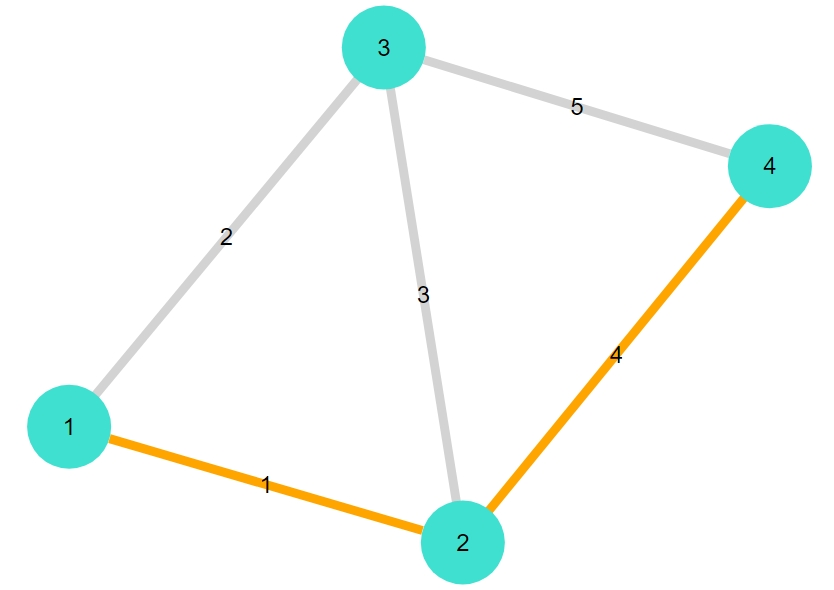
これで最短経路がひと目でわかるようになりましたね。
以上の結果を一般化して、最短経路とその長さを求め、それをプロットする関数を作りましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | function shortest_path_plot(g,a,b) display(a_star(g, a,b)) println("経路の長さ:",length(a_star(g, a,b))) colors = [colorant"lightgrey" for i in 1:ne(g)] for e in a_star(g, a,b) if isnothing(indexin([e],collect(edges(g)))[1]) != true (colors[indexin([e],collect(edges(g)))[1]] = colorant"orange" ) elseif isnothing(indexin([reverse(e)],collect(edges(g)))[1]) != true (colors[indexin([reverse(e)],collect(edges(g)))[1]] = colorant"orange" ) end end gplot(g, nodelabel= 1:nv(g), edgelabel= 1:ne(g), edgestrokec=colors) end |
色をつける部分でif文による分岐が加わっています。それは次の理由です。
1 | collect(edges(G1)) |
1 2 3 4 5 6 | 5-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 2 Edge 1 => 3 Edge 2 => 3 Edge 2 => 4 Edge 3 => 4 |
グラフの辺としては「Edge 1 => 2」があるのですが、indexinで番号を取り出すときに、(無向グラフであるにもかかわらず)「Edge 2 => 1」は存在しないとなってしまうためです。
1 | print(indexin([a_star(G1, 2,1)[1]],collect(edges(G1)))[1]) |
1 | nothing |
(「has_edge(G1,2,1)」という関数を使えば、この辺はグラフに確かに存在することがわかりますが、この関数では辺の番号が取り出せません。)
そこで、if文で分岐を加え、逆向きの辺を得る「reverse(辺)」を合わせて色の追加をすることにしました。もう少し簡単な記述方法があるかもしれません。
これを使えば、頂点を与える順序に関わらず、最短経路が求められます。
1 | shortest_path_plot(G1,2,1) |
1 2 3 | 1-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 2 => 1 経路の長さ:1 |
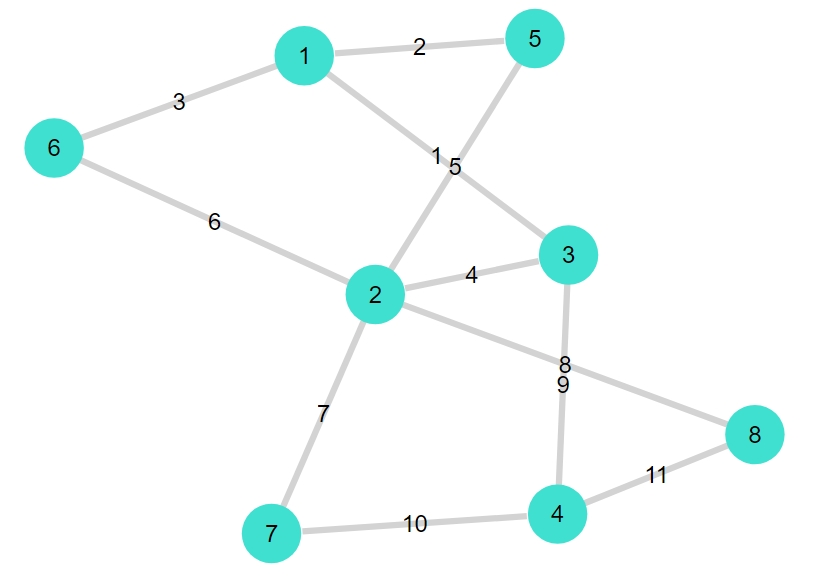
ケーニヒスベルクの橋のグラフで、最短経路を求めてみます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | G2 = smallgraph(:diamond) add_vertices!(G2,4) add_edge!(G2 , 1, 5) add_edge!(G2 , 1, 6) add_edge!(G2 , 2, 5) add_edge!(G2 , 2, 6) add_edge!(G2 , 2, 7) add_edge!(G2 , 2, 8) add_edge!(G2 , 4, 7) add_edge!(G2 , 4, 8) rem_edge!(G2 , 1, 2) rem_edge!(G2 , 2, 4) G2 gplot(G2,nodelabel= 1:nv(G2), edgelabel= 1:ne(G2)) |
1 | {8, 11} undirected simple Int64 graph |
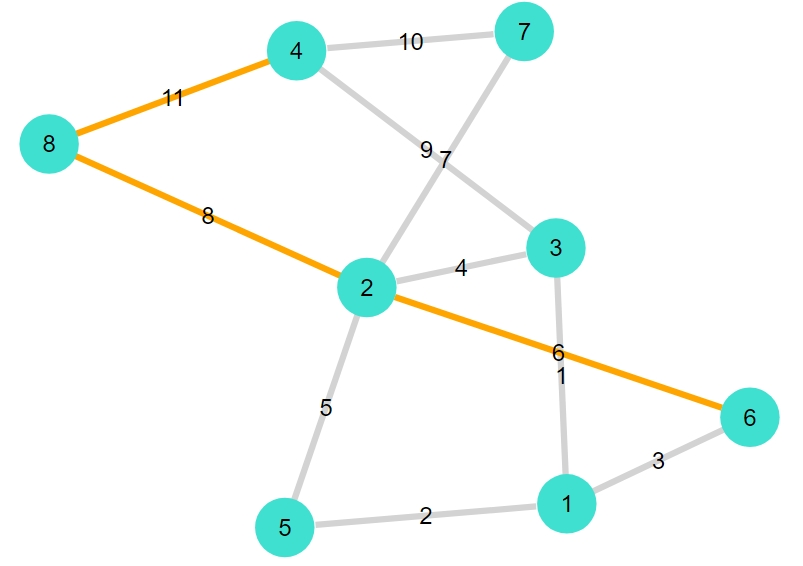
1 | shortest_path_plot(G2,1,8) |
1 2 3 4 5 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 1 => 3 Edge 3 => 2 Edge 2 => 8 経路の長さ:3 |

1 | shortest_path_plot(G2,6,4) |
1 2 3 4 5 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 6 => 2 Edge 2 => 8 Edge 8 => 4 経路の長さ:3 |
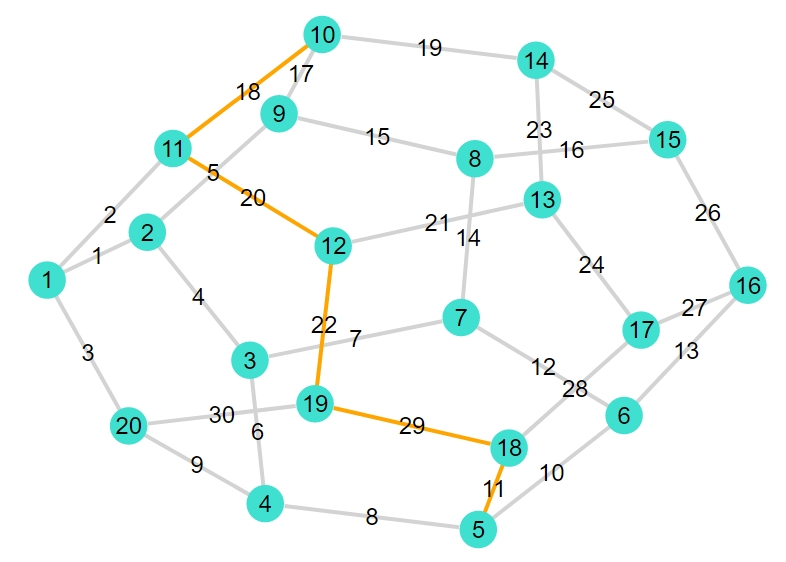
もう少しサイズの大きなグラフとして、正20面体グラフにおける最短経路を求めてみましょう。
1 2 | G3 = smallgraph(:dodecahedral) gplot(G3,nodelabel= 1:nv(G3), edgelabel= 1:ne(G3)) |
1 | {20, 30} undirected simple Int64 graph |

1 | shortest_path_plot(G3,5,10) |
1 2 3 4 5 6 7 | 5-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 5 => 18 Edge 18 => 19 Edge 19 => 12 Edge 12 => 11 Edge 11 => 10 経路の長さ:5 |
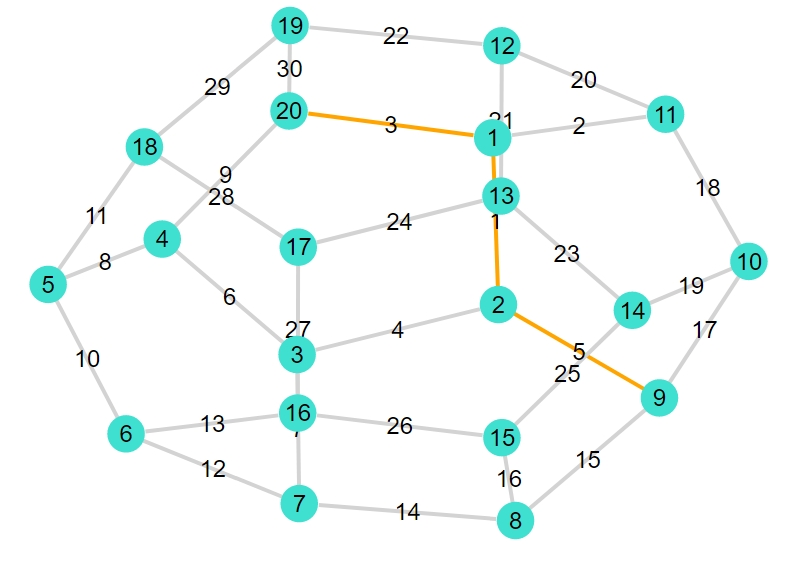
1 | shortest_path_plot(G3,20,9) |
1 2 3 4 5 | 3-element Vector{Graphs.SimpleGraphs.SimpleEdge{Int64}}: Edge 20 => 1 Edge 1 => 2 Edge 2 => 9 経路の長さ:3 |
以上、Julia(Graphs)で最短経路問題を解き、図示する方法を紹介してきました。
頂点数や辺の数が増えるほど、最短経路を手計算で求めるのは難しくなりますが、コンピュータだと簡単に早く解けるので嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法