どうも、木村(@kimu3_slime)です。
今回は、Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法を紹介します。
前提知識:グラフ理論入門:グラフとは、グラフの同型
準備
Graphs, GraphPlotを使うので、持っていなければインストールしておきましょう。
1 2 3 | using Pkg Pkg.add("Graphs") Pkg.add("GraphPlot") |
準備として、以下のコードを実行しておきます。
1 | using Graphs, GraphPlot |
グラフの作成とプロット
「Graph(頂点数)」で、指定された個数の頂点を持つグラフが作成できます。
1 | G1 = Graph(4) |
1 | {4, 0} undirected simple Int64 graph |
頂点数4、辺の数0の(向きのない=無向)グラフです。
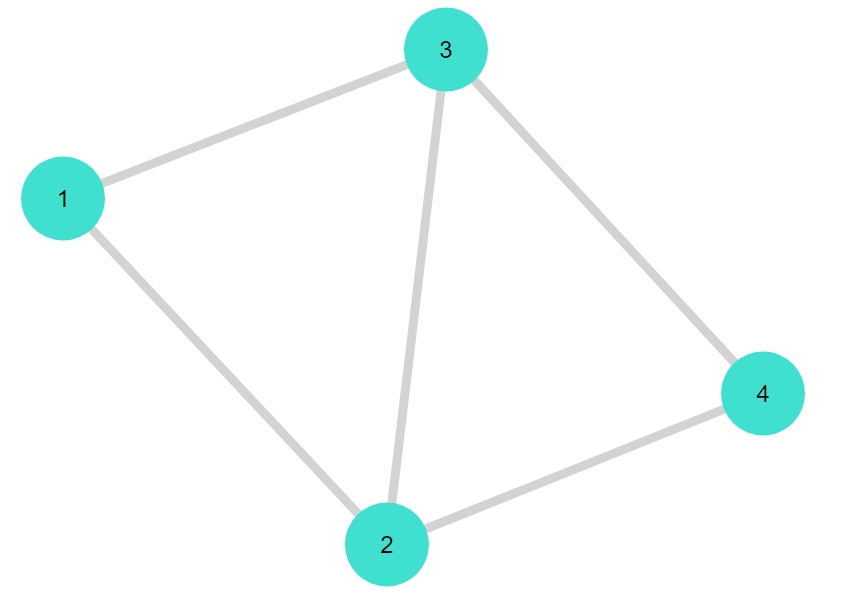
この時点では頂点のみで、頂点の間に辺はありません。辺は「add_edge!(グラフ, 頂点1, 頂点2)」で追加できます。
1 2 3 4 5 | add_edge!(G1 , 1, 2) add_edge!(G1 , 1, 3) add_edge!(G1 , 2, 3) add_edge!(G1 , 2, 4) add_edge!(G1 , 3, 4) |
辺を足した結果を、プロット=表示してみましょう。
1 | gplot(G1, nodelabel= 1:4) |
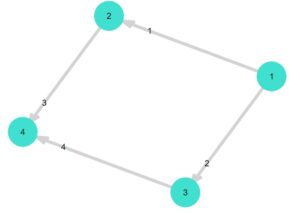
辺に向きのあるグラフ、有向グラフは、「DiGraph(頂点数)」で作れます。
1 2 3 4 5 6 | add_edge!(G2 , 1, 2) add_edge!(G2 , 1, 3) add_edge!(G2 , 2, 3) add_edge!(G2 , 2, 4) add_edge!(G2 , 3, 4) gplot(G2, nodelabel= 1:4) |
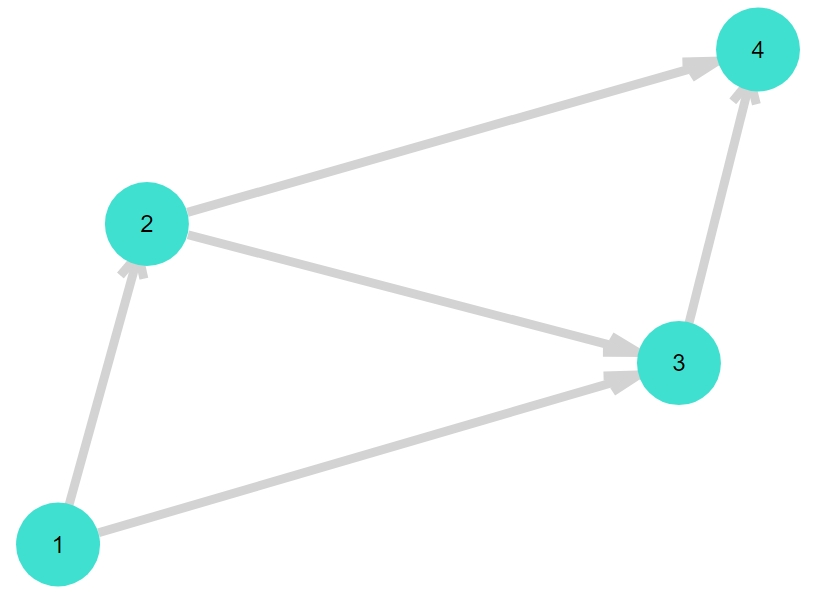
辺の追加「add_edge!(G2 , 1, 2)」は、始点\(1\)から終点\(2\)への辺の追加です。有向グラフなので、順序を変えると結果は変わります。
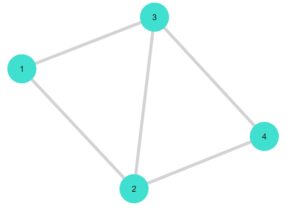
Graphs.jlでは、「smallgraph(型)」という関数で、あらかじめ用意された特定の形のグラフが作れます。
参考:Graphs.SimpleGraphs.smallgraph
1 2 | G3 = smallgraph(:diamond) gplot(G3, nodelabel= 1:4) |

ケーニヒスベルクの橋を表すグラフを、ここから作ってみましょう。
「add_vertices!(グラフ,頂点数)」で新たに頂点を追加できます。「rem_edge!(グラフ , 頂点, 頂点)」で辺を削除できます。
1 2 3 4 5 6 7 8 9 10 11 12 | G4 = smallgraph(:diamond) add_vertices!(G4,4) add_edge!(G4 , 1, 5) add_edge!(G4 , 1, 6) add_edge!(G4 , 2, 5) add_edge!(G4 , 2, 6) add_edge!(G4 , 2, 7) add_edge!(G4 , 2, 8) add_edge!(G4 , 4, 7) add_edge!(G4 , 4, 8) rem_edge!(G4 , 1, 2) rem_edge!(G4 , 2, 4) |
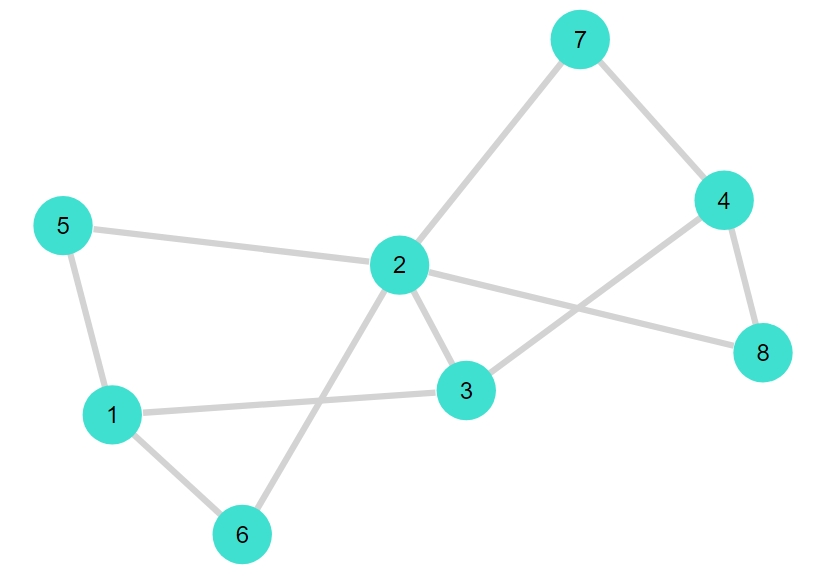
頂点と辺の個数、連結性、次数
グラフの頂点の個数は「nv(グラフ)」、辺の個数は「ne(グラフ)」で求められます。
1 2 | nv(G3) ne(G3) |
1 2 | 4 5 |
これを使うと、グラフのプロットのときの番号付けで、範囲をグラフに依存せずに指定できて便利です。
1 | gplot(G3, nodelabel= 1:nv(G3), edgelabel= 1:ne(G3)) |
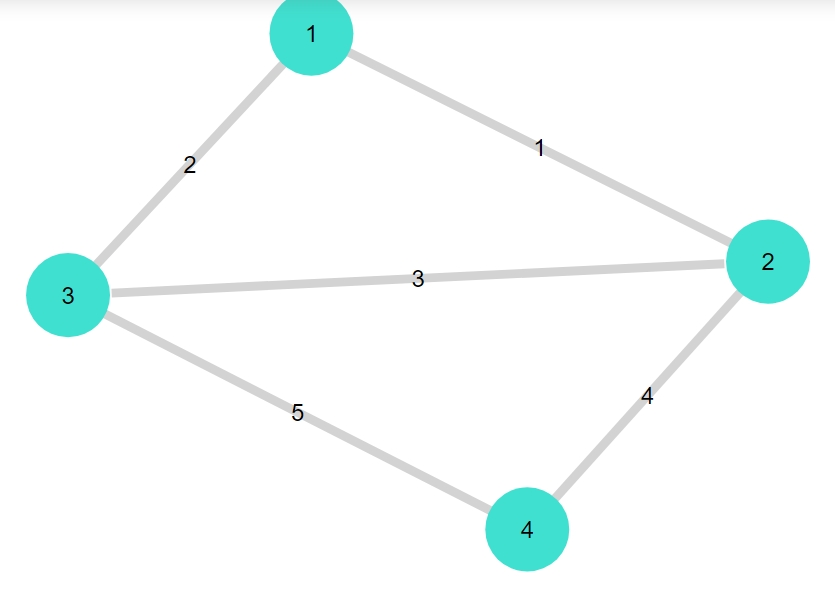
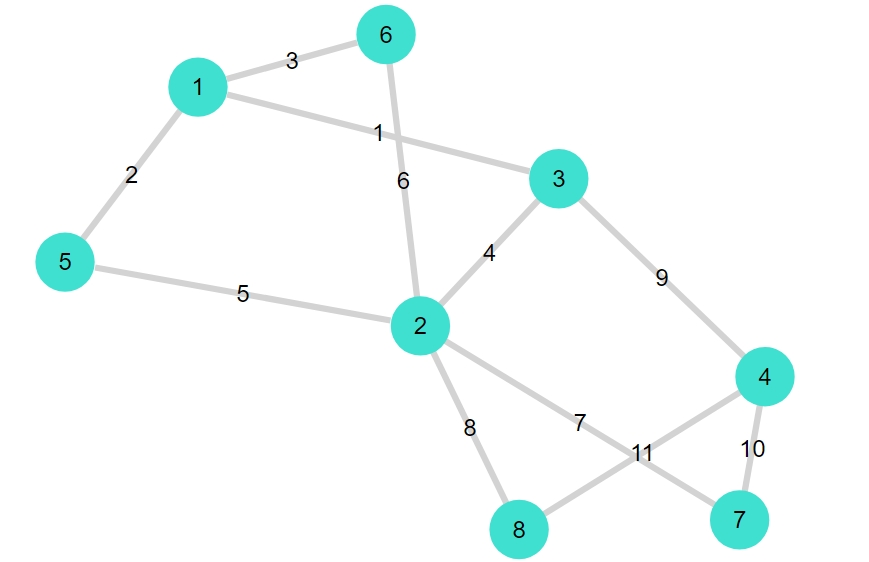
1 2 | nv(G4),ne(G4) gplot(G4, nodelabel= 1:nv(G4), edgelabel= 1:ne(G4)) |
1 | (8, 11) |
グラフが連結かどうかは、「is_connected(グラフ)」で判定できます。
1 2 | is_connected(G3) is_connected(G4) |
1 2 | true true |
「degree(グラフ)」で、グラフのすべての頂点の次数(次数列、スコア)が求められます。
1 2 | degree(G3) degree(G4) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 4-element Vector{Int64}: 2 3 3 2 8-element Vector{Int64}: 3 5 3 3 2 2 2 2 |
\(G_3, G_4\)どちらのグラフも連結で、奇数次数の頂点を持つので、一筆書きですべての辺を通って出発点に戻ってこれるような経路(オイラー経路)は存在しません。ただし、\(G_3\)については、奇数次数の頂点が2個なので、始点と終点が異なる一筆書きの経路(半オイラー経路)が存在します。
隣接行列
最後に、グラフの頂点と辺の情報をまとめた隣接行列の求め方を紹介しましょう。
行列\(A = (a_{ij})\)がグラフ\(G\)の隣接行列(adjacency matrix)であるとは、
\[a_{ij}= \begin{cases}1 & (Gが辺(i,j)を持つ)\\0 & (Gが辺(i,j)を持たない)\end{cases}\]
を満たすことです。
無向グラフのときは、辺\((i,j)\)があるときは辺\((j,i)\)もあると考えるため、隣接行列は対称行列になります。有向グラフのときは、辺\((i,j)\)と辺\((j,i)\)を区別し、一般に対称行列になるとは限りません。
Graphsでは「adjacency_matrix(グラフ)」で隣接行列を求められます。
1 2 | adjacency_matrix(G1) adjacency_matrix(G2) |
1 2 3 4 5 6 7 8 9 10 11 | 4×4 SparseArrays.SparseMatrixCSC{Int64, Int64} with 10 stored entries: ⋅ 1 1 ⋅ 1 ⋅ 1 1 1 1 ⋅ 1 ⋅ 1 1 ⋅ 4×4 SparseArrays.SparseMatrixCSC{Int64, Int64} with 5 stored entries: ⋅ 1 1 ⋅ ⋅ ⋅ 1 1 ⋅ ⋅ ⋅ 1 ⋅ ⋅ ⋅ ⋅ |
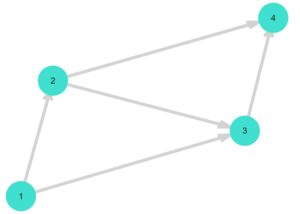
逆に、「Graph(行列)」か「DiGraph(行列)」で、隣接行列からグラフを作ることができます。
\(G_2\)の隣接行列の\((2,3)\)成分を0にすることで、辺\((2,3)\)を削除したグラフを作ってみましょう。
1 2 3 4 5 | A =adjacency_matrix(G2) A[2,3]=0 A G5 = DiGraph(A) gplot(G5, nodelabel= 1:nv(G5), edgelabel= 1:ne(G5)) |
1 2 3 4 5 6 7 | 4×4 SparseArrays.SparseMatrixCSC{Int64, Int64} with 5 stored entries: ⋅ 1 1 ⋅ ⋅ ⋅ 0 1 ⋅ ⋅ ⋅ 1 ⋅ ⋅ ⋅ ⋅ {4, 4} directed simple Int64 graph |
以上、Julia(Graphs)でグラフ理論におけるグラフ作成、次数、隣接行列を求める方法を紹介してきました。
頂点数や辺の数が増えるほど、可視化や手計算が難しくなるので、コンピュータで書けると便利ですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)