どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)でパラメータ付けられた曲線(平面、空間)を描く方法を紹介します。
準備
SymPy、Plots、PlotlyJSを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("SymPy") Pkg.add("Plots") Pkg.add("PlotlyJS") |
準備として、以下のコードを実行しておきます。
1 2 3 | using SymPy using Plots plotlyjs() |
パラメータ付けられた曲線(平面、空間)を描く方法
最初に、今回使う変数記号を用意しておきます。
1 | @vars t |
平面曲線\(c(t)=(x(t),y(t))\)は、「plot(x(t), y(t), tの範囲)」で描けます。
最も簡単な例として、円のパラメータ表示\(x(t)=\cos t , y=\sin t\)を描きましょう。
1 | plot(cos(t), sin(t), 0, 2*pi, aspect_ratio=:equal) |
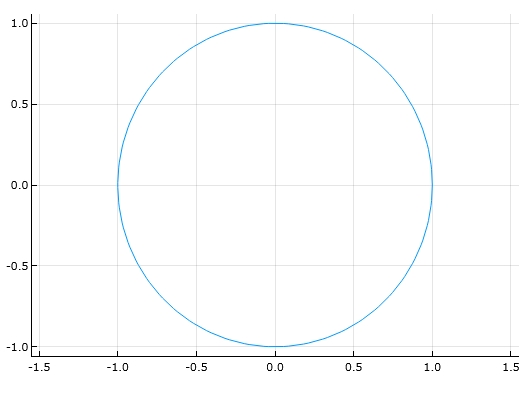
「aspect_ratio=:equal」によって、グラフのアスペクト比(縦横比)が等しくなります。
楕円
\[ \begin{aligned}(\frac{x}{a})^2+(\frac{y}{b})^2 =1\end{aligned} \]
のパラメータ表示は
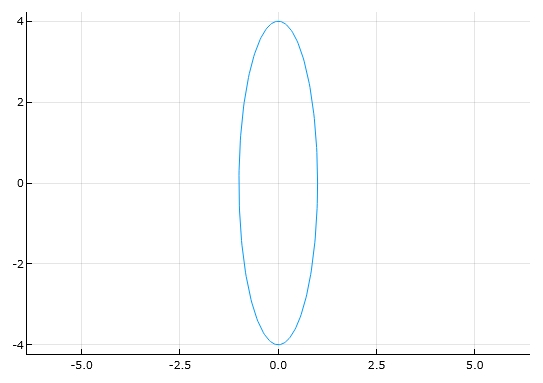
\[ \begin{aligned}x(t) =a\cos t , y(t)= b \sin t\end{aligned} \]
です。
1 | plot(cos(t), 4*sin(t), 0, 2*pi, aspect_ratio=:equal) |
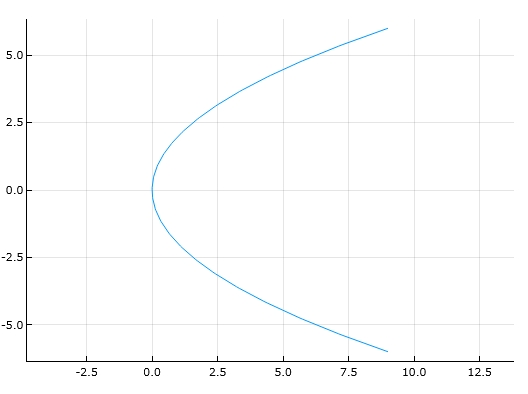
放物線
\[ \begin{aligned}y^2=4px\end{aligned} \]
のパラメータ表示は
\[ \begin{aligned}x(t)= pt^2,\quad y(t)= 2pt\end{aligned} \]
です。
1 | plot(t^2, 2*t, -3, 3, aspect_ratio=:equal) |
双曲線のパラメータ表示は\((\cosh t, \sinh t)\)と\((-\cosh t, \sinh t)\)です。2つ描いてみましょう。
1 2 | plot(cosh(t), sinh(t), -2, 2, aspect_ratio=:equal) plot!(-cosh(t), sinh(t), -2, 2, aspect_ratio=:equal) |

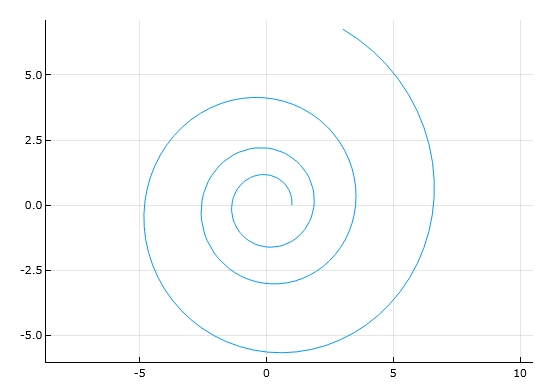
対数螺旋は、\((e^{at} \cos t, e^{at} \sin t)\)です。
1 | plot(exp(t/10)*cos(t), exp(t/10)*sin(t), 0, 20, aspect_ratio=:equal) |
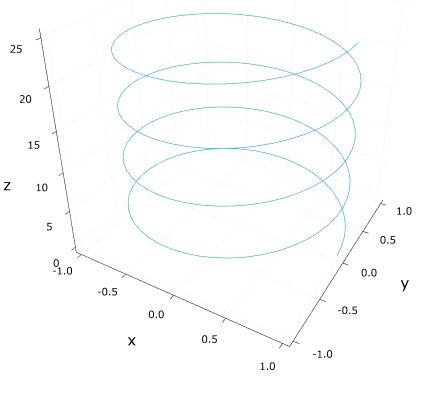
空間曲線も、同様の方法で描けます。つるまき曲線\((\cos t, \sin t, t)\)を描いてみましょう。
1 2 3 | plot(cos(t), sin(t), t, 0, 8*pi, size=(800,600), xlabel = "x", ylabel = "y", zlabel = "z") |
以上、Julia(SymPy)でパラメータ付けられた曲線(平面、空間)を描く方法を紹介してきました。
常微分方程式の解曲線を描くためにも使える方法です。簡単で使いやすいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
Julia(SymPy)で指数行列、線形常微分方程式を解く方法