どうも、木村(@kimu3_slime)です。
今回は、単位円盤を単位円盤に写す線形分数変換とは何か、その例を紹介します。
線形分数変換(一次分数変換)は、一般に\(f(z)=\frac{az+b}{cz+d}\)という形です。特に、
\[ \begin{aligned}f(z)= \frac{z-z_0}{\overline{z_0}z -1}\end{aligned} \]
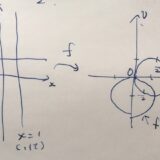
と表される線形分数変換は、単位円盤\(|z|\leq 1\)を単位円盤\(|w|\leq 1\)に写します。原点\(z=0\)が\(w=z_0\)という点に、\(z=z_0\)が中心\(w=0\)に写るものです。ただし、\(|z_0|<1\)を満たすものとします。
例として、\(z_0 =\frac{1}{2}\)としましょう。すると、
\[ \begin{aligned}f(z)= \frac{2z-1}{ z-2}\end{aligned} \]
となります。
単位円周\(|z|=1\)は、単位円周へと写っているでしょうか。
計算してみると、\(|z|=|\overline{z}|\)、\(|z|^2= z \overline{z}\)などに注意して、
\[ \begin{aligned}|f(z)| \\ = |\frac{2z-1}{ z-2}|\\ = \frac{|z| |\overline{2z-1}|}{|z-2|}\\ = \frac{|z| |2\overline{z}-1|}{|z-2|}\\ = \frac{ |2 z\overline{z}-z|}{|z-2|} \\ = \frac{ |2 |z|^2-z|}{|z-2|} \\ = \frac{ |2 -z|}{|z-2|}\\ =1\end{aligned} \]
となり、単位円周が単位円周に写っていることがわかります。
単位円盤の内部はどうでしょうか。単位円盤の内部では、分母が0にならないので、\(f\)は正則です。かつ、定数関数ではありません。したがって、複素解析における最大値の原理から、\(|f|\)は\(|z|<1\)において最大値を取らず、その境界\(|z|=1\)で取ります。したがって、単位円盤において\(|f(z)|<1\)であることがわかり、単位円盤が単位円盤へと写っていることがわかりました。
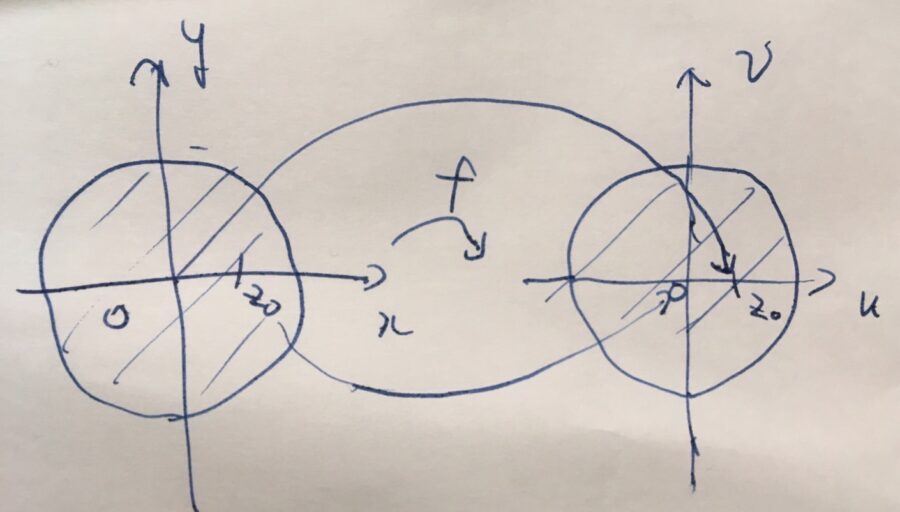
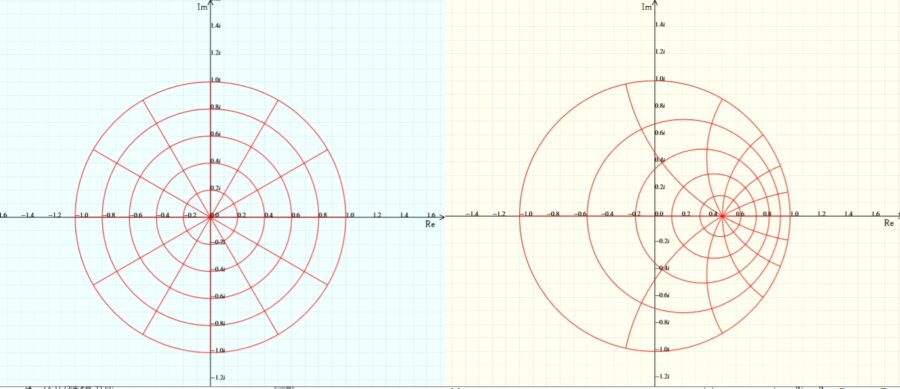
画像引用:複素関数で遊ぼう Webアプリ
この変換によって、単位円盤の形を保ったまま、中心をずらすことができます。例えば、非同軸のシリンダーにおけるポテンシャルを求める問題に応用できます(別記事で紹介予定)。
今回は、\(z_0=\frac{1}{2}\)のケースで確かめましたが、一般に\(|z_0|<1\)のとき、
\[ \begin{aligned}f(z)= \frac{z-z_0}{\overline{z_0}z -1}\end{aligned} \]
は単位円盤を単位円盤へと写す線形分数変換となっています。
一般に、開集合\(U\)をそれ自身に写すような全単射な正則関数(等角写像)を、\(U\)の自己同型写像(automorphism)と呼びます。\(f\)は単位円盤における自己同型写像の例です。
逆に、単位円盤における自己同型は、回転とこの形を組み合わせて、
\[ \begin{aligned}f(z)= e^{i\theta}\frac{z-z_0}{\overline{z_0}z -1}\end{aligned} \]
と表されることも知られています。証明にはシュワルツの補題を用います。エリアス・ラミ「複素解析」などを参照してください。
以上、単位円盤を単位円盤に写す線形分数変換とは何か、その例を紹介してきました。
円盤の形を保ったまま中心を動かし、問題を変形させるのに便利なものです。自己同型がこの形に限られるという結果も、面白いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Kreyszig, E: Advanced Engineering Mathematics
Wiley John + Sons (2011-05-03T00:00:01Z)
¥10,314 (中古品)
岩波書店 (2003-12-12T00:00:01Z)
¥2,640
日本評論社 (2009-06-01T00:00:01Z)
¥5,170
東京大学出版会 (1985-04-25T00:00:01Z)
¥3,740