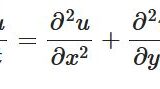どうも、木村(@kimu3_slime)です。
今回は、運動方程式から、1次元の波動方程式(弦の振動)\(\frac{\partial u}{\partial t}= c^2 \frac{\partial^2 u}{\partial x^2}\)を導出したいと思います。
考える状況は、次のようなものです。
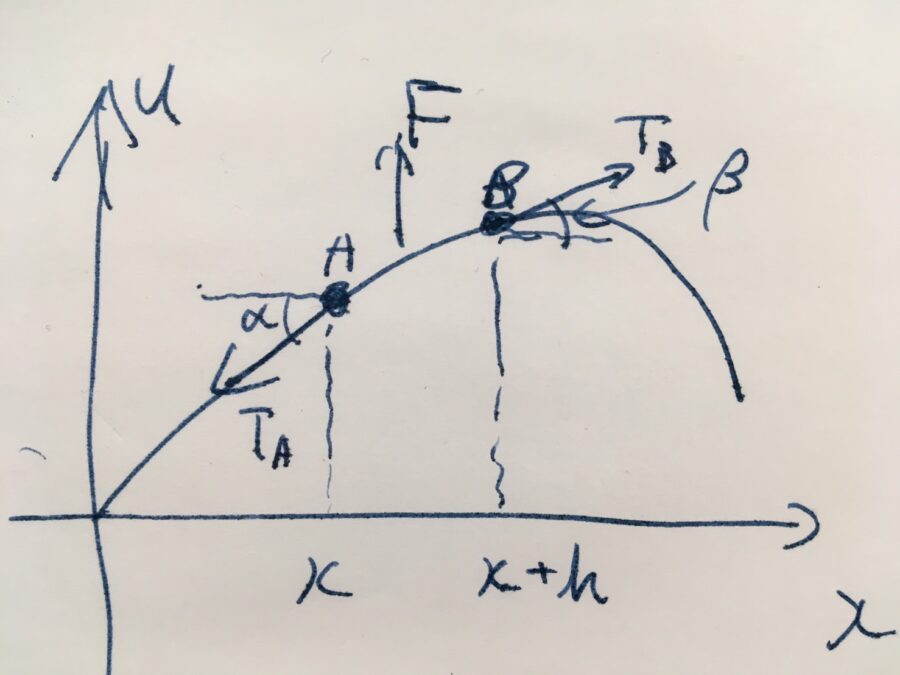
位置\(x\)、時間\(t\)における弦の変位を\(u(x,t)\)と関数で表すことにします。\(x\)から\(x+h\)という微小区間における力を考え、弦の運動方程式を立ててみましょう。
弦(string)とは、次のようなものと仮定します。
- 小さな粒子の集合体とする。弦の単位長さにおける重さは一定である(一様な弦)。微小区間における重さは\(m= \rho h\)と表せる。
- 張力は十分に強く、弦に対する重力は無視できるものとする。
- 微小部分は垂直方向に動く。弦が水平方向となす角の大きさは小さいものとする。
\(T_A,T_B\)を端点\(A,B\)における張力とし、水平方向となす角を\(\alpha,\beta\)とします。
仮定3より、水平方向に弦は動かないので、水平方向の張力は釣り合っています。そこで、\(T: = T_A \cos \alpha = T_B \cos \beta \)と置きましょう。
垂直方向に働く力は、仮定2より張力のみで、\(F= T_B \sin \beta – T_A \sin \alpha\)です。また、仮定1より微小部分の重さは\(m= \rho h\)です。
これらを使って、垂直方向の運動方程式を立てると、
\[ \begin{aligned}\rho h \frac{\partial^2 u}{\partial t^2}= T_B \sin \beta – T_A \sin \alpha\end{aligned} \]
となります。両辺を\(Th\)で割れば、サイン割るコサインでタンジェントが登場し、
\[ \begin{aligned}\frac{\rho}{T} \frac{\partial^2 u}{\partial t^2} = \frac{1}{h}(\tan \beta – \tan \alpha)\end{aligned} \]
です。ここでタンジェントは弦のなす傾きに等しいので、
\[ \begin{aligned}\tan \beta = \frac{\partial u}{\partial x}(x+h),\tan \alpha = \frac{\partial u}{\partial x}(x)\end{aligned} \]
となります。これを戻すと、
\[ \begin{aligned}\frac{\rho}{T} \frac{\partial^2 u}{\partial t^2} = \frac{1}{h}( \frac{\partial u}{\partial x}(x+h) – \frac{\partial u}{\partial x}(x))\end{aligned} \]
となり、ここで\(h \to 0\)という極限を取れば、右辺は微分の商の形(ニュートン商)なので、
\[ \begin{aligned}\frac{\rho}{T} \frac{\partial^2 u}{\partial t^2} =\frac{\partial^2 u}{\partial x^2}\end{aligned} \]
と波動方程式が得られました。\(c^2 =\frac{T}{\rho} \)と置くことで、
\[ \begin{aligned} \frac{\partial^2 u}{\partial t^2} =c^2\frac{\partial^2 u}{\partial x^2}\end{aligned} \]
という形で理論的には扱うことが多いです。\(c\)は波の移動速度に対応します。
以上、1次元の波動方程式(弦の振動)を、運動方程式から導出しました。
2次元(膜の振動)以上でも同様の考え方で、\(\frac{\partial u}{\partial t}= c^2 \Delta u\)という形が導けます。
右辺の空間2回微分は、水平方向の張力の釣り合いの結果ということがわかったと思います。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)