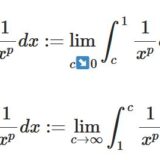広義積分の絶対収束の比較判定法：ガンマ関数を例に

どうも、木村（@kimu3_slime）です。

今回は、広義積分の絶対収束の比較判定法を紹介し、ガンマ関数を例に適用してみたいと思います。

絶対収束、比較判定法
ガンマ関数の絶対収束
こちらもおすすめ

絶対収束、比較判定法

今回紹介するのは、広義積分が絶対収束するための十分条件です。関数\(f\)の広義積分が絶対収束（absolute convergence）するとは、その絶対値\(|f|\)の広義積分

\[ \begin{aligned}\int_a^b |f(x)|dx =\lim_{c \searrow a} \int_c^ b |f(x)|dx\end{aligned} \]

が収束することです。左側の極限を考えていますが、右側の極限であっても同様に定義します。

広義積分は絶対収束するならば、収束します。（逆は正しくありません。）

考えている関数\(f\)が非負（正）値ならば、広義積分が収束することと絶対収束することは同値ですね。

既知の関数の積分であっても、原始関数を簡単な形（初等関数）で表すのは一般に難しいです。そこで、具体的な値がわからなくても、まずは広義積分が絶対収束しているか判定できたら嬉しいですね。その十分条件として、次のものが知られています。

広義積分の比較判定法（comparison test for improper integral）

区間\(I= (a,b]\)における関数\(f\)について考える。もし、

すべての\(x \in I\)に対し\(|f(x)|\leq g(x)\)
広義積分\(\lim_{c \searrow a} \int_c^ b g(x) dx\)は収束する

を満たす関数\(g\)が存在するならば、\(f\)の広義積分は絶対収束する。

一方で、

すべての\(x \in I\)に対し\(|f(x)|\geq h(x)\)
\(\lim_{c \searrow a} \int_c^ b h(x) dx= \infty\)

を満たす関数\(h\)が存在するならば、\(f\)の広義積分は絶対収束しない（発散する）。

左側端点の極限ではなく、右側端点の極限についても同様。

\( \int_c^b |f(x)| dx \leq \int_c^b g(x)dx \)と比較して、右辺が収束しているので、左辺も収束していると言えそうです。コーシーの収束判定条件と呼ばれる言い換えを使うと、実際に収束していると言えます。証明について詳しくは杉浦「解析入門 Ⅰ」を参照。

この条件を満たす\(g\)を優関数（majorant function）と呼びます。広義積分の絶対収束を示すには、広義積分が収束するような関数で上から評価できれば良いのです。

例えば、\(\int_1^\infty \frac{\sin x}{x^2} dx\)が絶対収束することを確かめてみましょう。\(|\frac{\sin x}{x^2}| \leq \frac{1}{x^2}\)で、\(\int ^\infty _1 \frac{1}{x^2}dx =[- \frac{1}{x}]_1^ \infty=1 \)と広義積分が収束するので、\(g(x)=\frac{1}{x^2}\)が優関数として使えます。比較判定法によって、元の積分は絶対収束すると言えました。

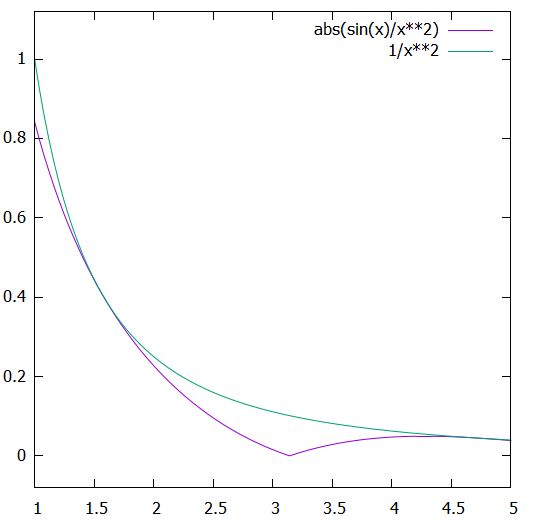
絶対値の積分\(\int |f |\)は、マイナスの部分を折り返したグラフの、正の部分の面積です。優関数は常にその上側に来るグラフで、その面積が有限値として収束するならば、当然\(\int |f|\)も収束しそうですね。これが比較判定法です。

この例のように、負のべき乗は比較関数として扱いやすいです。負のべき乗の広義積分の結果と比較判定法を組み合わせましょう。

オーダー（次数）による判定法

指数は\(p>0\)を満たすとする。

区間が\(I=(0,1)\)のケース
- \(|f(x)| \leq \frac{1}{x^p}\)、\(p<1\)ならば、\(f\)の広義積分は絶対収束
- \(|f(x)| \geq \frac{1}{x^p}\)、\(p \geq 1\)ならば、発散。
区間が\(I=(1,\infty)\)のケース
- \(|f(x)| \geq \frac{1}{x^p}\)、\(p<1\)ならば、発散。
- \(|f(x)| \leq \frac{1}{x^p}\)、\(p \geq 1\)ならば、絶対収束。

簡略化のために\((0,1),(1,\infty)\)の区間で考えたが、一般のケース\((a,b)\)でも類似の主張が成り立つ。

区間によって次数と収束・発散の関係が逆転することに注意。

\(\int_1^\infty \frac{\sin x}{x^2} dx\)のような形ならば、オーダーによる判定法ですぐに判定できますね。初等関数を使った積分は、テイラー展開でオーダーを見ることができれば、収束判定ができます。

もちろん、これによって判定できない場合もあり（ディリクレ積分 \(\int_0 \infty \frac{\sin x}{x}dx\)）、その場合はコーシーの収束判定条件を使う必要があるでしょう。

ガンマ関数の絶対収束

ガンマ関数は、

\[ \begin{aligned}\Gamma(x)=\int_0^\infty t^{x-1}e^{-t}dt\end{aligned} \]

という広義積分によって定義される関数です。これは階乗関数\(n!\)の一般化となっており、広義積分の例として重要なものです。

特殊なケースを除いて、その原始関数は初等関数で表せないことが知られているので、積分を直接計算することはできません。

そこで、\(x>0\)のとき、この広義積分\(\int_0^\infty t^{x-1}e^{-t}dt\)が収束していることを確かめてみましょう。

区間を\((0,a),(a,\infty)\)とうまく分けて、それぞれが絶対収束することを示します。被積分関数は正値であることに注意。

まず、無限遠方について。べき乗\(t^{x-1}\)よりの指数\(e^{-t}\)減衰の方が支配的なので、それが優関数として使えそうです。べきと指数の増大スピードの比較から、\(\lim _{t \to \infty} \frac{t^{x-1}}{e^{2t}}=0\)です（\(x\)は\(t\)に依存しない定数であることに注意）。したがって、\(t>a\)ならば\(\frac{t^{x-1}}{e^{2t}} \leq 1\)を満たす\(a\)が存在します。整理すれば、\(t^{x-1}e^{-t} \leq e^{-t}\)です。また、\(\int_a ^ \infty e^{-t} = [-e^{-t}]_a ^\infty = e^{-a}\)と広義積分は収束します。よって、比較判定法より、\(\int_a ^\infty t^{x-1}e^{-t}dt\)が収束することが言えました。

続いて、\((0,a)\)において。指数\(e^{-t}\)の影響は小さく、べき乗\(t^{x-1}\)の影響が大きそうなので、それを優関数として使いたいです。\( t^{x-1} e^{-x} \leq t^{x-1} e^{0}=\frac{1}{t^{1-x}} \)と評価できます。\(0<x<a\)より、\(1-a<1-x <1\)なので、オーダーによる判定法によって、\(\int_0^a t^{x-1}e^{-t}dt\)の収束が言えました。（\(1-x<0\)となるときは、\(\frac{1}{t^{1-x}}\)は負のべきではなくなってしまいますが、考えている区間が有界なので収束します。）

ガンマ関数の被積分関数のべき\(t^{x-1}\)は、ちょうど\(x>0\)のとき、オーダーによる判定法が使えるようになっていることに気づきますね。原点付近ではべき関数によって、無限遠方では指数関数によって、うまく収束するようになっています。

以上、広義積分の絶対収束の比較判定法を、ガンマ関数を例に紹介してきました。

直接計算できないような積分の収束を確かめるには、既知の関数と比較すれば良いわけです。その比較関数：優関数としては、負のべき乗や指数関数が使いやすいでしょう。広義積分を見たときに、関数の挙動を想定し、それが収束・発散しているか、一目で見抜けるようになったら嬉しいですね。

木村すらいむ（@kimu3_slime）でした。ではでは。