どうも、木村(@kimu3_slime)です。
今回は、グラフ理論における全域木とは何か、その求め方を紹介します。
全域木とは
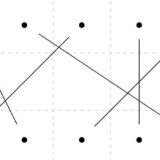
ある地域に、次のグラフで示すようなネットワークを組みたいとしましょう。辺を通じて、情報や電気などが伝わるとします。
通信網の建設には、ある程度のコストがかかるとします。そこで、全頂点がつながったまま、全体がつながるような辺の残し方はできないでしょうか。つまり、頂点を保ったままサイクルを持たない連結なグラフ(木)を求める問題、これが全域木の問題です。
\(G=(V,E)\)を抽象グラフとします。\(E^{\prime }\subset E\)として、\(G^{\prime}=(V,E^{\prime})\)が木となるとき、\(G^{\prime}\)をグラフ\(G\)の全域木(spanning tree)と呼びます。スパニング木とも。spanは数学では生成するという意味を持つので、グラフを生成する木、生成木と呼びたいですね。
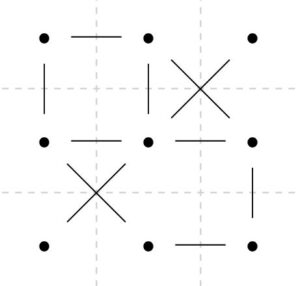
例えば、さきほどのグラフから点線で表した辺を除けば、サイクルを持たないグラフ、すなわち木になっています。これが元のグラフの全域木です。全域木は、元の頂点をすべて含んだ木であるような部分グラフです。
木は連結なので、元のグラフが連結でなければ当然全域木を見つけることはできません。
全域木の求め方
すべての連結なグラフには、全域木が存在します。全域木の構成方法はいくつか知られていますが、そのひとつを紹介しましょう。
全域木の求め方
\(G=(V,E)\)を連結なグラフで、頂点数を\(n\)、辺数を\(m\)とする。辺に適当に番号をつけて、\((e_1,e_2,\dots,e_m)\)と表す。
辺の集合の拡大列\(E_0,E_1,\dots,E_T\)を作る。構成の手順は次の通り。
- \(E_0 = \varnothing\)とする。
- \(i<m\)のときは次のように辺を増やす。
- \[ \begin{aligned}E_i= \begin{cases}E_{i-1}\cup \{e_i\} & ((V,E_{i-1}\cup \{e_i\})がサイクルを持たない )\\E_{i-1} & (それ以外)\end{cases}\end{aligned} \]
- \(i=m\)ならば停止する。そのときの辺の集合を\(E_T\)とする。
得られたグラフ\(G^{\prime}=(V,E_T)\)が全域木である。
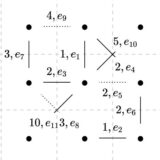
この方法で全域木が作れるか試してみましょう。まず、辺に適当に番号をつけます。
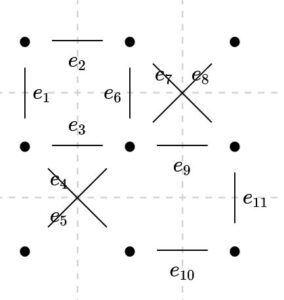
\(n=9,m=11\)です。\(E_0=\varnothing\)として、これにサイクルができない限り辺を加え続けましょう。
\(E_1,E_2,\dots, E_5\)までは辺が加わりますが、\(E_6\)のときは、\(e_6\)を加えるとサイクルができあがるので、\(E_6=E_5\)のままとなります。
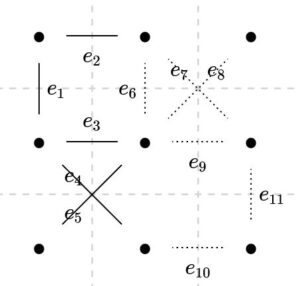
以降、\(E_7,E_8,E_{10}\)では辺が加わります。\(e_9,e_{11}\)を加えるとサイクルができるので、そこでは辺が加わりません。そしてすべての辺のチェックが終わった\(i=m=11\)なので、\(E_{11}\)が全域木です。
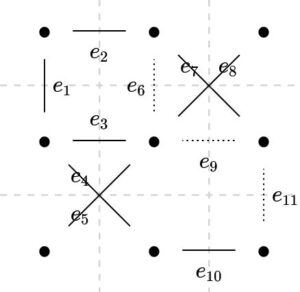
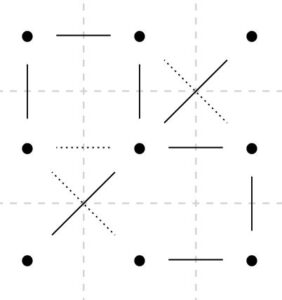
確かにこのグラフは全域木となっています。最初に提示した全域木とは異なりますが、あるグラフの全域木は一般に複数あるのが普通です。
証明については、「離散数学への招待〈上〉」を参照してください。
以上、グラフ理論における全域木とは何か、その求め方を紹介してきました。
辺に何らかのコストを考慮したグラフにおいて、そのコストを最小にする全域木を求める問題は、最小全域木を求める問題と呼ばれます。その導入として、まずは全域木とはどういうものかを知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガー・フェアラーク東京 (2002-12T)
¥1,773 (中古品)
丸善出版 (2012-07-17T00:00:01Z)
¥11,800 (中古品)
Graph Theory (Graduate Texts in Mathematics)
Springer (2018-06-05T00:00:01Z)
¥6,933