グラフ理論における2部グラフ、マッチング、結婚定理とは

どうも、木村（@kimu3_slime）です。

今回は、グラフ理論における2部グラフ、マッチング、結婚定理とは何かを紹介します。

2部グラフとは
マッチングとは
- コーニックの定理
- ホールの定理、結婚定理
こちらもおすすめ

2部グラフとは

例えば、電車やバスにおける座席を想像してみましょう。5つの空席があって、5人の人が座ろうか考えているとします。この状況は、グラフを使えば次のように表すことができるでしょう。

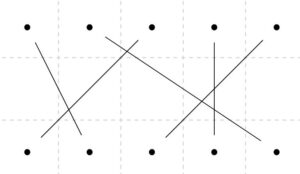
図の上側にある頂点が座席、下側の頂点が人を表すとします。そして、辺は座席と人の組み合わせ、すなわちマッチングを表すと考えられますね。おおざっぱにはこういう話です。

上のグラフにおいては、頂点が2つのグループに分かれています。より形式的に言えば、頂点の集合\(V\)が2つの集合\(V_1,V_2\)に分かれていて、\(V_1\)内、\(V_2\)内では異なる頂点が隣接しない（辺がない）グラフです。このようなグラフを、2部グラフ（bipartite graph）と呼びます。

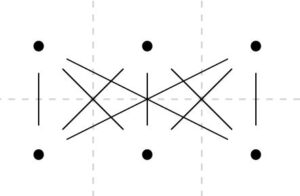
上のグラフ\(K_{3,3}\)は、異なるグループの間にすべて辺があるグラフで、完全な2部グラフと呼ばれています。

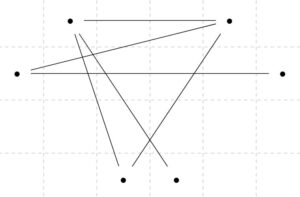
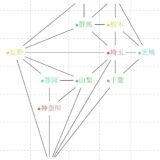
上のグラフは、2部グラフではありません。サイクルの部分が、どうやっても2つのグループに分けられませんね。一般に、2部グラフであることと、奇数個のサイクルを持つことは同値であると知られています。

しかし、左上、右上、下の3つのグループを考えれば、そのグループの中では辺を持っていません。すなわち、これは3部グラフです。一般に、\(k\)部グラフ（\(k\)-partite）を考えることができます。

彩色問題の言葉で言い換えれば、同じグループの中で辺がないので、同じグループを同じ色に、異なるグループを異なる色に塗り分けられます。すなわち、2部グラフは\(2\)-彩色可能であり、\(k\)部グラフは\(k\)-彩色可能です。

つまらないことですが、\(k\)個の頂点のグラフは、頂点をすべて別々のグループと考えてしまえば\(k\)-部グラフです。逆に言えば、\(2\)-部グラフは限られたケースのグラフと言えます。

マッチングとは

では、冒頭の座席と人のマッチングの話に戻りましょう。

例えば1席に2人以上が辺で対応するような状況は、マッチングとは言い難いです。グラフの辺の部分集合\(M\)がマッチング（matching）であるとは、\(M\)の辺がすべて独立している（independent）こと、すなわち辺が隣接していないことです。2つの辺が隣接しているとは、辺が共通する頂点を含んでいることですね。

グラフ\(G=(V,E)\)にマッチング\(M\)が与えられたとします。頂点の部分集合\(U\subset V\)について、\(U\)のすべての頂点が\(M\)の辺によって隣接しているとき、\(U\)の頂点は\(M\)によってマッチしている（matched）と言います。\(M\)のすべての辺によっても隣接しない頂点を、マッチしていない（unmatched）と呼びます。

席と人のマッチングのように、できるだけ多くの人がマッチする状態を探す問題が考えられます。与えられたグラフにおいて、その要素数が最大となるマッチングを最大マッチング（Maximum cardinality matching）と呼びましょう。

2部グラフのマッチングについては、次の結果が知られています。

コーニックの定理

コーニックの定理（König’s theorem）

\(G\)を2部グラフとする。\(G\)の最大マッチングの要素数は、\(G\)の頂点カバーの最小要素数に等しい。

ここで頂点の部分集合\(U \subset V\)がグラフ\(G\)の頂点被覆（vertex cover）であるとは、すべての辺\(E\)が\(U\)の頂点に隣接している（辺が要素として頂点を含んでいる）ことです。当然ですが、\(V\)自身は常に頂点被覆となります。

具体例で見てみましょう。

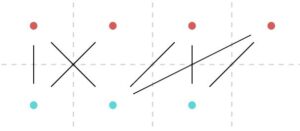
左2個の赤頂点は、一番左の青頂点とマッチするしかなくなります。右側の2個の赤、青の頂点はマッチさせられます。

したがって、緑で示した辺の集まりは最大マッチングで、その要素数は3です。

頂点被覆について考えます。次数の多い下側の頂点を候補として選んで、下の図に示しました。

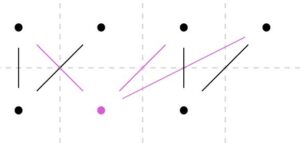
頂点で辺をカバーするには、どうやってもあと2つの頂点が必要となります。したがって、このグラフの頂点被覆の最小要素数は\(3\)です。コーニックの定理は確かに成り立っていますね。証明については「Graph Theory」を参照してください。

ホールの定理、結婚定理

ホールの定理（Hall’s theorem）、結婚定理（marriage theorem）

\(G=(V,E)\)を2部グラフとし、そのグループを\(A,B\)とする。

\(G\)が\(A\)のマッチングを持つことと、すべての\(U\subset A\)に対し、\(\mathrm{card}(U)\leq \mathrm{card}(N(U))\)が成り立つことは同値。

ここで、\(N(U)\)は\(U\)の近傍、\(U\)の頂点に隣接する頂点の集合。\(\mathrm{card}(U)\)は集合の要素数を表す。

再び具体例を通じて考えます。

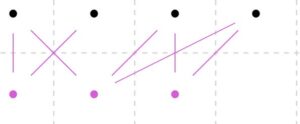
青の頂点の集合を\(A\)とすると、このグラフはマッチングを持ちます（緑の辺）。例えば\(U=A\)とすると、\(\mathrm{card}(U) =3\)で、隣接する点は赤頂点すべてなので\( \mathrm{card}(N(U))=4\)で、定理は確かに成り立っています。部分集合を考えても同様です。

そもそも、\(A\)のマッチングが存在する時、\(A\)の各頂点には隣接する\(B\)の頂点が最低1つはあります。したがって、すべての\(U\subset A\)に対し、\(\mathrm{card}(U)\leq \mathrm{card}(N(U))\)が成り立つのは確かなことです。その逆も成り立つ、というのが定理のポイントですね。

このグラフでは、赤の頂点\(B\)のマッチングを持ちません。\(U=B\)の要素数は\(4\)ですが、その隣接点\(N(B)\)の要素数は\(3\)となっています。定理は確かに成り立っていますね。

ホールの定理における対偶、\(A\)のマッチングを持たないならば、\(\mathrm{card}(U)> \mathrm{card}(N(U))\)を満たす\(U\subset A\)が存在することを、コーニックの定理から示しましょう。

グラフが\(A\)のマッチングを持たないとしましょう。\(G\)の最大マッチングの要素数は\(A\)の要素数より少ないので、コーニックの定理より\(A\)の要素数より少ない頂点被覆\(W\)が存在します。\(G\)は2部グラフなので、\(W = A^{\prime}\cup B^{\prime}\),\(A^{\prime}\subset A,B^{\prime} \subset B\),\(A^{\prime}\cap B^{\prime}= \varnothing\)と表せます。\(W\)は頂点被覆であり、その隣接する辺はすべての辺を含むので、\(A\backslash A^{\prime}\)の頂点は\(B^{\prime}\)の頂点としか結ばれません。つまり、\(\mathrm{card}(N(A\backslash A^{\prime}))\leq \mathrm{card}( B^{\prime})\)です。仮定より\(\mathrm{card}(A^{\prime})+\mathrm{card}(B^{\prime})=\mathrm{card}(W)<\mathrm{card}(A)\)なので、\(\mathrm{card}( B^{\prime})<\mathrm{card}(A)-\mathrm{card}(A^{\prime})=\mathrm{card}(A\backslash A^{\prime})\)です。よって、\(U=A\backslash A^{\prime}\)について主張が示せました。

以上、2部グラフとマッチング、結婚定理などを紹介してきました。

マッチングの問題は、席のマッチだけでなく、就職活動や合コン、広告や販売など人間社会のマッチングに応用できます。今回は異なるグループ間に辺があるかという条件だけでマッチングを考えましたが、辺の優先順位、すなわち個人がマッチしたい相手に優先順位をつけた問題を考えることもできます（安定結婚問題）。

マッチングの話題は、グラフの考え方が人間のネットワークの分析・効率化に役立ちそうと感じさせてくれますね。

木村すらいむ（@kimu3_slime）でした。ではでは。