どうも、木村(@kimu3_slime)です。
今回は、地図の塗り分け、グラフの彩色問題、四色定理について紹介します。
地図の塗り分け
グラフ理論において典型的な問題として、地図の塗り分け問題が知られています。「地図において隣り合った地域を必ず異なる色で塗るとき、何色の色で塗り分けることができるか?」という問題です。
例えば、次のような関東近郊の県、都を考えましょう。
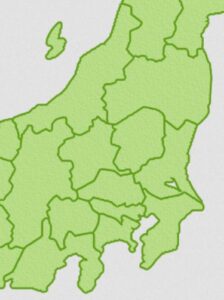
画像引用:日本地図のイラスト(県境入り) – Frameillust
この地図の色の塗り分け問題は、どのようにグラフで捉えたら良いでしょうか?
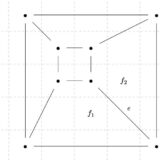
まず、地図は県境を辺とした平面グラフとして捉えられます。しかしそれは複雑な形をしていて捉えにくいです。そこで、地図における面(=各県)を頂点に、地図において隣り合った面(隣接する県)を辺に置き換えたグラフを考えましょう。(これを双対グラフ dual graph と言います。)
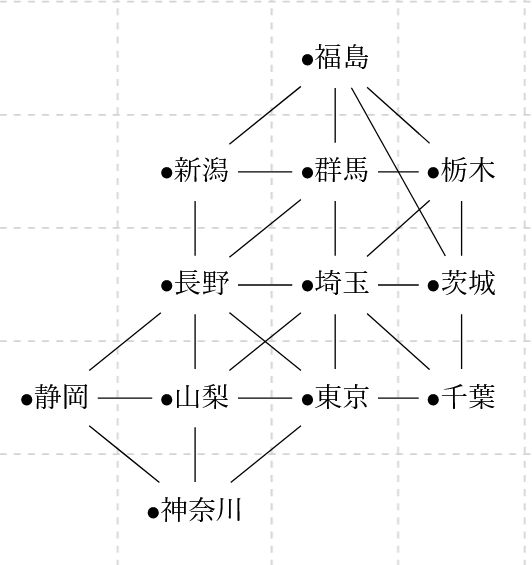
すると、上の図のようなグラフができあがります。辺が交差しているので平面グラフでないように見えますが、適切に表すことで辺の交差しない平面グラフになります。
もとの地図の面(県内)に色を塗るということは、双対グラフにおいて頂点を色を塗ることに対応していますね。そこで、隣接する頂点の色が異なるように、色を塗ってみましょう。
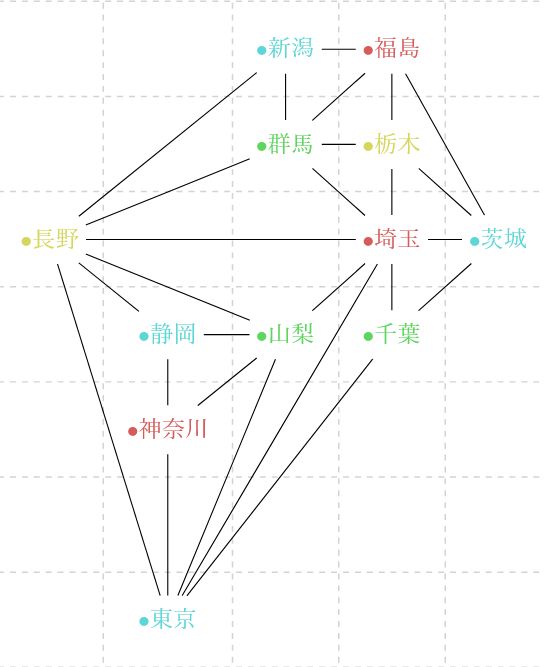
例えばこのグラフは、4色で塗り切ることができました。隣り合う県が異なる色で塗られているか、確かめてみてください。別の塗り方をいくつか試しますが、どうも3色では塗りきれない気がします。
グラフの彩色問題
グラフの頂点の塗り分け問題は、どのように定式化したら良いでしょうか。
各頂点に色を塗るということは、頂点に「赤、青、黄色、緑……」といった色を与えることです。色をたくさん、一般的に表すために、色を番号に置き換えてしまいましょう。1番目の色を\(1\)、2番の色を\(2\)と表すことにすれば、色が異なることを\(1\neq 2\)と数字で表すことができます。
すると、各頂点に色を塗ることは、頂点に対して色の数字を割り当てること、すなわち写像\(c:V\to \{1,2,\dots, k\}\)と表すことができます。例えば、\(c(埼玉)=1\)、\(c(茨城)=2\)といった具合です。
塗り分けの問題では、辺がある隣り合った頂点の間に塗られる色は必ず異なるようにします。\(G=(V,E)\)をグラフとしましょう。すべての頂点\(v,w\in V\)に対し、そこに辺がある\(\{v,w\} \in E\)ならば、\(c(v) \neq c(w)\)となるような写像\(c:V\to \{1,2,\dots, k\}\)を、グラフの彩色写像(coloring map of the graph)と呼びます。これは頂点の彩色ですが、辺や面の彩色を考えることもできます。
そして、終域 \(\{1,2,\dots, k\}\)の要素数が\(k\)である彩色写像が存在するとき、グラフは\(k\) – 彩色可能(\(k\) – colourable)と呼ばれます。また、あるグラフの最小の彩色可能な色数を、彩色数(chromatic number)と呼びます。
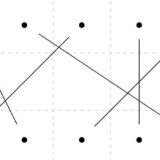
さきほど見た地図は、\(3\) – 彩色不可能であるように見えました。部分的に取り出したグラフをもとに、考えてみます。
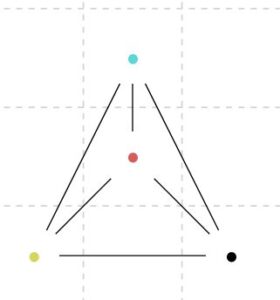
これは\(K_4\)と呼ばれる、\(4\)頂点の間にすべて辺があるグラフです。当然ですが、4頂点なので、\(4\) – 彩色可能です。(\(n\)頂点のグラフは\(n\)-彩色可能ですね。)
しかし、3色で塗り分けることはできません。例えば、赤、青、黄と頂点に色を塗っていきます。残りの色が塗られていない黒の頂点を、何色で塗れば良いでしょうか。赤、青、黄のどの色だとしても、他の3頂点と隣接しているので、ありえません。よって、\(3\)-彩色不可能です。つまり、このグラフの彩色数は\(4\)です。
一般に、\(n\)個の頂点を持ち異なる頂点間にすべて辺があるグラフ\(K_n\)(完全グラフ)の彩色数は、\(n\)になります。
四色定理とは
さて、地図は平面グラフとして表せますが、最小何色で塗り分けられるのでしょうか? 「平面グラフは\(k\)-彩色可能か?」という問題は、\(k\)色問題(\(k\)-color problem)と呼ばれています。
四色定理(four color theorem)
平面グラフは、\(4\)-彩色可能である。
最初にこの主張は1852年に予想されましたが、1890年には5色のケースで証明されます。4色定理はより難しく、コンピュータによって有限個の可能性のチェックを行った証明のみが現在では知られています。証明そのものをチェックする複数の論文があり、現在では正しいと考えられています。
参考:K. Appel, W. Haken, “Every planar map is four colorable” (Bulletin of the American Mathematical Society Volume 82, Number 5, September 1976)
参考:”A new proof of the four-colour theorem” by Neil Robertson, Damiel P. Sanders, Paul Seymour, and Robin Thomas (Electronic Research Announcements of the American Mathematical Society Volume 2, Number 1, August 1996)
参考:Gonthier, Georges (2008), “Formal Proof—The Four-Color Theorem” , Notices of the American Mathematical Society, 55 (11): 1382–1393, MR 2463991
今回は簡単なケースとして、六色定理をざっくりと示してみましょう。
グラフ\(G=(V,E)\)の頂点の数\(n\)に関する数学的帰納法で示します。
\(n\leq 6\)のとき、それぞれ異なる色を割り当てれば良いだけで、6-彩色可能です。
\(n=k,k \geq 6\)のとき6-彩色可能であると仮定して、\(n=k+1\)のとき6-彩色可能であることを示しましょう。
一般に、連結な平面グラフには次数\(5\)以下の頂点が少なくともひとつ存在することが知られています。(オイラーの公式、握手の補題などを使って証明できる)
その頂点を\(v\)とします。\(G\)から頂点\(v\)、隣接する辺を取り除いたグラフを\(G^{\prime}\)としましょう。帰納法の仮定より、\(G^{\prime}\)は6-彩色可能です。
\(G^{\prime}\)の彩色写像を用いて、\(G\)の頂点\(v\)に適切に色を割り当てられます。なぜなら、\(v\)の次数は\(5\)以下なので、隣接する頂点の色は最大\(5\)色で、それと異なる色を割り当てれば良いので。よって、\(G^{\prime}\)に\(v\)と隣接する辺を加えたグラフ\(G\)は、6-彩色可能であることが示せました。
以上、地図の塗り分け、グラフの彩色問題、四色定理とは何か、六色定理の証明を紹介してきました。
地図の塗り分け問題なら、子どもでも理解できる問題ですし、四色定理も主張自体は多くの人が理解することができるでしょう。にもかかわらず、コンピュータを用いない簡単な証明が知られていないのは、問題が奥深いと感じますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
シュプリンガー・フェアラーク東京 (2002-12T)
¥1,773 (中古品)
丸善出版 (2012-07-17T00:00:01Z)
¥11,800 (中古品)
Graph Theory (Graduate Texts in Mathematics)
Springer (2018-06-05T00:00:01Z)
¥6,933