グラフ理論におけるオイラーの公式とは、証明、多面体定理

どうも、木村（@kimu3_slime）です。

今回は、グラフ理論におけるオイラーの公式を紹介します。

オイラーの公式とは
オイラーの公式の証明
オイラーの多面体定理
こちらもおすすめ

オイラーの公式とは

オイラーの公式（Euler’s formula）は、平面グラフの頂点、辺、面の個数に関する恒等式です。

\(G\)を連結な平面グラフ、\(\mathrm{card}(V),\mathrm{card}(E),\mathrm{card}(F)\)をそれぞれ頂点、辺、面の個数とする。次の等式が成り立つ。

\[ \begin{aligned}\mathrm{card}(V)-\mathrm{card}(E)+\mathrm{card}(F)=2\end{aligned} \]

（複素解析におけるオイラーの公式\(e^{i\theta}= \cos \theta + i \sin \theta\)とは別物です。）

オイラーの公式が正しいかどうか、具体例で確かめてみましょう。

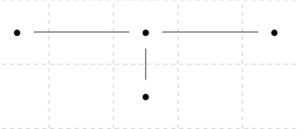
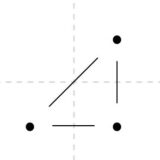
上のグラフでは、\(\mathrm{card}(V)=4\)、\(\mathrm{card}(E)=3\)、\(\mathrm{card}(F)=1\)なので、\(4-3+1=2\)は成り立っています。平面グラフの面とは、グラフによって囲まれる「内側」の部分だけでなく、外側もカウントすることに注意しましょう。

このグラフは、サイクルを持たず、木です。木では\(\mathrm{card}(V)=\mathrm{card}(E) +1\)が成り立つことを確かめました。面の数が\(1\)個なので、木に関してはオイラーの公式\(\mathrm{card}(V)-\mathrm{card}(E)+\mathrm{card}(F)=2\)は確かに成り立っています。

他のグラフを考えましょう。

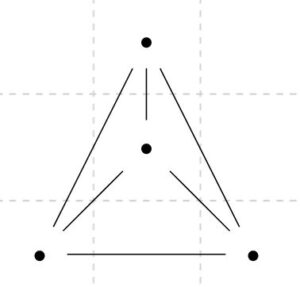
上のグラフでは、\(\mathrm{card}(V)=4\)、\(\mathrm{card}(E)=6\)、\(\mathrm{card}(F)=4\)なので、\(4-6+4=2\)で、オイラーの公式は成り立ちます。

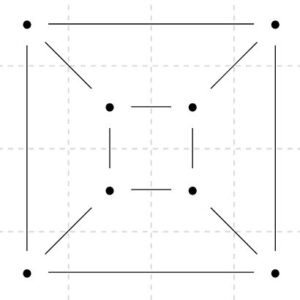
このグラフでも、\(\mathrm{card}(V)=8\)、\(\mathrm{card}(E)=12\)、\(\mathrm{card}(F)=6\)なので、\(8-12+6=2\)でオイラーの公式は成り立ちます。

グラフが木であるときには、オイラーの公式は成り立っています。今回知りたいのは、それが木でなくなるとき、サイクルを持つときどうなるか、ということです。

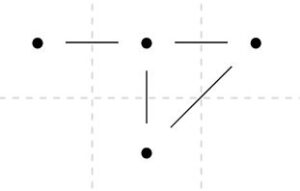
木にひとつ辺を加えて、サイクルができたとします。1個辺が増えて、それによって面が1個増えるので、\(\mathrm{card}(V)-\mathrm{card}(E)+\mathrm{card}(F)=2\)という関係式は保たれ続けますね。つまり、辺の数を1つずつ増やしていく帰納法によって、一般の場合も証明できそうです。

オイラーの公式の証明

では、オイラーの公式の証明をしましょう。

グラフ\(G\)の頂点の数\(\mathrm{card}(V)\)を任意とし、辺の数\(n=\mathrm{card}(E)\)に関する数学的帰納法で示します。また、サイクルを持つか持たないかで場合分けします。

\(n=0\)のときは、（空でない）連結なグラフを考えているので、\(\mathrm{card}(V)=1\)です。このとき面は1つです。したがって、\(\mathrm{card}(V)-\mathrm{card}(E)+\mathrm{card}(F)=2\)は成り立ちます。以降では、\(n=k-1\)のときの主張の成立を仮定し、\(n=k\)で成立するかどうかを確かめましょう。

\(G\)がサイクルを持たない、すなわち木のときは\(\mathrm{card}(V)=\mathrm{card}(E) +1\)が成り立つことを以前示しました。木では面の数が1個なので、\(\mathrm{card}(V)-\mathrm{card}(E)+\mathrm{card}(F)=2\)が成り立ちます。

\(G\)がサイクルを持つときを考えます。そのサイクルに含まれる辺のひとつを\(e\)とし、\(G\)から\(e\)を除いたグラフを\(G^{\prime}\)とします。

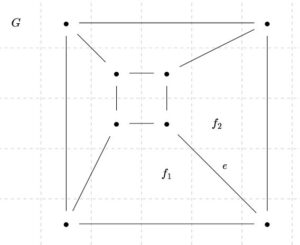
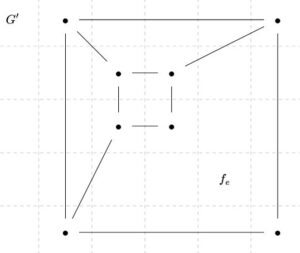
\(G\)は連結なので、サイクルから1つの辺を除いた\(G^{\prime}\)も連結です。帰納法の仮定より、\(\mathrm{card}(V(G^{\prime}))-\mathrm{card}(E(G^{\prime}))+\mathrm{card}(F(G^{\prime}))=2\)が成り立ちます。

ジョルダンの曲線定理より、\(e\)は\(G\)の2つの面\(f_1,f_2\)の境界を含んでいます。そして、\(e\)は\(G^{\prime}\)の辺ではないので、\(e\)の内部を含むような\(G^{\prime}\)の面\(f_e\)が存在します。このとき、\(f_1,f_2,f_e\)以外の面は、\(G,G^{\prime}\)の間で変化しません。

したがって、面の個数に注目すれば、\(G\)は\(G^{\prime}\)より1個多くなります。\(G^{\prime}\)の定義より、辺も1個多いのでした。よって、帰納法の仮定と合わせれば、\(\mathrm{card}(V(G))-\mathrm{card}(E(G))+\mathrm{card}(F(G)=2\)が成り立つことがわかりました。

オイラーの多面体定理

今回紹介したのは平面グラフですが、立体的な図形、凸多面体についても同様の結果が成り立つことが知られています。

\(\mathrm{card}(V),\mathrm{card}(E),\mathrm{card}(F)\)を凸多面体の頂点、辺、面の個数とする。次の等式が成り立つ。

\[ \begin{aligned}\mathrm{card}(V)-\mathrm{card}(E)+\mathrm{card}(F)=2\end{aligned} \]

例えば上の平面グラフは、正四面体、立方体（正六面体）を平面グラフに落とし込んだものです。普通に立方体を平面上に描くと、面の影になって辺が交差する部分が生まれてしまいますが、「裏側」の面を外側の1つの面としてグラフで表すことはできます。このように、多面体の性質を平面グラフに落とし込んで、オイラーの公式を適用することができます。

多面体の例として有名なのは、正四面体、正六面体、正八面体、正十二面体、正二十面体といった正多面体です。これらはプラトン立体とも呼ばれています。

正多面体とは、平面グラフとして見れば、頂点の次数\(d\)、面に隣接する辺の数\(k\)がすべて一定のものです。例えば立方体なら、\(d=3,k=4\)です。正多面体であると、\(d,k \geq 3\)となり、この条件とオイラーの公式、握手の補題から、\(d,k \)が限られた5通りしかないことが示せます。詳しくは「離散数学への招待〈上〉」を参照。

以上、オイラーの公式と具体例、証明、多面体定理について紹介してきました。

オイラーの公式に登場する、頂点、辺、面の個数に関する交代和のようなものは、位相幾何学（トポロジー）においてオイラー標数として一般化されます。図形の性質を量として捉える、というのはとても便利な議論です。

オイラーの公式は、一見すると不思議な等式に見えますが、簡単なケースから考えれば確かに成り立つ内容です。木のケースと違って、面が生まれるケースも考慮に入れた等式なのがポイントですね。

木村すらいむ（@kimu3_slime）でした。ではでは。