グラフ理論における次数、握手の補題とは

どうも、木村（@kimu3_slime）です。

今回は、グラフ理論における次数、握手の補題について紹介します。

次数とは
次数の性質、握手の補題
こちらもおすすめ

次数とは

グラフ\(G\)とは、有限個の点の集まり＝頂点\(V\)と、頂点2点からなる辺の集合\(E\)をあわせたものでした。

グラフの特徴を表すための量として有名なのが、次数です。頂点\(v \in V\)の次数（degree）とは、\(v\)を含む辺の個数のことで、それを\(\mathrm{deg}(v)\)と表します。

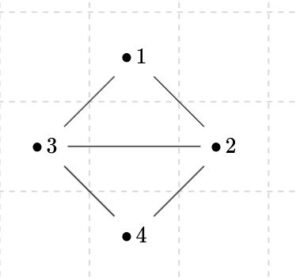
上図のグラフにおいては、\(\mathrm{deg}(1)=\mathrm{deg}(4)=2\)、\(\mathrm{deg}(2)=\mathrm{deg}(3)=3\)です。

次数は、化学における原子価、ある原子が他の何個の原子と結びつくかを表す「腕の数」と似ていますね。水分子\(\mathrm{H_2 O}\)では、構造式は\(\mathrm{H-O-H}\)で、\(\mathrm{H}\)の次数は\(1\)、\(\mathrm{O}\)の次数は\(2\)です。この記事では、辺の重複は許容しない単純グラフを考えているので、二重結合などのケースは考えていません。

次数は次のように言い換えることができます。

頂点\(v,w\in V\)が隣接している（adjacent）とは、\(\{v,w\} \in E\)とします。上で示したグラフならば、\(1,2\)は隣接していて、\(1,4\)は隣接していません。

頂点\(v\)の近傍（neighbor）を、\(N(v) :=\{w \mid w は vと隣接している\}\)と定めましょう。上で示したグラフならば、\(N(1)=\{2,3\}\)、\(N(2)=\{1,3,4\}\)です。

こうすれば、\(\mathrm{deg}(v) = \mathrm{card}( N(v))\)です。\(\mathrm{card}(A)\)は集合\(A\)の要素の個数（濃度）を表します。

ある頂点の次数は、その頂点を含む辺の個数、すなわち辺がある隣り合った頂点の個数、というわけです。

次数の性質、握手の補題

では、次数の性質について考えていきましょう。

同型なグラフ\(G_1,G_2\)を考えると、次数という量は同型写像によって保存されます。同型写像を\(F\)とすると、\(\mathrm{deg}_{G_1}(v) = \mathrm{deg}_{G_2}(F(v)) \)です。

\(d=\mathrm{deg}_{G_1}(v)\)と置くと、\(v\)と隣接する頂点は\(d\)個あるので、それを\(v_1,\dots,v_d\)としましょう。\(F(v)\)と隣接する点は\(F(v_1),\dots ,F(v_d)\)であることがわかります。詳しく言えば、\(F\)はグラフの同型写像なので、\(\{v,v_k\} \in E(G_1)\)は\(\{F(v),F(v_k) \} \in E(G_2)\)と同値です。よって、\(F(v)\)の隣接点は\(d\)個、\(d=\mathrm{deg}_{G_2}(F(v))\)がわかりました。

あるグラフ\(G\)のすべての頂点の次数を、広義単調減少となるように並べた列\((\mathrm{deg}(v_1),\mathrm{deg}(v_2),\dots, \mathrm{deg}(v_N)\)を、\(G\)の次数列（degree sequence）、またはスコア（score）と呼びます。さきほどから例として用いているグラフの次数列は、\((3,3,2,2)\)です。

グラフの頂点の個数、辺の個数、次数列は、グラフの同型写像によって変化しません。このような量を、グラフの不変量（invariant）と呼びます。

2つのグラフが同型ならば不変量は一致しますが、逆に不変量が等しいからといって同型であるとは必ずしも言えないことに注意しましょう。

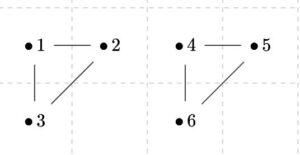
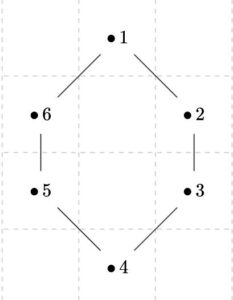
この2つのグラフは、頂点が\(6\)個、辺が\(6\)個で、次数列は\((2,2,2,2,2,2)\)と一致しています。しかし、グラフとして同型ではありません。

端的に言えば、上のグラフは2つの部分に分かれているのに対し、下のグラフは1つで分かれていないので。これに関しては、グラフの経路や連結の話を別記事でする予定です。

次数の基本的な性質として、握手の補題（handshake lemma）があります。次数和の公式とも。

\(G=(V,E)\)を任意のグラフとする。

\[ \begin{aligned}\sum_{v\in V}\mathrm{deg}(v) = 2 \mathrm{card}(E)\end{aligned} \]

ただし、\(\mathrm{card}(E)\)は辺の個数を表す。

さらに、奇数次数の頂点の個数は、偶数となる。

確かめましょう。任意の辺\(1\)つを考えると、それは必ず\(2\)つの頂点を含みます。次数すべてを足し合わせるということは、すべての辺が含む頂点の数を足し合わせるということなので、それは\(2 \mathrm{card}(E)\)となることがわかりました。

\(\sum_{v\in V}\mathrm{deg}(v) = 2 \mathrm{card}(E)\)において右辺は偶数なので、左辺も偶数でなければなりません。左辺は奇数次数と偶数次数の和ですが、奇数次数の部分の和が偶数でなければ、左辺は偶数となりません。よって、奇数次数の頂点の個数は、偶数となることがわかりました。

実際、上のグラフでは、奇数次数の頂点は\(2,3\)の\(2\)つ、偶数個となっています。奇数次数の頂点が1つあれば、最終的にペアとなる奇数次数の頂点がなければならないのです。余った「手」を結ぶ法則ということで、握手の補題と呼ばれています。

以上、グラフ理論における次数、握手の補題を紹介してきました。

次数は、「グラフが一筆書きできるか」という特徴を表すために使われます。グラフを量的に分析する方法のひとつとして、次数の考え方をマスターしましょう。

木村すらいむ（@kimu3_slime）でした。ではでは。