どうも、木村(@kimu3_slime)です。
\(6 \div 2 (1+2)\)の答えは、9でしょうか。1でしょうか。この簡単だが解釈の分かれる問題は、2011年からインターネット上で話題になっているようです。
今回は、この問題は式の解釈を決めないと答えが定まらないことを紹介し、したがって「出題者はカッコを用いるべき」という結論を導きます。
2通りの解釈が可能な数式
この数式は、2通りの解釈ができます。それによって、異なる答えが導かれます。
\[ \begin{aligned}6 \div 2 (1+2)=(6\div 2)(1+2)= 3 \times 3 =9\end{aligned} \]
\[ \begin{aligned}6 \div 2 (1+2)=6\div (2(1+2))=6 \div 6=1\end{aligned} \]
したがって、計算の解釈方法の明示がない限りは、これは問題として不適切です。
数式計算の優先順位として、アメリカでスタンダードなものが「PEMDAS」です。
P Parentheses first
E Exponents (ie Powers and Square Roots, etc.)
MD Multiplication and Division (left-to-right)
AS Addition and Subtraction (left-to-right)
引用:Order of Operations – PEMDAS
かっこ、指数(べきや平方根)、乗法と除法、加法と減法の順に優先される、というルールです。そして、乗法と除法、加法と減法においては、左から右に計算するというルールです。日本の学校教育でも、「左から右に計算する(と読む)」のが標準であるはずです。
これにのっとれば、
\[ \begin{aligned}6 \div 2 (1+2)=6\div 2\times 3= 3 \times 3 =9\end{aligned} \]
と解釈されます。したがって、この立場からすれば答えは9です。
Google検索や、WolframAlphaでは、\(6 \div 2 (1+2)\)は\((6\div 2)\times( 1+2)\)として解釈され、答えは\(9\)です。一方で、プログラミング言語Juliaでは、かけ算の記号\(*\)を省略するかしないかによって、結果が変わります。

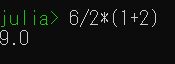
つまり、どのような計算式として解釈すべきかが定まっていない、曖昧だと、答えが的確に返ってこないのです。これはコンピュータに問題を与える人間側の問題です。
解釈の仕方、計算の優先順位の付け方には、ただひとつの答えはありません。どちらの流儀で解釈しても良いとは思います。どちらでも良いですが、解釈方法を曖昧さのないように述べるべきです。問題として出題する以上は、解釈によって答えが変わるような曖昧な問題は不適切と言えます。
出題者はカッコを使うべきである
\(6 \div 2 (1+2)\)という式に限らず、中学校レベルの「文字と式」において、解釈の分かれる式が出題されているようです。
実際に高校入試で類似の問題が出題されており、そのことについて教育委員会に問い合わせた方がいます。

確かに、このような記述を僕も中学校の頃に見ました。しかし、これは不適切な問題だと思っています。さきほどの問題と全く同じです。
\[ \begin{aligned}8xy \div 4x = 8\times x\times y\div 4 \times x\end{aligned} \]
\[ \begin{aligned}8xy \div 4x = 8xy \div (4x)=\frac{8xy}{4x}\end{aligned} \]
と解釈することができますが、両者の結果は変わってしまいます。
曖昧さなく後者の意図で出題するならば、\(8xy \div (4x)\)とかっこをつけて書くべきです。(または、最初から分数の形で出題するべきです。分数の形ならば分母と分子のまとまりは明確になります。高校以降の数学で、\(\div\)が使われずに分数が主流となるのは、解釈の曖昧さをなくす理由があるかと思います。)
「教科書にはそう書いてあるから、この回答は正しい」という結論は妥当ではありません。これは計算例、解釈例にすぎないものです。\(8xy \div 4x = 8xy \div (4x)\)と見るならば、ここでは「左から計算する」という法則が破られてしまい、生徒は混乱するでしょう。
「かけ算とわり算が混同した式において、かけ算の省略記号が使われていたら、そこを優先して計算する」というルールを明示すれば妥当な式ですが、暗黙にそう読めというのは数学の問題として適切ではありません。
この文字と式、代数における慣習的な記法の問題は、100年前から議論されていたようです。
参考:「6÷2(1+2)」問題は100年前にも議論されていた – 山月記
\(9a^2 \div 3a \)という式を、\(9a^2 \div (3a) =\frac{9a^2}{3a}\)の意味で解釈することが、慣習的に行われていたようです。しかしこの記法は、かっこをつけなければ、乗法や除法を左から計算するという方法と矛盾します(暗黙にカッコを補うことで、右から計算している)。
以上、\(6\div2(1+2)\) の答えは9か1かという問題について、解釈の余地が生まれる良くない問題であり、出題者はカッコを補うべき、という話をしました。
- かっこを使わなければ:式に多義的な解釈が生まれ、答えが2通り生まれる
- かっこを使えば:解釈の余地はなく、答えが1つに定まる
つまり、\(6\div\{2(1+2)\}\)か\((6\div2)(1+2)\)と書くのが問題として適切でしょう。こう書けば解釈の方法、答えは1通りになります。
数と式の理解度を問いたいならば、出題者はカッコを使い、余計な解釈の余地を残さないようにしたほうが良いと思います。簡単な問題ですが、きちんと定義や解釈の定まった見方を、数学教育者は示したいものですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
偶数+奇数はいつでも奇数? 読み解き方、よくある間違いと証明