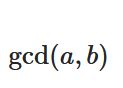素数の性質：無限にあること、素因数分解の一意性と応用

どうも、木村（@kimu3_slime）です。

素数は、整数の構成要素とも呼べる数で、整数論において重要な役割を果たしています。

今回は、整数の重要な性質、無限にあること、素因数分解の一意性と応用について紹介します。

素数が無限にあること
素因数分解の一意性と応用
こちらもおすすめ

素数が無限にあること

素数とはなんでしょうか。\(2,3,5,7\)は素数の例です。\(2\)の（正の）約数は\(1\)と\(2\)だけ、\(5\)の約数は\(1\)と\(5\)だけです。

\(2\)以上の整数\(x\)が素数（prime number）であるとは、\(x\)の正の約数が\(1\)と\(x\)のみであることです。

例えば、\(4\)は素数ではありません。\(4=2\times 2\)であり、\(1\)と\(4\)以外の約数\(2\)を持っているからです。素数でない数は、合成数（composite number）と呼ばれます。合成数は、いずれかの素数によって割り切れます。

ここでは\(1\)を素数とはしていないことに注意しましょう。なぜかといえば、素因数分解の一意性を保証するものとして都合が良いからです。後で紹介します。

素数について、現在でもまだよくわかっていないことはあります（例えばリーマン予想）。ただし確実にわかっていることもあるわけです。

例えば、素数は限りなくたくさん存在することが知られています。

まず、「無限に存在する」という言葉の意味を明らかにしておきましょう。無限に存在するとは、有限個（例えば\(N\)個）だとすると、\(N+1\)個目の例が存在することです。言い換えれば、有限個であると仮定すると矛盾を導くという意味です。

自然数や整数は、無限に存在します。仮に自然数が有限個だったと仮定しましょう。すべての自然数を\(n_1,\dots, n_N\)と表します。自然数は順序を比較できるので、それらの最大値\(\max\{n_1,\dots, n_N\}\)が存在します。\(K = \max\{n_1,\dots, n_N\}+1\)とすると、\(K\)は自然数に1を加えた数なので自然数ですが、列挙したすべての自然数とは異なる数\(K \neq n_i\)です。これはすべての自然数を\(n_1,\dots, n_N\)と表したことと矛盾しています。よって、自然数が無限に存在することがわかりました。

偶数や奇数も、同様の議論によって無限に存在することが示せます（確かめてみてください）。

素数が無限に存在することを示しましょう。

仮に有限個だとして、\(p_1,\dots,p_N \)をすべての素数とします。それらの積に1加えた数\(P = p_1p_2 \cdots p_N +1\)について考えましょう。\(P\)は素数か、素数でない（合成数）かのいずれかが成り立ちます。場合分けして示しましょう。

\(P\)が素数であると仮定します。すると、整数\(i\)を\(1 \leq i \leq N\)なるものとして、\(P>p_i\)なので、\(P \neq p_i\)です。これは\(p_1,\dots,p_N \)がすべての素数であったという仮定に矛盾します。

\(P\)が合成数であると仮定します。合成数はいずれかの素数によって割り切れるので、\(p_k\)によって割り切れると仮定しましょう。しかし、\(p_k\)は\(p_1p_2 \cdots p_N\)を割り切るので、\(p_k\)で\(P\)を割るとあまりは常に1、割り切れません。これは矛盾です。以上を合わせて、素数が無限に存在することが示せました。

この「素数が無限に存在する」という事実は、古代ギリシャの数学者ユークリッドが「原論」において示したことで有名です。（他の証明方法も知られています）

途中で行った議論を、「\(p_1,\dots,p_N\)を素数とするとき、\(P = p_1p_2 \cdots p_N +1\)は素数である」と解釈しないように注意しましょう。これは一般に間違いです。

例えば、\(N=2\)で、\(3,5\)は素数ですが、\(3\cdot 5 +1=16\)は素数ではありません。\(P\)は素数である可能性も素数でない可能性もあります。（しかし、そのいずれのケースも、素数が有限個だとすると矛盾を導いたわけです）

素因数分解の一意性と応用

正の整数は、必ず素数の積に分解することができます。

例えば、\(204 =2 \cdot 2\cdot3\cdot 17\)、\(1550=2\cdot 5\cdot 151\)といったように。素数それ自身は、ひとつの素数として分解されたものとして考えます。

こうした素数の積への分解を、素因数分解（prime number factorization）と呼びます。素数が整数の理論において重要である理由のひとつは、素因数分解をいつでも行えることが保証されているからです。

素因数分解の一意性（unique prime-factorization theorem）、算術の基本定理（fundamental theorem of arithmetic）

\(x\)を\(2\)以上の整数とする。このとき、有限個の素数\(p_1,\dots,p_N\)により

\[ \begin{aligned}x = p_1 p_2 \cdots p_N\end{aligned} \]

と表せる。積の順序交換を除けば、この表し方は一通りである。

この事実はユークリッドの「原論」の頃から知られたものですが、明確に示されたのは数学者ガウスによる「整数論」と言われています。

\(x\)が合成数だとすると、素数で割り切れるので、それを繰り返せば分解できることが示せます。2通りに素因数分解できたとすると、1つずつ割っていくことで一致することが示せます。証明について詳しくは、「Elementary Number Theory」を参照してください。

素数に\(1\)を含めない理由のひとつは、素因数分解の一意性を保証するためのものです。仮に\(1\)を素数であるとすると、\(204 =2 \cdot 2\cdot3\cdot 17\)で、\(204 =1\cdot 2 \cdot 2\cdot3\cdot 17\)、\(204 =1\cdot 1\cdot 2 \cdot 2\cdot3\cdot 17\)といくらでも別の表し方ができてしまいます。\(1\)はすべての数の約数（自明な約数）なので、積への分解を考えるときには除いておいた方が、本質的に何の積かわかりやすくなります。

素因数分解の応用のひとつは、最大公約数を求めることです。

整数\(x,y\)の最大公約数\(\mathrm{gcd}(x,y)\)を求めるための最も素朴な方法は、\(x,y\)の約数を列挙することです。これは大きな数になってくると面倒です。

もう少し簡単な方法として、（できるなら）素因数分解してみることがあります。

\(\mathrm{gcd}(12,52)\)を求めましょう。\(12 =2 \cdot 2\cdot3\)、\(52=2\cdot 2\cdot 13\)と素因数分解できます。公約数には\(1\)、\(2\)、\(2\cdot 2=4\)があり、その最大のものは\(\mathrm{gcd}(12,52)=4\)です。

\(\mathrm{gcd}(204,1550)\)を求めましょう。\(204 =2 \cdot 2\cdot3\cdot 17\)、\(1550=2\cdot 5\cdot 151\)と素因数分解できます。公約数は\(1,2\)のみなので、\(\mathrm{gcd}(204,1550)=2\)です。

（中学で学ぶ）多項式の因数分解でも、素因数分解を知っていると簡単にできることがあります。

素因数分解を大きな整数に対して行うのは、必ず可能ですが、実際にはかなり難しいです。コンピュータで計算しようとしても、非現実的な時間がかかります。そのことは文字を暗号化する暗号理論（cryptography）に応用されています（例えばRSA暗号）。

数学者のガウスは、整数\(x,y\)を使って\(x+yi\)と表せる複素数が、整数のような性質を持つこと（ガウス整数）を発見しました。このような広い意味での整数を調べる分野は、代数的整数論（algebraic integer theory）と呼ばれています。

整数のもつ代数的な性質を取り出した対象は、抽象代数学では環（かん ring）と呼ばれています。環においては素数の類似として素元というものを考えることができますが、すべての環において素元分解の一意性が成り立つわけではありません。一意に素元分解できる性質を持つ環は、一意分解整域（unique unique factorization domain;UFD）と呼ばれています。

つまり、整数に似た性質を持つ「数」を考えても、一意に「素因数分解」できない例があるのです。このような広い観点から見れば、整数が一意に素因数分解できるというのは、良い性質であると言えます。

以上、素数の性質として、無限にあること、素因数分解の可能性・一意性を紹介し、その応用として最大公約数の求め方を紹介しました。

最大公約数を求めたいが素因数分解が難しい場合でも、ユークリッドの互除法と呼ばれる方法によって求められます（別記事で紹介予定）。

素数は簡単な定義の割に、今なお知られざる性質を持つ対象です。しかし、よく知られた重要な性質として素因数分解が一意にできることがある、ということを知ってもらえたら嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。