どうも、木村(@kimu3_slime)です。
今回は、論理学における「演繹的・帰納的」な推論の違いを、具体例を交えて詳しく解説していきたいと思います。
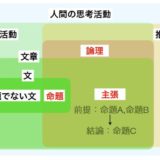
推論について:論理学の考え方、命題、主張、仮定、結論とは何か?
そもそも推論とは何か
「演繹と帰納、どっちがどっちだっけ?」そうならないためにまず大事なのは、演繹・帰納というキーワードだけを覚えないことだと思います。
一般には、演繹法、帰納法と言いますが、それは演繹的な推論、帰納的な推論を略したものです。
推論(argument)とは、簡単に言えば、理由をつけて考えることです。特に、いくつかの前提(premise)から結論(conclusion)を導くことを推論と呼びます。この枠組み自体は、演繹であっても帰納であっても同じです。推論は、主張、論証とも呼ばれます。広い意味では、決断や判断と言っても良いでしょう。
スイロンというと何だか難しく聞こえますが、何かを推測したり予想したりするのは、日常的にやっていることです。
今日はとっても楽しかったね。明日はもっと楽しくなるよね、ハム太郎!
引用:河井リツ子「とっとこハム太郎(アニメ)」
例えば上の文は推論です。前提が「今日はとっても楽しかった」、結論は「明日はもっと楽しくなる」です。
きっと、今日は楽しかったと言えることが、いくつもあったのでしょう。だから、明日も同じように、あるいはそれ以上に、楽しいことがたくさんあるだろうと考えています。単なる推論ではなく、そこには「明日は楽しくあってほしい」という希望も合わさっていますね。
悲しいことに、実際には、今日はとても楽しかったけれど、その次の日楽しくなかった、ということもあるでしょう。前提が正しいにもかかわらず、結論が間違っていることもある。
この推論は、多くの場合では正しい前提から正しい結論を導きますが、必ず正しい結論が導かれるわけではないようです。
演繹的な推論と帰納的な推論
定義
推論は、前提と結論の結びつきの強さによって2種類に分類されます。
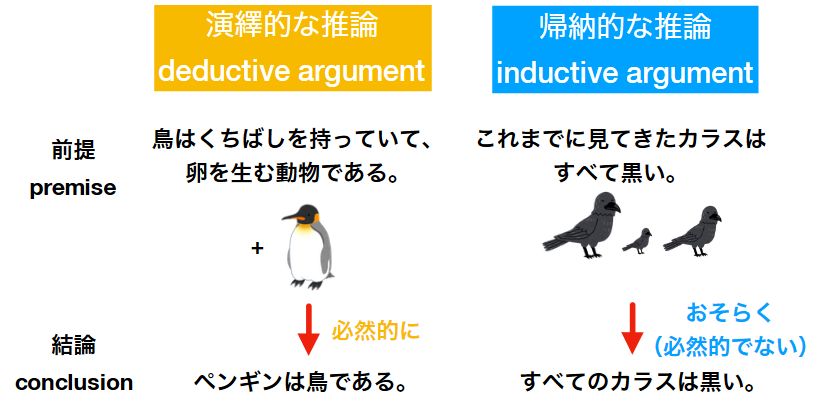
演繹的な推論(deductive argument)は、前提から必然的に結論が導かれるような推論のことです。理論的な推論。
帰納的な推論(inductive argument)は、前提から結論を導くものですが、それが絶対とは言い切れない推論のことです。経験的・感覚的な推論。
帰納的な推論:今までに見てきたカラスはすべて黒い。だから、すべてのカラスは黒い。
演繹的な推論:ペンギンは鳥である。なぜならば、鳥はくちばしを持っていて、卵を生む動物である。ペンギンは確かに動物で、くちばしを持ち卵を生む。
キノウとエンエキ、どちらも難しい日本語です。inductionとdeductionと理解した方がわかりやすいのではないでしょうか。
induceの意味は「説得したり誘発する」ことで、deduceは「推定する、論証する」もの。inductionは、外で見聞きした出来事から自分の内側へ導くイメージ。deduceは、既に知っていることから自分の外側へ導くイメージと。
例
私はゲームでガチャを引いたが、欲しいアイテムに限って引くことができない。このガチャには、引く人の物欲を検知するセンサー(物欲センサー)があるに違いない。
これは帰納的な推論です。実際には、そんなセンサーはないでしょう(あったらすごい!)。帰納的な考え方は、いくつかの観察例をもとに仮説を作ることに役立ちます。経験的な法則とも言えるでしょう。
一方、次の推論は演繹的です。
誰もが欲しいアイテムのレア度は高い。そうしたレアアイテムのガチャにおける排出確率は、低く設定されている。よって、ある人が欲しいアイテムをガチャで引ける確率は、低い。
もし前提が正しいならば、必ず結論が正しいと言えます。明確な出発点をもとに理論を作ることに役立ちます。理論的な法則とも言えるでしょう。
学問における帰納と演繹
帰納的な推論は、理論が確立していない状況で、それでももっともらしく結論を導くのに役立ちます。
伝染病の拡大を防ぐために、帰納的な推論が行われています。コレラという伝染病は、19世紀当時、原因が定かではありませんでした。
ジョン・スノウという医師は、コレラ患者に関する生活状況のデータを集め、「使っている水道会社の違いによって感染する割合が大きく変わるのではないか」と推論しました。これは帰納的なものです。そして、「実際に特定の水道会社の水を使うのを止める」という方法を実行したら、実際にコレラ患者は減りました。
真の原因がわからなくても、100%確実な根拠がなくても、帰納的な推論は役立ちます。ジョン・スノウは、集団を対象とする病気の対策の研究、疫学の父と呼ばれています。彼が取っているのは、データをもとに何が病気の有無に大きく影響する要因なのかを調べることで、統計的なものです。
統計学は、帰納的な考え方を、それがどれだけの確率で間違いうるかを研究していると言えるでしょう。統計学の理論自体は演繹的ですが、それが対象にしているのはデータをもとにした帰納的な考え方です。
一方、数学や論理学は、演繹的な推論を重視します。不確実な帰納的な推論を使わずに、演繹のみから正しいと言える事実を探そうとするわけです。オイラーの多面体定理は、演繹的な推論です。
多面体(複数の平面によって囲まれる図形)において、頂点の数を \(V\)、辺の数を \(E\)、面の数を\(F\)とおくと、
\[ \begin{aligned}V−E+F=2\end{aligned} \]
が成立する。
ここから、頂点が4つ、辺が6つの多面体は、4面体であると言えます。なぜなら、オイラーの多面体定理より、\(F=2-V+E=2-4+6=4\)だからです。これも演繹的な推論です。
演繹的な推論は「前提から必然的に結論が導かれる」と定義しましたが、これはより詳細に言えば、その必然性を明解に説明する証明があるということです。
論理学は推論を調べる学問だという話をしましたが、狭義には、演繹的な推論のみを扱います。演繹的な推論において働く規則を調べる記号論理学、数学の論理学的な基礎を作る数理論理学がそうです。
多くの科学の分野では、演繹と帰納の両方を用いています。
物理学者のアインシュタインは、力学と電磁気学をもとに、相対性理論を導きました。特に、あまりに重力が強くて光さえ脱出できない天体、ブラックホールの存在を予言したと言われています。
実際、2019年、電波望遠鏡によってブラックホールが観測されました。これは演繹的な考え方が役立った例と言えるでしょう。
また、天体運動によるケプラーの法則は、ティコ・ブラーエの観測結果をベースにした推測で、帰納的な推論です。ニュートンは、ケプラーの法則に対応するようにより一般的な法則、万有引力の法則を導きました。万有引力の法則からケプラーの法則を導出するのは、演繹的な推論です。
帰納と演繹という言葉に馴染みがないならば、理論と実験・経験と言い換えても良いのではないでしょうか。演繹とは理論的な推論で、帰納とは経験的な推論です。
(厳密に言えば、すべての帰納法が経験的であるわけではありません。「似ている作りの車は、似た性能をしている」。これは類似、アナロジー analogy による推論と言われる帰納的な推論です。)
演繹的な推論と帰納的な推論の違い
演繹的な推論と帰納的な推論の定義、例を紹介しました。両者の違いは何なのでしょうか?
それは、前提と結論の結びつきの強さの違いです。帰納的な推論では、新たな前提が加わることによって結論の真偽が変わりうるのです。
これまでに見てきたカラスはすべて黒い。だから、すべてのカラスは黒い。
この結論は、白いカラス、アルビノのカラスが存在すれば誤りです。
一方で、演繹的な推論は新たな根拠がいくら加わっても、結論の正しさは変わりません。
すべてのカラスが黒く、かつオイラーの多面体定理の前提が成り立つならば、オイラーの多面体定理は成り立つ。
は正しいです。「すべてのカラスが黒く」の部分をどう変えようが、正しいと言えます。
逆に言えば、前提が正しいときに常に偽を導くような演繹的推論は、常に偽を導きます。(こういう演繹的推論を、妥当でない推論 invalid argument という)
あるカラスが白いならば、\(1=2\)である。
これは前提は正しいですが、(\(1\neq 2\)となる普通の数を考えるとして)結論は誤りです。前提を変えたり、あるいは増やしたりしても、「\(1=2\)である。」という結論は偽です。
これが前提と結論の結びつきが強いということの意味です。演繹的な推論では、前提と結論は密接な関係にあって、いくら外から前提を崩そうとしても崩れません。一方、帰納的な推論は、ゆるさのある推論で、新しい前提が加わって結論が崩れることがありえます。
確率的な推論と演繹・帰納の関係
前提と結論の間の「必然性」「確実さ」という話をしましたが、「100%正しい=演繹的」「確率的に正しい=演繹的」と考えるのは、イメージとしては良いですが、厳密に言えば間違いです。
確率の捉え方にも、演繹的なものと帰納的なものがあります。
帰納的な推論:このガチャは1%の確率で当たりが出るとメーカーは言っているが、200回やって1回も当たりが出なかった。メーカーは嘘をついているのではないか。
演繹的な推論:1%の確率で表があるコインがあるとする。100回コインを投げたとき、1回も表が出ない確率は\( (0.99)^{200}\)で、約13%である。
「200回やって1回も当たりが出なかった」という状況での確率は、\(0/200\)、すなわち\(0\)です。これは頻度にもとづく確率、経験的な確率と呼ばれます。
「1%の確率で表があるコイン」というときの確率は、場合の数を考えて計算したもので、理論的な確率、数学的な確率と呼ばれます。頻度をものすごく大きく、サンプルをものすごく大量に取ったときに近づく頻度的な確率の値を見て、理論的な確率を定めているわけです。数学における確率論の分野における「確率」という言葉は、理論的な確率を指しています。
確率を使った推論でも、演繹的な推論と帰納的な推論があり、一概にどちらかと言えるわけではないことに注意しましょう。
まとめ
演繹的な推論、帰納的な推論の定義、例、違いなどを紹介してきました。
両者は、前提から結論を導くという推論である点については一致しています。違うのは、前提と結論の結びつきの強さです。
どうやっても結びつきが崩れないのが、演繹的な推論です。概ね正しそうだけれど、新たな前提によって結論が間違いとなりうるのが、帰納的な推論です。
演繹的な推論には確実さというメリットがあり、帰納的な推論には経験をもとに推論ができるというメリットがあります。帰納的だから良い、演繹的だから良いという話ではなく、推論は使いよう、というわけですね。
論理学は、どちらかというと演繹的な推論を扱う学問です。論理の文脈で推論というとき、演繹的であることが半ば暗黙のものとなっていることすらあります。しかしそこには、帰納的な推論を含む日常的な推論との違い、制限があるのです。そのことが、今回の話で伝わったら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Introduction to Logic (English Edition)
参考文献
Copi, Cohen, MacMahon “Introduction to Logic”