論理学の考え方、命題、主張、仮定、結論とは何か？

どうも、木村（@kimu3_slime）です。

今回は、そもそも論理学の考え方や意義はどういうものなのか、命題、主張、仮定、結論とは何かといった基本概念を、身近な具体例を交えて、詳しく紹介します。

論理とは何か：人の推論能力
- 論理を使わない推論
- 論理への通俗的な誤解
論理の基本単位：命題
推論の方法：主張、仮定、結論
参考文献
こちらもおすすめ

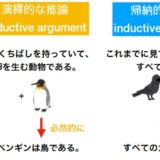
論理とは何か：人の推論能力

人間には、過去の経験や知識をもとにして、未来のことを考える力があります。空が暗くなるほどに曇ってきたとき、雨宿りできる場所を探そうと考えるでしょう。多くの出来事には原因がある、つまり原因が結果をもたらすという考え方は古くから知られ、仏教では因果と呼ばれています。では、昔から言われる、「なまずが暴れると地震が起こる」は本当なのでしょうか？

論理学（logic）は、ものごとに理由（reason）をつけて考える方法を調べます。特に、正しい推論（inference）と正しくない推論を見分ける原理を与えてくれます。論理学は推論を扱う学問です。

「なまずが暴れるとき、地震が起こる」という文のように、何かが正しいと述べることを、論理学では主張（argument）と呼びます。誰でも「星は地球の周りを回っている」と言えるように、主張すること自体はどんな人間でも可能です。しかし、その主張が正しいと人を納得させるのは、誰でもができることではありません。「その主張は、適切な理由や根拠にもとづくものか？」と考えるのが、論理的な態度ではないでしょうか。

論理を使わない推論

人間は、何もかもを論理的に考えているわけではありません。理由をつけて正しいと思われる主張だけが、受け入れられているわけではない。いわば、非論理的な部分があります。

古代ギリシャの哲学者のプラトンは、「徳を教える」と言いながらも「徳とは何か」を問題にしない言論家・ソフィストを批判しました。自信なさそうに話しているより、動じずに堂々と話ている人の話の方が信用されやすいですが、これはレトリック（弁論術）と呼ばれる技術で、政治的なスピーチに利用されています。本来、言っていることが正しいかどうかと、話し方には関係がないはずです。しかしながら、人は心地良い話を受け入れ、都合の悪い結論を受け入れたがらない傾向にあり、心情的（emotional）に判断を下すことがあります。

また、偉い人が言っていることは正しいと考えられる傾向にあります。年長者が言ってるから、先生が言ってるから、政治家が言ってるから、社長が言ってるから、海外が言ってるから。これらは、権威（authority）に訴える方法です。昔からそうだから（習慣 habit）、みんながそう言ってるから（同調 sympathy）、イメージ的にもっともらしい（比喩 metaphor）という考え方もありますね。

心情、権威、習慣、同調、比喩、それを使うこと自体は悪いことではありません。素早く決断を下したり、グループにおける協力状態を維持したりするのに役立つでしょう。しかし、「主張が正しいかどうか？」を考えるには、それらは理由として弱く、確実な推論ができるか怪しいものです（「地球は回っていた」のです）。そうした不確実さを排除した推論が、論理学の領分となります。

論理への通俗的な誤解

日本において、論理学への理解と教育が不足していると僕は考えています。論理学の考え方は、政治について適切に議論して合意形成する基盤となり、民主主義社会の支えです。また学術、科学といった、目に見えないものや概念について、確実な知識を記述するための言語の役割も果たしています。多くの人の役に立つものです。

しばしば、論理という言葉が、非創造的、非情緒的、機械的、非人間的というような意味で使われるのを耳にします。それらは、必ずしも論理と相反するものではありません。

ダイヤモンド・オンライン「日本が新たな需要を生めなくなった一因は「論理偏重」だ」や、ほぼ日刊イトイ新聞「論理と情緒」などは、「論理」という言葉を用いてはいますが、これは単に経済合理性を意味しています。習慣などの社会的な合理性は、「正しさ（がすべてじゃない）」といったように言われます。しかし、合理的であることと論理的であることは、一般には別物です。すべての合理的な活動が、論理的に説明できるとは限りません。論理学の目的は正しい推論の探求であり、利益を上げることや効率性ではありません。

また、「論理的である＝正しい」と考えるのは、適切ではありません。それこそ、論理の飛躍があります（笑）。普通の人が「論理的である」と感じるとき、それは「論理的っぽい」と感じるだけであって、実際その議論が論理に即した、確実な根拠を持ったものとは限りません。論理学は、推論が正しいか正しくないかを判別することを重視します。つまり、何の事実が正しく何が正しくないかを判定してくれるわけではないのです。たとえ推論が正しくとも、出発点となる仮定が間違いならば、導かれる結論は間違いです。あくまで、いくつかの事実から結論を導く過程・プロセスが正しいかどうかが、論理学の対象となっています。

なので、ある人たちの間で「論理的に正しい」とされたことであっても、前提としている仮定が違えば、結論は誤りとなりえます。論理を使えばすなわち正しいとは言えず、必ずしも万人にとっての正しさを導くわけではありません。

このように、論理学は万能ではありません。あくまで、真偽の探求という目的において、理由をつけて真偽を導く技術、論理は有効だと思っています。逆に、誰もが納得できる推論をする方法で、論理以上に確実なものがほかにあるならば、教えていただきたいものですね。

文化人類学者のホールは、世界中の言語コミュニケーションをハイコンテクスト文化とローコンテクスト文化に分類しました。日本語は、言葉にされないコミュニケーションや前提が多く、ハイコンテクスト文化とされています（この用語自体に実証的な根拠があるかはともかく……）。

せっかく学校で何かを学び知識をつけるならば、「察し」だけに頼らない議論とコミュニケーションの技術であり、知的生産の基盤である、論理学を身につけておきたいものですね。

論理の基本単位：命題

論理学は、主張の理由付け、推論が正しいかどうかを問題にするという話をしました。

では、確実に言えることをどうやって見つけたら良いでしょうか。一般に、複雑な文章が正しいかどうかを判別するのは難しいですよね。逆に言えば、単純な文章を分解パーツとして使うのが、思考の過程を追うには良さそうです。

その基本単位は、命題（proposition）と呼ばれます。命題とは、正しいか間違っているか(true or false)が明らかに定まっている文（sentence）のことです。命題は、ステートメント（statement）とも呼ばれます。

命題である文：今日は晴れている。
命題である文：念仏さえ唱えていれば、極楽浄土に行ける。
命題でない文：ありがとうございます。
命題でない文：帰ったら、手を洗いなさい。
命題でない文：将棋の遊び方を知ってるか？

人間の思考の過程は、一般には他者から目に見えないものです。しかし、会話や文章などの言語活動は分析できます。声は文章化できるので、文章の最小単位である文を扱います。文であっても、正しいとも間違っているとも言い難いものは推論に関しては使えません。なので、命題だけ扱うわけです。

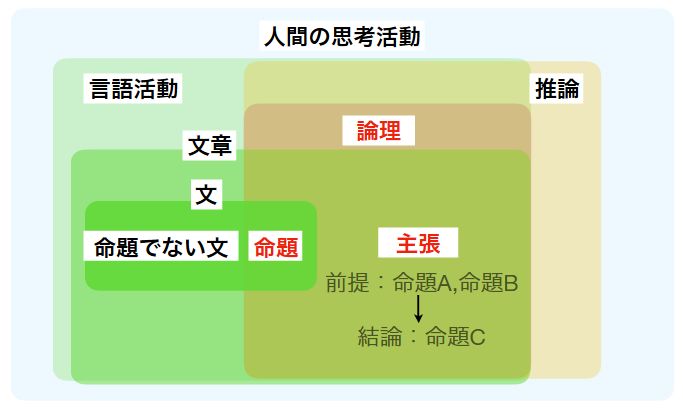
命題：このりんごは赤い
否定命題：このりんごは赤くない

「このりんごは赤い」が正しいとき、「このりんごは赤くない」は誤りと考えます。どのような命題Aを考えても、AまたはAの否定命題のいずれかは正しいです。これを排中律（law of excluded middle）と呼びます。

「このりんごは赤くて、かつ赤くない。このりんごは赤緑だ。」と日常的には、考えることもあるでしょう。しかし通常の論理学では、命題と言えば「真か偽かいずれかである」文を指しています。このような立場は、二値論理学(two-valued logic)、古典論理(classical logic)、標準論理(standard logic)と呼ばれるものです。

日常的な会話や思考と、論理学における命題の世界には、少しギャップがあります。

この文は命題か？：日本人は勤勉である。

この文は、このままでは命題であるとは言い難いです。「勤勉である」ことの意味、つまり言葉の定義が、多義的で曖昧だからです。「勤勉であること＝1日10時間である」とすれば誤りの文で、「勤勉であること＝1日1回は呼吸をする」とすれば（無茶がありますが）正しい文となります。つまり、文の意味を明解にしなければ、命題として扱うのは難しいです。もし、「日本人」「勤勉である」ことの定義が明解に与えられれば、命題として扱えるでしょう。

次の文では、文の意味と意図にずれが生じています。

文1：（私）なんで怒ってるかわかる？
文2：お腹すいたなあ

文1に対し「あなたが怒っているのは、理由Aのためである」と返しても、相手は満足しないかもしれません。それは推測した理由Aが間違っているときだけでなく、たとえ理由が合っていてもそうです。理由を答えてほしいのではなく、「謝ってほしい」「なぐさめてほしい」という要求の可能性があります。

友達に文2を言われたときに、「友達はお腹が空いている」と捉えるのは間違いではありません。しかしそこには、「お腹が空いた、だからご飯へ出かけよう」「お腹が空いた、だからご飯を買ってくる」といった意図が隠されているかもしれません。

普通のコミュニケーションには、真偽の世界（論理）で捉えられる部分と、そうでない部分が混じっています。

論理学では、真偽で捉えられる部分を探そうとします。もしそうでない部分があったら、その定義や文脈を明解にし、確かな意味を持たせることも必要になるでしょう。

すべての文が、論理学の対象である命題になるわけではありません。そのことは、論理学の価値を下げるわけではありません。ただ、有効な範囲、限界があるということです。その上で、多くの命題・主張に当てはまる理由付けの法則を探すのが、論理学の目的となっています。

推論の方法：主張、仮定、結論

論理学の基本単位は、命題であるという話をしました。文を命題と呼ぶとき、真偽のいずれか定まる形でありさえすれば良く、実際に正しいか間違っているかがわからなくても良いです。真偽が未知な命題に対しては、「この命題は正しいか？」と問うことができます。

ある命題が正しいことを、他の命題の正しさから導く過程が、命題のが正しいことの理由付け、すなわち推論です。

それは、主張、論証、推論（argument）（特に論理的な主張 logical argument）と呼ばれます。主張とは、「そのうちのいくつかの命題によって、ある命題が示されるような命題の集まり」と定義します。

主張は、単なる命題の集まりではありません。そこには、スタートとゴール、前提と結論があります。主張の結論(conclusion)とは、主張の他の命題をもとにして確かめられる命題のこと。前提(premise)とは、結論を導くために使われる命題のこと。前提は、根拠、仮定とも呼ばれます。

主張の例を見てみましょう。

ぼくらはみんな生きている生きているから歌うんだ
引用：「手のひらを太陽に」やなせたかし

これは主張として見ることができます。「ぼくらはみんな生きている」と「（ぼくらは）歌うんだ」という2つの命題がありますね。そして、結論は「（ぼくらは）歌うんだ」で、前提は「ぼくらはみんな生きている」ですね。

　十日ほどたって、ごんが、弥助（やすけ）というお百姓の家のうらをとおりかかりますと、そこの、いちじくの木のかげで、弥助の家内（かない）が、おはぐろを付けていました。かじ屋の新兵衛（しんべえ）の家のうらをとおると、新兵衛の家内が、かみをすいていました。ごんは、「ふふん。村に何かあるんだな。」と思いました。
引用：「ごんぎつね」新美南吉

これは主張です。結論は、「村に何かある」こと。その前提は、「弥助の家内が、おはぐろを付けていた」「新兵衛の家内が、かみをすいていた」ことですね。

全部は紹介しませんが、ごんはこの後も順番に推論を行っています。「村で何かがある」→「村で葬式がある」→「兵十の家で葬式がある」→「兵十の家の誰かが死んだ」→「死んだのは兵十のおっ母だ」と。そのひとつひとつをとっても、前提から結論を導いています。ぜひ、前提と結論の関係を原文から見出してみてください。

結論が先に述べられるケースもあります。

Good sense is, of all things in the world, the most equally distributed, for everybody thinks himself so abundantly provided with it that even those most difficult to please in all other matters do not commonly desire more of it than they already posses.
良識（理性）は、この世で最も公平に分配されているものである、というのは、誰でもそれを十分に与えられていると思っているので、他の全てのことではめったに満足しない人々でさえも、良識については、自分が持っている以上を望まないのが普通だからである。
引用：René Descartes, Discourse on the Method of Rightly Conducting the Reason, and Seeking Truth in the Sciences ルネ・デカルト『方法序説』

結論は、「良識（理性）は、この世で最も公平に分配されているものである」。前提は、forより後の文、「誰でもそれを十分に与えられていると思っているので、他の全てのことではめったに満足しない人々でさえも、良識については、自分が持っている以上を望まないのが普通だ」ですね。

詩的な文章であっても、そこにはもっともらしい思考の過程、論理が見られることがあります。