どうも、木村(@kimu3_slime)です。
以前記事で紹介した生物の模様に数式が関わっている話には、微分方程式(びぶんほうていしき)という数学が使われています。
微分方程式は、何かの「動き」を説明します。この方程式は、高校で習う微分(びぶん)・積分(せきぶん)という概念が基礎となっています。
微分というのはグラフの接線の傾きを求めること、積分というのはグラフの描く面積を求めること、とよく説明されます。
いや待って、と思いませんか?(僕は思います) なんでグラフの接線を求めたり、面積を求める必要があるのか。それがイメージできずに微積分が「できる」ようになってもしょうがない。
今回は、「運動」をビジュアルイメージとして使い、微分と積分を中学生レベルでもわかるように説明していきます。
カーリングというシンプルな運動
まず、一番シンプルな運動として、カーリングをイメージしましょう。
一度投げた石は、止まらずに一定速度で進み続けるような動きをするでしょう(現実では、摩擦があるので止まりますが)。
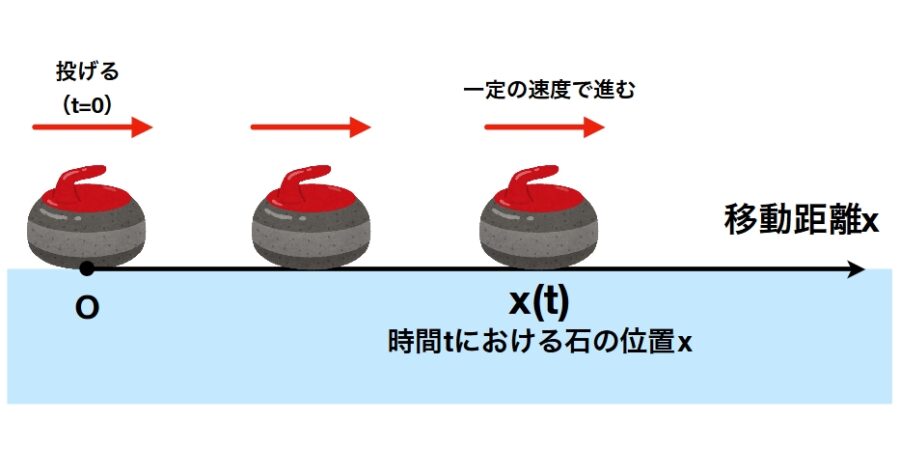
このときの石の位置と時間の関係を調べてみます。
知りたい位置(メートル)を未知数の\(x\)、時間(秒)をtimeの\(t\)と文字で表すことにしましょう。
この運動において、\(x\)と\(t\)との間には何か関係があります。これを時間\(t\)における位置\(x\)を\(x(t)\)と表記することにします。
例えば、2秒後に4メートルの位置にあるような運動を考えましょう。つまり、\(x(2)=4\)です。この運動において石は一定の速さで動きますから、倍の時間が経てば\(x(4)=8\)となるでしょう。より一般的に言えば、\(x(t)=2t\)という関係式が成立しています。
位置と時間は対応関係\(x(t)\)にあります。これを位置\(x\)は時間\(t\)の関数、\(x\)は\(t\)を変数とする関数であると言います。よりシンプルに、位置関数と呼びましょう。
さて、この位置関数から速度を求めることはできないでしょうか。そこで役に立つのが微分です。微分とは、微小な変化を取り出す操作です。
速度をvelocityの\(v\)で表記します。速度もまた時間の関数なので、\(v(t)\)と書きましょう。
小学校では、速度=位置/時間で求められると教えられます(いわゆるみはじ、はじき)。つまり、\(v=x/t\)というわけです。
しかし、厳密に言えば違うのです(笑)(このケースでは問題なく計算できますが)。「速度=位置を時間で微分したもの」が正しい定義です。これを\(v=dx/dt\)と書きます。dは微分(differentiation)のdです。
速度は位置の(単位時間あたりの)変化率。これを速度関数は位置関数の微分である、とも言います。
このケースでは、速度を求めるのは簡単です。時間によらず一定の\(v(t)=2\)ですね。グラフに表すとこうです。
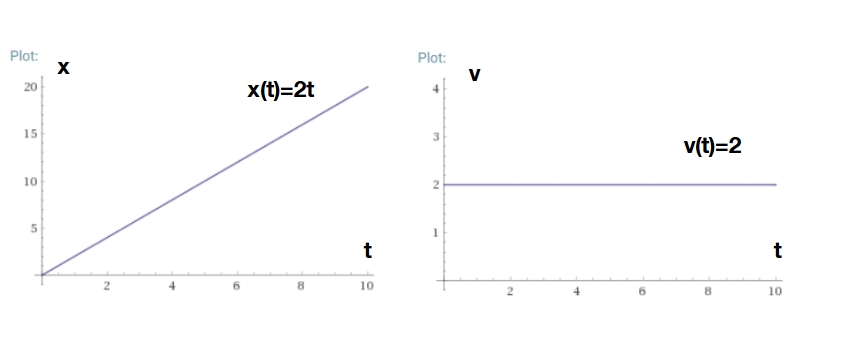
このように一定の速度で動く運動を、等速直線運動と言います。
同じように、\(x(t)=at\)(\(a\)は時間によらない定数)という位置関数を考えても同じことができますよね。このときは\(v(t)=a\)となります。
速度は位置関数の傾き\(a\)と一致しています。これが微分が(接線の)傾きを取り出すということの意味ですね。
今度は、位置関数がわからないとき、移動距離について調べてみましょう。
速度関数がわかっていれば、移動距離は計算できるのです。
今回は、速度が一定値である、例えば\(v(t)=2\)であったとしましょう。
移動距離を求めるときに使えるのが積分です。移動距離を細かく足し合わせていけば良い、という話です。
例えば、時間\(t\)までに移動した距離を\(S(t)\)とします。
小学校では、距離=速度×時間と習います。つまり、\(S=vt\)です。
より厳密には、移動距離=速度関数の時間に関する積分として定義されます。
これは
\[ \begin{aligned}S(t)=\int ^t _0 v(t)dt\end{aligned} \]
と表されます。
右辺の意味は、\(v(t)\)が時間\(t\)までに描くグラフの面積を求めなさい、ということです。ニョロン\(\int\)という記号(インテグラル)の意味はわからなくていいです。
\(t=8\)だとしたら、どれだけ移動したでしょうか。秒速2mで8秒動いたら、\(S=16\)です。これは小学生でもわかりますね。
実は! この移動距離は、距離関数のグラフが描く面積と対応しているのです。
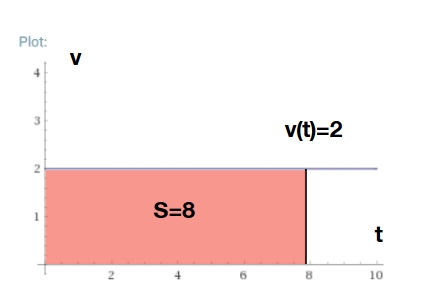
上の図の、グラフによって作られる四角形の面積を求めてみましょう。\(S(8)=\int ^8 _0 2 dt=8\times2=16\)で、さきほどの結果と一致しますね。
これも一般化できます。\(v(t)=a\)(\(a\)は時間によらない定数)として、\(t\)秒後までの移動距離を求めれば\(S=at\)となります。
なんだか当たり前のことをやっている気がしますか?
「位置を時間の関数として表す」ことができたとします。もし微分と積分をマスターしていたら、位置関数から、速度が計算できるのです。つまり、運動の未来予測ができる!
逆に、「速度だけが計測できていた」とします。そのときも、積分をマスターしていたら、移動距離を自由に計算できるわけです。
この関係性は、グラフによってビジュアル化できます。速度は位置関数の(接線の)傾き具合として、移動距離は速度関数のグラフが描く面積として。
カーリングの例はすごくシンプルな運動(等速直線運動)なので、もう少し難しい運動でも考えてみましょう。
ボールを投げると放物運動
今度はカーリングではなく、ボールを空へ投げるとします。
これは経験からわかるように、放物線を描きます。まさに物を放ると描かれる線、まさに放物線です。
位置の関数(高さのみ考える)は、例えば\(x(t)=-(t-2)^2+4\)と表されるでしょう。2秒後に頂点の高さ4メートルに達し、4秒後に元の位置まで落ちてきます。
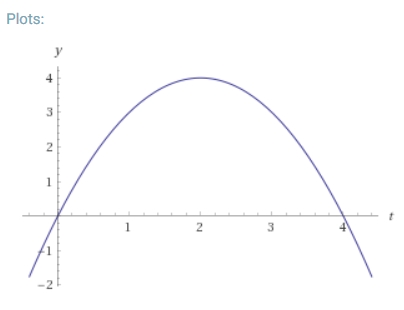
さあ、速度を求めてみましょう。
等速直線運動でなくなると、もう小学生の知識ではどうすればいいのかわらかなくなります。最初上に速い…途中で止まる…最後は下に速い…くらいのイメージですね。
もし微分法を知っていたら、
\[ \begin{aligned}v(t)=\frac{dx(t)}{dt}=-2t+4\end{aligned} \]
と計算できます。
\(v(0)=4\)、\(v(2)=0\)、\(v(3)=-2\)となるわけです。これらは、じつは位置関数のその時刻における接線の傾きと一致します!
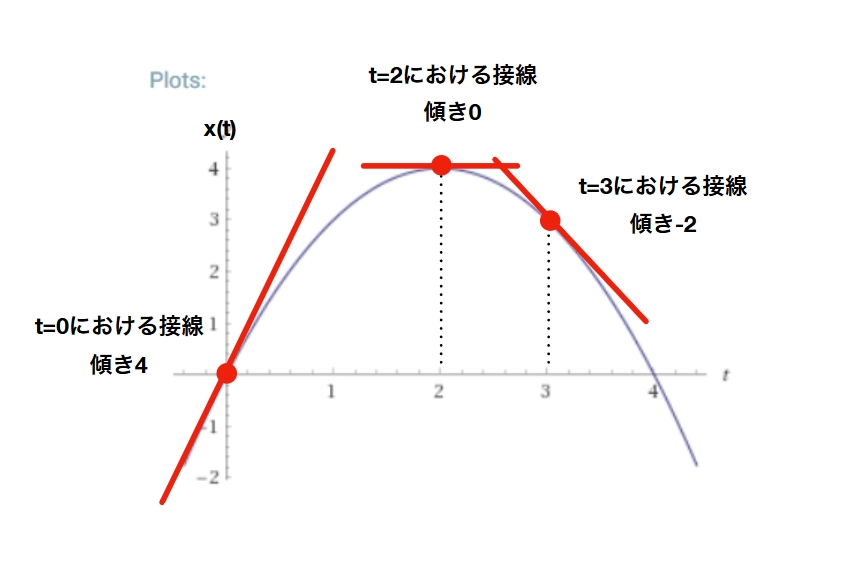
これは偶然ではなく、微分は、もとの関数のグラフから、各点における接線の傾きを取り出す操作として定義されます。数式で言えばこうです。
\[ \begin{aligned}\frac{dx(t)}{dt}:=\lim_{\Delta t \to 0} \frac{x(t+\Delta t)-x(t)}{\Delta t} \end{aligned} \]
詳しくは説明しませんが、こういう意味です。\( \frac{x(t+\Delta t)-x(t)}{\Delta t}\)は、変化率です。微小時間\(\Delta t\)が経過する間に、\(x(t)\)がどれだけ増減したかを示します。微小時間\(\Delta t\)を限りなく小さくしていけば、変化率はやがて傾きと一致するでしょう。
微分は変化の割合を(瞬間的に)求めているだけです。要は割り算です(雑)。
位置の関数は、各時間毎にどれくらい変化してるの? それを求めることが、微分、速度関数の計算です。
今度は、位置関数がわからず、速度関数のみがわかっている(\(v(t)=-2t+4\))としましょう。
そんなときは、積分法を知っていれば、移動距離\(S(t)\)は計算することができます。
例えば\(t=3\)のときは
\[ \begin{aligned}S(3)=\int ^3 _0 -2t+4 dt=[-t^2+4t]^3 _0=3\end{aligned} \]
と求められます。
これは\(v(t)\)のグラフが描く面積(0より下側は引き算として計算する)と一致します。これなら小学生でも計算できる式です。
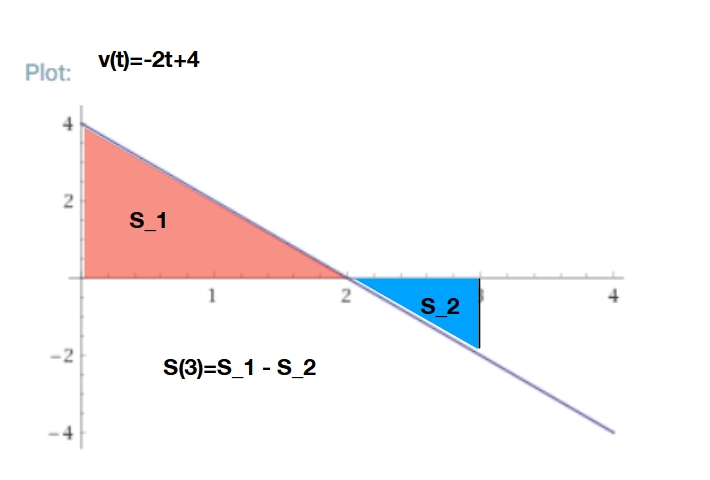
\[ \begin{aligned}S(3)=S_1 – S_2 =2*4/2 – 1*2/2 = 3\end{aligned} \]
となり、さきほどの結果と一致します。
そうです、積分とは、グラフの面積を求めなさい、という計算なのです。定義式はこうなります。
\[ \begin{aligned}\int ^t _0 v(s)ds = \lim _{|\Delta| \to 0} \sum _{\Delta} f(c_k)\cdot(c_k – c_{k-1}) \end{aligned} \]
これは微分より計算しにくい式です。何をしているかというと、グラフを短冊のように切って、細かい長方形の足し合わせとして面積に近いものを求めていくのです。\(f(c_k)\cdot(c_k – c_{k-1})\)というのは、単に長方形の面積の求め方、タテ×ヨコ。\(\sum\)は足し合わせること。そして短冊のように切る分割\(\Delta\)を限りなく細かくしていけば、やがて面積に近づいていきますよね…という話。
積分は、(長方形によって細かく)グラフの面積を求めています。要は足し算です(雑)。
まとめ
なんでグラフの接線を求めたり、面積を求める必要があるのか。
それは、カーリングやボールを投げる運動をイメージすれば、わかりやすいです。
運動を分析するときに出てくるグラフは、位置関数や速度関数です。
位置関数の接線の傾き(微分)からは速度という情報が手に入りますし、速度関数の描くグラフの面積(積分)からは移動距離がわかります。
\[ \begin{aligned}v(t)=\frac{dx(t)}{dt}\end{aligned} \]
\[ \begin{aligned}S(t)=\int ^t _0 v(s)ds \end{aligned} \]
雑に見れば、微分は割り算、積分は足し算です。怖くない。
微分の話は速度を求めるからわかるけど、速度が先にわかっていて……という積分の話は、ちょっと現実的ではなく、疑問かもしれませんね。
これが微分方程式の話につながってきます。微分方程式は、文字通り微分によって表される方程式です。
例えばニュートンの運動方程式は、次のように表されます。
\[ \begin{aligned} m \frac{d^2 x(t)}{dt^2} = F\end{aligned} \]
\(m\)は物体の質量、\(F\)はかかっている力、位置を二回微分したもの、すなわち速度の微分\(a := \frac{dv(t)}{dt}=\frac{d^2 x(t)}{dt^2}\)は加速度(acceleration)と呼ばれます。
\(m,F\)がわかっているときに、この方程式を満たす位置関数\(x(t)\)は何かを求めること。それが運動方程式を解くということです。
しかし、二回微分が含まれる式を解くのは、難しいです。なぜかといえば、\(x(t)\)がどんな形の関数なのか予想しにくいからです。あれやこれやと当てずっぽをするのは困難です。
そこで微分方程式を解くために、実は積分法が使えて(微積分学の基本定理)……という話は、またの機会に。
木村すらいむ(@kimu3_slime)でした。ではでは。